0. Intro

---

지난 포스트에서는 "사용하는 활성화 함수에 따라 신경망의 종류가 나뉜다."고 했습니다.

이번 포스트에서는 대표적인 퍼셉트론 (perceptron), 로지스틱 회귀 (logistic regression), 소프트맥스 회귀 (softmax regression)에 대해 알아보겠습니다.

공부 소스 : 혁펜하임의 "꽂히는" 딥러닝 (Youtube)

1. 회귀 vs 분류

---

• 회귀 (regression) : 데이터가 주어졌을 때 모델과 가장 가까워지도록, 즉 오차 (error)가 작아지도록 가중치 (weight)를 수정하는 것
• 분류 (classification) : 주어진 데이터들을 토대로 class를 나누는 것. 즉, 데이터의 특징을 기반으로 그룹을 형성하는 것

2. 퍼셉트론 (Perceptron)

---

퍼셉트론은 single layer NN이며, 분류 문제에 많이 쓰입니다.

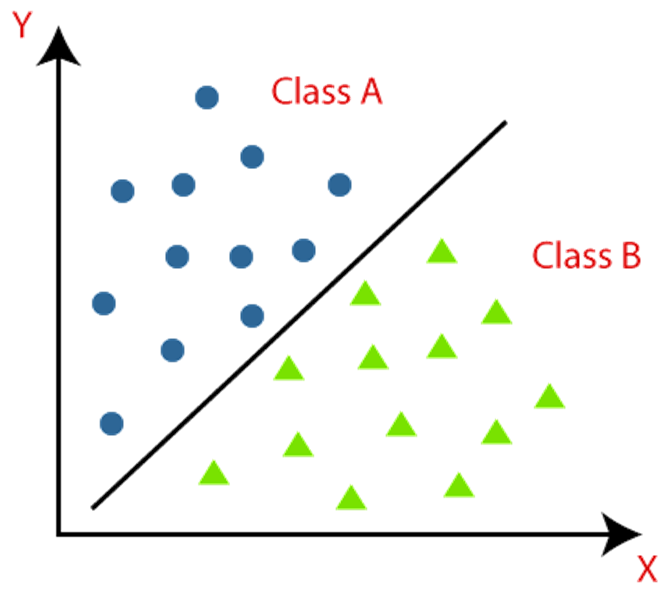출처 : papers with code. "General Classification"

위 그림처럼 직선을 통해 class를 나눌 수 있습니다.
"직선 위에 있으면 class A, 아래에 있으면 class B"

하지만 직선 하나로는 정확한 분류가 불가능하기 때문에 직선 2개를 사용하여 분류하기도 합니다.
"$l_1\geq0 \ \operatorname{and} \ l_2\ge0$ 또는 $l_1\leq 0 \ \operatorname{and} \ l_2\leq 0$이면 class A로 분류한다."

이처럼 AND, OR 연산을 적절히 섞어서 사용하면 더욱 복잡한 분류가 가능합니다.

AND

---

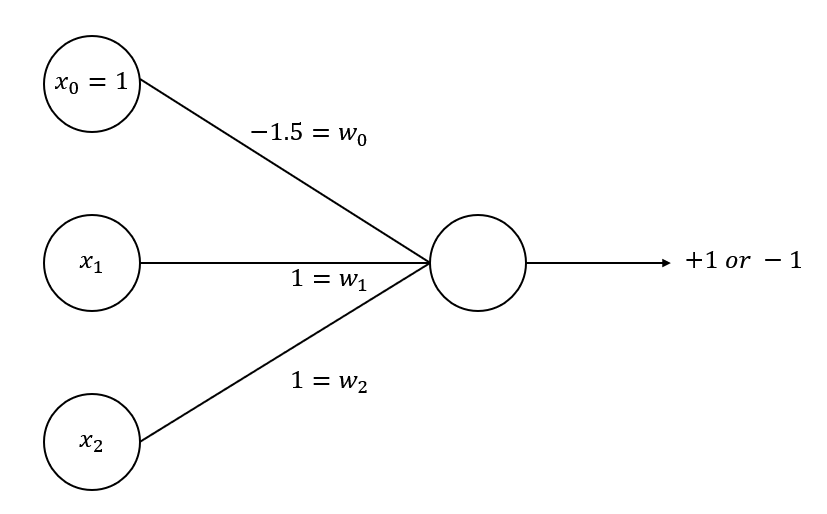
위와 같은 신경망이 있다고 가정합시다.
$x_0,x_1,x_2$에 가중치 $w_0,w_1,w_2$를 곱해서 더한 값이 양수이면 +1, 음수이면 -1을 반환합니다.

이때 $x_1,x_2$의 값은 1 또는 -1만 가능하고, AND 연산을 만들어주기 위해 임의로 가중치를 $w_0=-1.5, w_1=w_2=1$로 지정했습니다.

이렇게 하면 $x_1=x_2=1$인 경우에만 $1\times (-1.5)+1\times 1+1\times 1=+0.5$가 되어 +1을 반환하고, 나머지 경우에는 모두 음수가 되어 -1을 반환합니다.
두 값이 모두 1, true여야만 결과값이 1, true가 나오는 AND 연산과 동일하게 만들어졌습니다.

따라서 이 신경망 (퍼셉트론)은 AND 연산을 가능하게 해주는 퍼셉트론이라고 할 수 있습니다.

OR

---

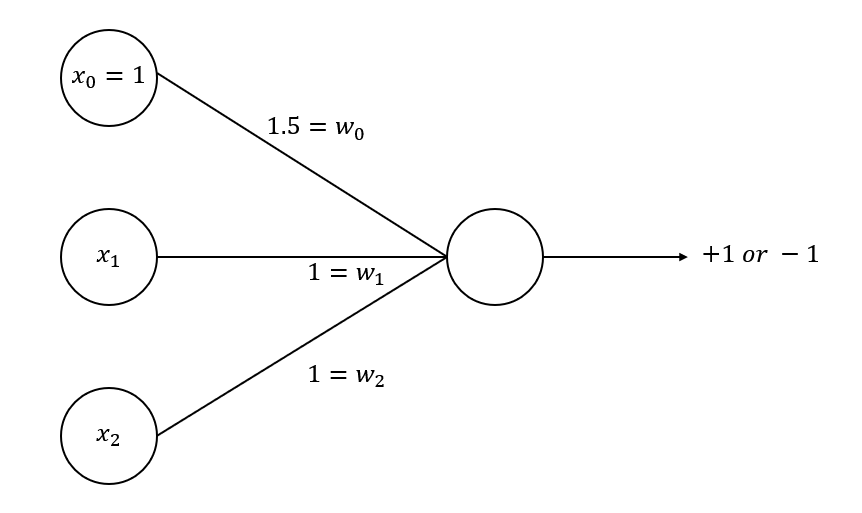
AND 연산과 동일하지만, $w_0$ 가중치만 $1.5$로 수정했습니다.

이렇게 하면 $x_1=x_2=-1$인 경우에만 $1\times 1.5+(-1)\times 1+(-1)\times 1=-0.5$가 되어 -1을 반환하고, 나머지 경우에는 모두 +1을 반환합니다.
두 값 중 하나만 1, true여도 결과값이 1, true가 되는 OR 연산과 동일합니다.

따라서 이 퍼셉트론은 OR 연산을 가능하게 해주는 퍼셉트론입니다.

3. MLP (Multi-Layer Perceptron)

---

아까 말했듯이 퍼셉트론은 single layer NN입니다.
이 구조를 multi-layer로 확장하고, 각 layer를 AND, OR로 연결한 것이 MLP입니다.

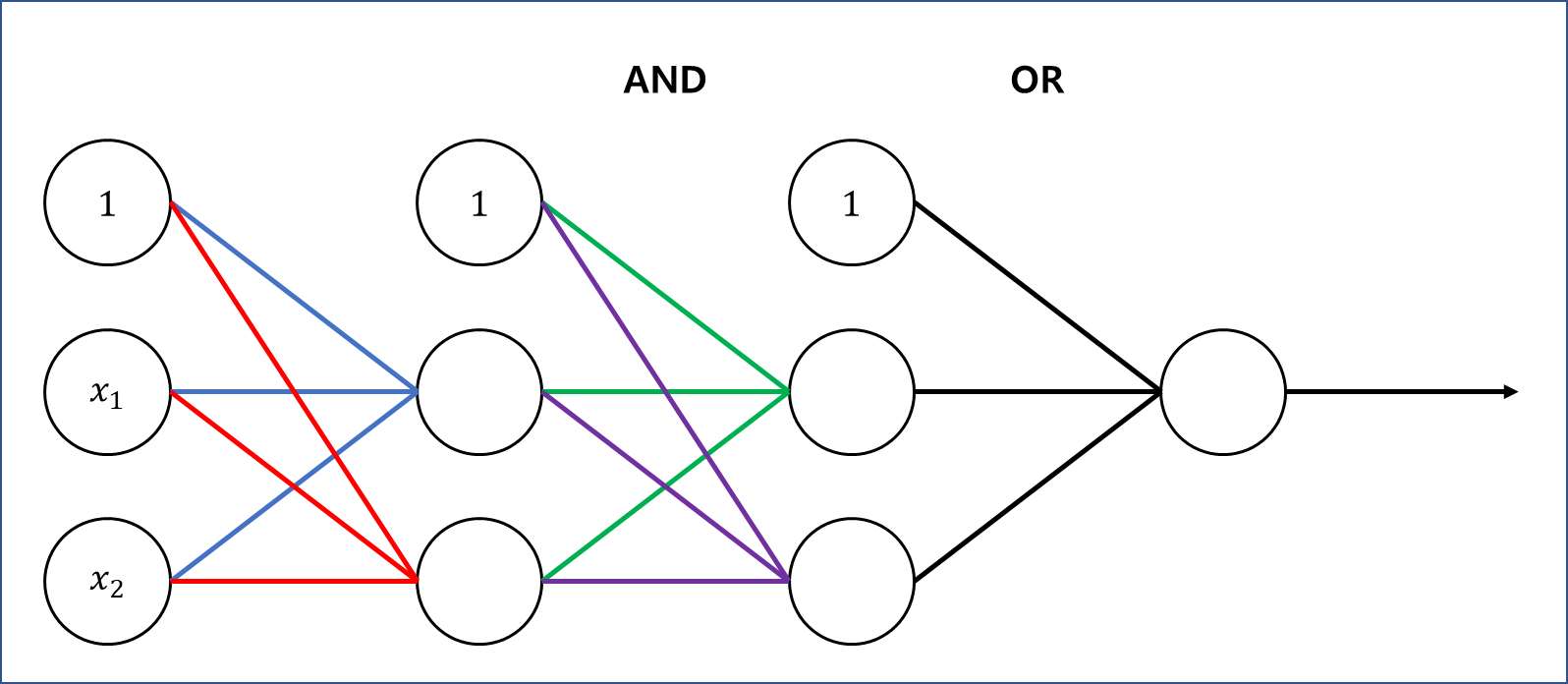
이때 input layer는 직선을 나타내고, 이 때문에 $x_1, x_2$라는 두 개의 벡터가 입력으로 들어옵니다.
가중치를 잘 설정하면 $w_1x+w_2y=constant$ 형태로 직선 $l_1, l_2$를 표현할 수 있습니다.

이렇게 나온 직선들을 AND 연산을 통해 묶어줍니다. (초록색, 보라색 선)
$l_1\geq0 \ \operatorname{and} \ l_2<0$
$l_1<0 \ \operatorname{and} \ l_2\geq 0$

이 결과를 다시 OR 연산으로 묶으면 최종 결과값은 +1 또는 -1이 나올 것이고, 값에 따라 +1과 -1을 다른 class로 분류할 수 있습니다.

MLP에서는 결과값이 +1이 나오도록 가중치를 잘 설정하는 것이 목표입니다.
이때 적절한 가중치를 찾는 것이 machine의 목표입니다. 분류의 형태가 직선이라는 것만 제시해주고, 가중치를 찾는 것은 machine이 수행합니다.

만약 분류에 사용되는 직선이 여러 개라면 (여러 개의 퍼셉트론을 사용한다면) non-linear한 영역까지 분류할 수 있습니다.

4. 로지스틱 회귀 (Logistic Regression)

---

이전 포스트에서 설명했듯이 로지스틱 회귀의 활성화 함수는 시그모이드 함수 (sigmoid function)입니다.
(로지스틱 회귀는 single layer NN입니다)

시그모이드 함수
$y=\frac{e^x}{1+e^x}$

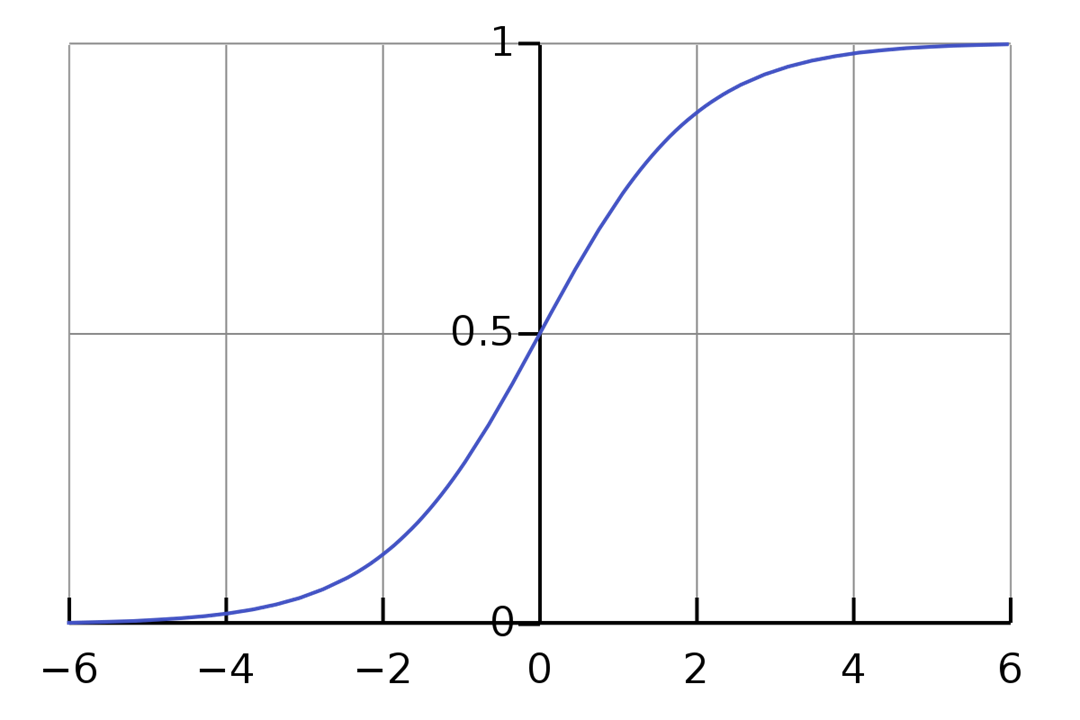
시그모이드 함수의 특성에 따라 반환값은 0 ~ 1로 고정됩니다.
이러한 점 때문에 로지스틱 회귀의 가장 큰 장점은 ⭐확률적인 접근이 가능하다⭐는 것입니다.

이제 문제는 "loss function을 어떻게 정의할 것인가?"입니다.

선형 회귀에서는 오차 "제곱"의 합을 loss로 정의했었습니다.
그런데 로지스틱 회귀의 loss function은 가중치 $w$에 대해 식 자체로도 매우 non-linear합니다. 여기에 제곱까지 해버리면 엄청나게 non-linear해져서 계산 자체가 복잡하고 오래 걸리게 될 것입니다.

그렇다고 해서 gradient descent를 쓰기에도 조금 애매합니다.

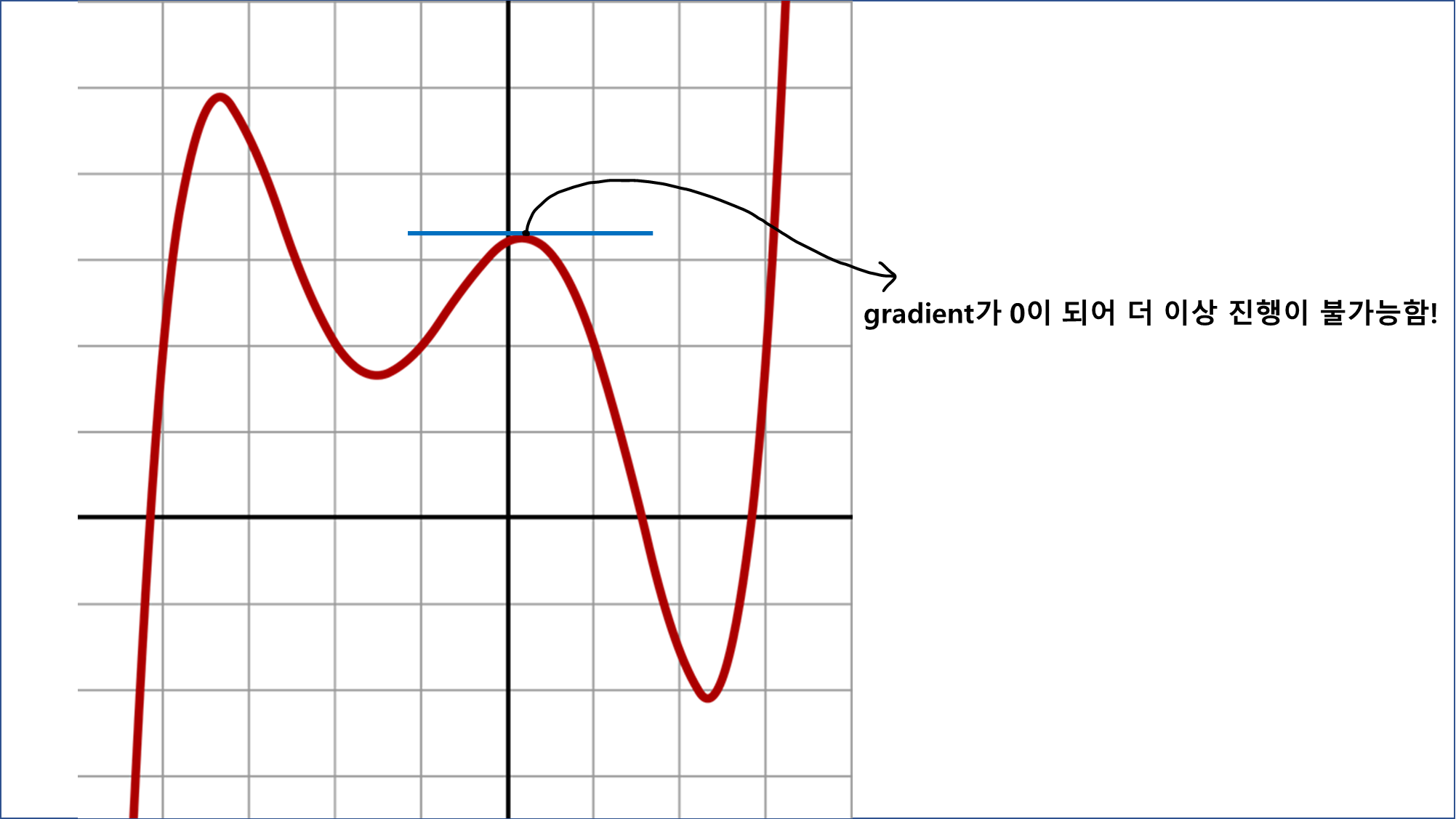
non-linear한 함수의 경우 gradient가 0이 되는 극댓값, 극솟값이 여러 군데 나타나는데, 이 때문에 값의 업데이트가 계속 진행되지 않고 중간에 멈춰버립니다.

이러한 문제 때문에 로지스틱 회귀에서는 기존 방식으로 loss function을 정의하지 않고, 가능도 (likelihood)를 기반으로 새로운 loss function을 정의합니다.

가능도 (likelihood)

---

가능도는 조건부확률과 밀접한 관계가 있습니다.

수능 문제에 많이 나오는 '주머니와 공' 문제를 예로 들어봅시다.

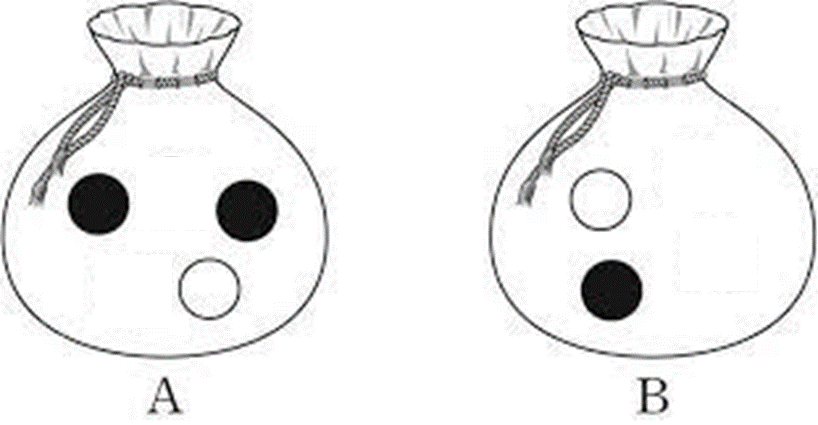
A 주머니에 검은 공 2개와 흰 공 1개가 있고, B 주머니에는 검은 공과 흰 공이 각각 1개씩 있습니다.

그러면 조건부확률은 다음과 같이 정의할 수 있습니다.

$P[검은공|A]=\frac{2}{3}$
$P[흰공|A]=\frac{1}{3}$
$P[검은공|B]=P[흰공|B]=\frac{1}{2}$

조건부확률은 조건 (A, B 주머니)을 고정하고 다른 요소를 바꾸는 것인 반면, 가능도는 원하는 요소 (검은 공 / 흰 공)를 고정하고 조건을 바꾸는 것입니다.

즉,

조건부확률 - $P[검은공|A]=\frac{2}{3}$ & $P[흰공|A]=\frac{1}{3}$
가능도 - $P[검은공|A]=\frac{2}{3}$ & $P[검은공|B]=\frac{1}{2}$

조건부확률은 모든 확률의 합이 무조건 1이지만, 가능도는 그것이 보장되지 않습니다.

5. 🐕 기계가 강아지를 학습하는 과정

---

강아지 사진을 입력으로 주고, 그 사진이 강아지 사진인지 아닌지 분류하는 문제를 가정해봅시다.
이때 입력으로 들어가는 사진은 픽셀 단위로 나눠서 벡터 형태로 표현할 수 있습니다. 간단하게 $x_1, x_2, \cdots$로 표현하겠습니다.

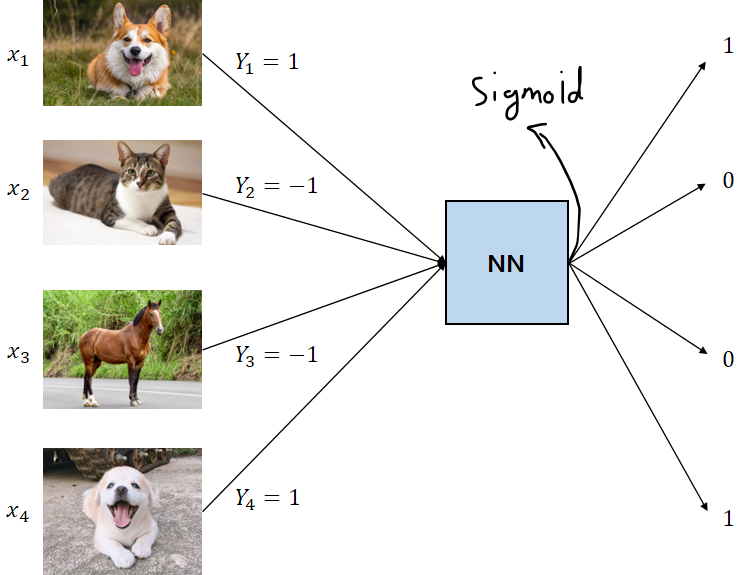
결과적으로 강아지 사진에 대한 데이터 $x_1$이 NN에 들어가고, 출력값으로 1 또는 0을 내보내야 합니다. (강아지 사진이 맞으면 1, 아니면 0)

로지스틱 회귀의 활성화 함수로 사용되는 시그모이드 함수는 0 ~ 1의 반환값을 내보내므로, 이 NN의 출력값은 입력으로 들어오는 사진이 "강아지 사진일 확률"을 의미한다고 볼 수 있습니다.

다음으로 고양이 사진 $x_2$, 말 사진 $x_3$, 강아지 사진 $x_4$가 입력으로 들어갑니다.

주의!
강아지 사진만 주구장창 준다고 해서 학습이 잘 되는 것은 아닙니다.
강아지가 아닌 사진도 입력으로 주면서 "이건 강아지가 아니야!"라고 알려주는 과정도 있어야 합니다.

이러한 과정으로 학습을 반복하다 보면 강아지 사진에 대한 output은 1에 가까워지고, 강아지가 아닌 사진에 대한 output은 0에 가까워질 것입니다.

또한, 각 데이터에는 label이 붙습니다. 강아지 사진의 label은 1, 강아지가 아닌 사진의 label은 -1. 이런 식으로요.

우리가 원하는 값은 0 또는 1이므로, 이를 위해 비용 함수 (cost function)를 수정해야 합니다.

이때 cost function은 "주어진 사진이 강아지 사진일 확률"에 대한 조건부확률로 정의할 수 있습니다.
"사진 데이터 $x_i$가 입력으로 들어왔을 때, label $Y_i$를 어떻게 정해야 하는가?"

cost function
$P[Y_i|x_i]=\begin{cases}sigmoid(f(x_i,w)) & (Y_i=1)\\1-sigmoid(f(x_i,w))&(Y_i=-1)\end{cases}$ ($w$는 입력에 관계없이 동일)

위 식에서 함수 $f$는 통과해야 할 NN이고, 이 NN을 통과한 값을 시그모이드 함수에 넣어서 확률을 구합니다.
이렇게 나온 확률 값을 최대한 크게, 정확하게 만드는 것이 목표이고, 이는 확률 값을 서로 곱함으로써 가능합니다.
(각 사건이 독립인 경우 확률의 곱셈이 가능합니다)

다음으로 loss function을 정의합니다.

앞서 정의한 cost function을 모두 곱해서 loss function을 정의할 수 있습니다.

$loss\triangleq \Pi_{i=1}^NP[Y_i|x_i]$ ($\Pi$는 수열의 모든 원소를 곱하라는 뜻)

하지만 이 값은 확률 값이기 때문에 최대한 크고 정확한 값으로 만들어야 하는데, loss function은 "줄여야 하는 값"이기 때문에 어휘상 맞지 않습니다.

따라서 앞에 -를 붙여서 $-\Pi_{i=1}^NP[Y_i|x_i]$를 loss function으로 정의합니다.

[TIP] 곱셈을 덧셈으로 바꿀 수 있는 $\log$ 함수
$\log$ 함수는 $x$가 증가하면 $y$도 증가하는 단조 함수 (monotonic function)입니다.
따라서 함수를 maximize하고자 할 때 $\log$를 씌우면 가중치에는 영향이 없습니다.
또한 $\log MN=\log M+\log N$이라는 특성에 따라 곱셈을 덧셈으로 바꿀 수 있습니다.

따라서 $Loss\triangleq-\log\Pi_{i=1}^NP[Y_i|x_i]$로 정의할 수 있으며, 최종적으로 로지스틱 회귀의 loss function은 다음과 같습니다.

$Loss\triangleq-\sum\log P[Y_i|x_i]$

6. 동물 분류 문제 (Animal Classification)

---

NN의 output node가 1개인 경우에는 앞선 분류 문제처럼 "강아지이다 / 아니다"로만 분류할 수 있고, "강아지 / 고양이 / 말"처럼 각 입력에 대해 각자의 label을 붙이는 분류는 불가능합니다.

따라서 동물 분류와 같은 다중 분류 (multi classification)에서는 출력의 종류를 동물의 종류만큼 늘리기 위해 one-hot encoding 기법을 사용합니다.

one-hot encoding은 output을 하나의 스칼라 값으로 내보내지 않고, 여러 값을 담은 벡터로 내보내는 기법입니다.

예를 들어 입력으로 들어온 사진을 강아지 / 고양이 / 소 중 하나로 분류한다고 가정하면,
$\begin{bmatrix}1\\0\\0\end{bmatrix}$는 '강아지'
$\begin{bmatrix}0\\1\\0\end{bmatrix}$는 '고양이'
$\begin{bmatrix}0\\0\\1\end{bmatrix}$는 '소'

이처럼 특정 벡터에 가까울수록 강아지, 고양이, 소 중 하나의 label로 정의할 수 있습니다.

이와 같은 다중 분류 문제에 사용되는 NN이 소프트맥스 회귀 (softmax regression)입니다.

7. 소프트맥스 회귀 (Softmax Regression)

---

소프트맥스 회귀는 소프트맥스 함수를 활성화 함수로 사용합니다.

소프트맥스 함수
$softmax=\frac{e^{x_i}}{\sum_je^{x_j}}$

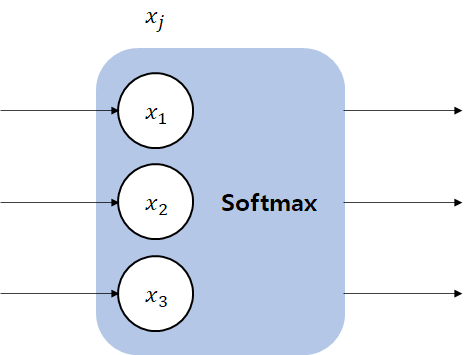
소프트맥스 함수는 시그모이드 함수의 문제점을 보완합니다.

<시그모이드 함수의 문제점>

• 값이 조금만 커지거나 작아져도 0 또는 1에 수렴한다. (saturation)
• (다중 분류의 경우) 각각의 node에 대해 상대적인 평가가 불가능하다. (두 가지 결과로 나눠지기 때문)

<소프트맥스 함수의 장점>

• saturation 문제가 발생하지 않는다.
• 각 node에 대한 상대적인 평가가 가능하다.
• $\frac{x_i}{\sum_jx_j}$처럼 단순히 normalize하는 것보다 더욱 두드러진 결과를 확인할 수 있다.

로지스틱 회귀와 비슷하게 소프트맥스 회귀 역시 확률을 기반으로 작동합니다.
로지스틱 회귀에서는 가능도 (likelihood)를 loss function으로 사용했지만, 소프트맥스 회귀에서는 Cross entropy를 loss function으로 사용합니다.

Cross entropy
$-\sum_iP_i\log q_i$ ($i$는 데이터가 아닌 벡터의 index)

$P_i$는 "원하는 확률", $q_i$는 계산해서 나온 확률 (출력값을 소프트맥스 함수에 넣어서 나온 값)입니다.

이 값을 minimize하게 되면 $q$는 $P$에 가까워지고, $q=P$일 때 값이 가장 작아집니다.

one-hot encoding은 벡터에서 하나의 element만 남깁니다. 예를 들어 벡터가 $\begin{bmatrix}1\\0\\0\end{bmatrix}$라면 다른 벡터를 곱했을 때 첫 번쨰 element만 살아남습니다.

이를 토대로 cross entropy 식을 $-\log q_k$로 줄일 수 있습니다.

다만 데이터가 여러 개일 경우, 다음과 같이 데이터의 index를 포함하여 값을 모두 더합니다.

소프트맥스 회귀의 loss function
$-\sum_i^n\log q_i$

결과적으로 로지스틱 회귀와 소프트맥스 회귀의 loss function은 동일한 형태를 가집니다. (cross entropy == likelihood)
다만 미리 계산해서 포함되는 값이 시그모이드냐, 소프트맥스냐에서 차이가 발생하는 것입니다.

• 로지스틱 회귀의 loss function - $-\sum\log P[Y_i|x_i]$
• 소프트맥스 회귀의 loss function - $-\sum_i^n\log q_i$

마무리

---

다음 포스트에서는 cross entropy를 포함한 entropy의 전반적인 내용과 함께 정보 이론을 다뤄보겠습니다.