
0. Intro
오늘은 인간의 뇌에서 영감을 얻은 학습 알고리즘인 인공 신경망 (Artifical Neural Network. ANN)에 대해 알아보겠습니다.
ANN ('A'를 빼고 'NN'이라고 부르기도 합니다)을 사용하면 선형 회귀 뿐만 아니라 비선형 회귀 (non-linear regression)까지 표현할 수 있기 때문에 많은 분야에 이용됩니다.
공부 소스 : 혁펜하임의 "꽂히는" 딥러닝 (Youtube)
1. 🧠 신경망 (Neural Network)이란?
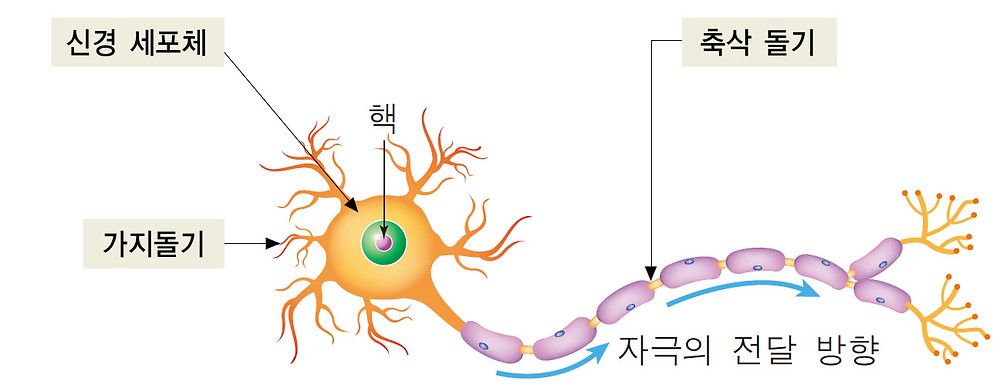 위 그림은 신경 세포의 구조입니다. (생명과학 PTSD..)
위 그림은 신경 세포의 구조입니다. (생명과학 PTSD..)
여기서 구체적인 구조는 이해하지 않으셔도 됩니다. 단지 "하나의 신경 세포에 자극이 주어지면, 신경 전달 물질을 다음 신경 세포로 넘겨준다!"라는 것만 이해하시면 충분합니다.
이렇게 생긴 신경 세포가 다발을 이룬 것을 신경망이라고 합니다.
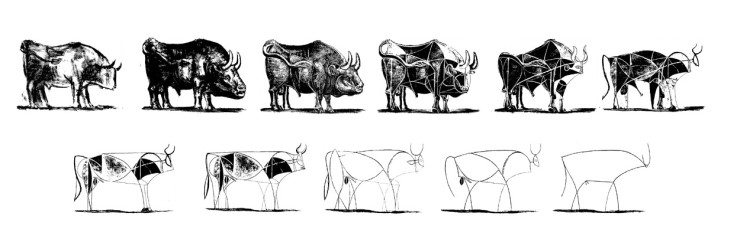 파블로 피카소의 '소'
파블로 피카소의 '소'
피카소는 소 그림을 '구체적인 형태'에서 출발하여 점점 "특징적이고 단순한 형태"로 그렸습니다.
이처럼 신경망은 무언가 특징적인 요소를 입력으로 받아서 적절한 처리를 한 뒤 다음 신경에 넘겨주게 됩니다.
2. 신경망 (NN)을 통한 선형 회귀 표현
앞선 포스트에서 정의한 것처럼 주어진 데이터셋을 가장 잘 표현하는 함수가 라고 가정해봅시다.
그러면 행렬 곱으로 다음과 같이 표현할 수 있습니다.
이때 행렬 의 값은 순차적으로 신경망 (NN)의 입력으로 들어가고, 여기에 적절한 값 를 곱하게 됩니다.
그 값이 최대한 에 가까워지도록 하는 를 찾는 것이 목표입니다.
이 구조를 그림으로 살펴볼까요?
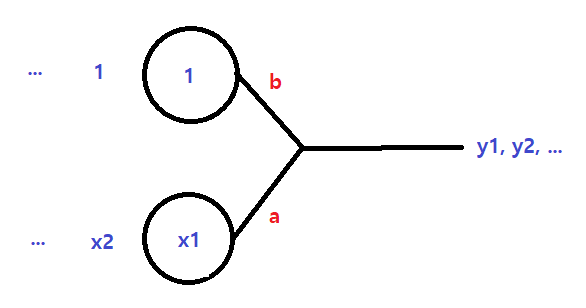
이때 와 는 이미 알고 있는 값입니다.
목표값 와 실제 데이터 간의 차이, 즉 오차를 Cost라고 하는데, cost를 최대한 줄이는 것이 핵심입니다.
신경망 중에서는 입력의 개수가 엄청나게 많은 경우도 있고, 그에 따라 찾아야 하는 와 같은 미지수가 셀 수 없이 많아질 수 있습니다.
따라서 앞으로는 기존 값에 곱해지는 값 를 가중치 (Weight)라고 칭할 것이며, 기호로 과 같이 표현하겠습니다.
또한 앞에서 말했듯이 한 신경의 결과가 다른 신경의 입력으로 들어가기 때문에 "몇 번째 신경망을 거쳐가는지"에 대한 layer가 존재합니다.
몇 번째 layer의 가중치인지 표현하기 위해 와 같이 표기하겠습니다.
- 1번 layer의 2번 가중치
- 2번 layer의 3번 가중치
📒 여러 가지 선형회귀 식
NN을 통해 다양한 선형 회귀를 표현할 수 있습니다.
는 아까 했으니 넘어가고, 4개의 식을 NN으로 표현해보겠습니다.
와 행렬 구성만 다를 뿐, 표현하는 방식은 비슷합니다.
이 식을 행렬 곱으로 표현하면 다음과 같습니다.
따라서 다음과 같이 NN으로 표현이 가능합니다.
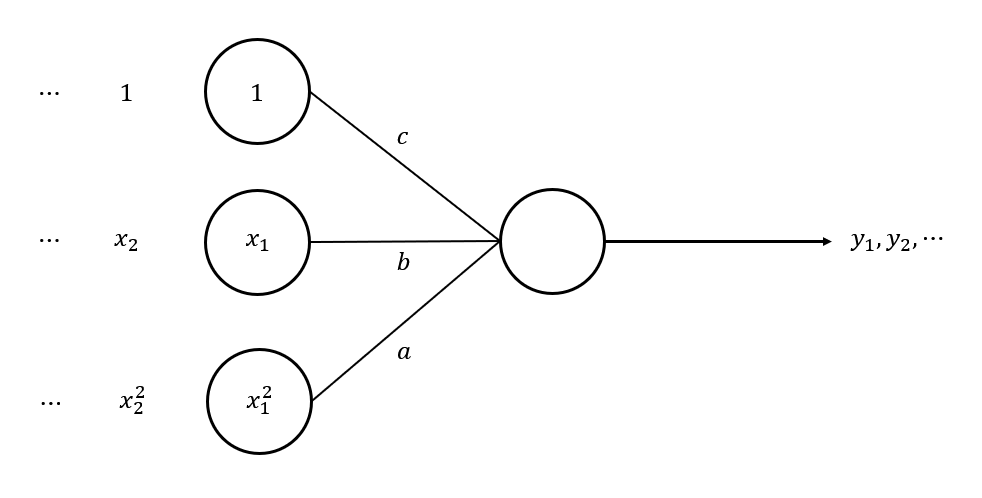
❗ 주의할 점
꼭 함수가 linear해야만 linear regression이 성립되는 것은 아닙니다. 가 아닌, 파라미터 에 대해 linear해야 linear regression이 성립하는 것입니다.
('행렬 x 벡터' 형태로 표현할 수 있는 것은 모두 linear합니다)
의 경우, 에 대해서는 non-linear한 식이지만 에 대해서는 linear한 식입니다.
이 함수는 앞의 다른 함수와는 다르게 접근해야 합니다.
먼저 양변에 자연로그 을 취하면
이때 를 (tilde y)로, 를 로, 를 로 치환해봅시다.
어디서 많이 보지 않았나요?
처음에 다뤘던 와 동일한 형태가 되었습니다!
다시 이를 행렬 곱으로 표현하면,
즉, 파라미터 에 대해 linear한 상태가 되었습니다.
이처럼 "원 형태 그대로는 linear하지 않지만, 어떠한 조치를 취하면 linear한 상태가 되는 함수"를 ⭐선형화 가능한 (linearizable)⭐ 함수라고 합니다.
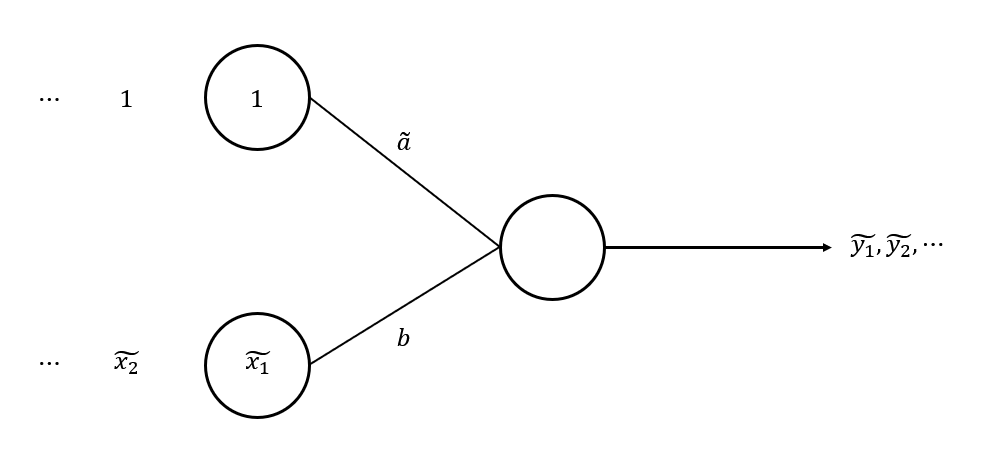
이 함수 역시 linearizable한 함수입니다.
로 함수의 형태를 바꿔봅시다.
이때 양변에 자연로그 을 취하면
여기서 를 로 치환하면 와 동일한 형태가 되고, linear한 함수가 됩니다.
행렬 곱으로 표현하면
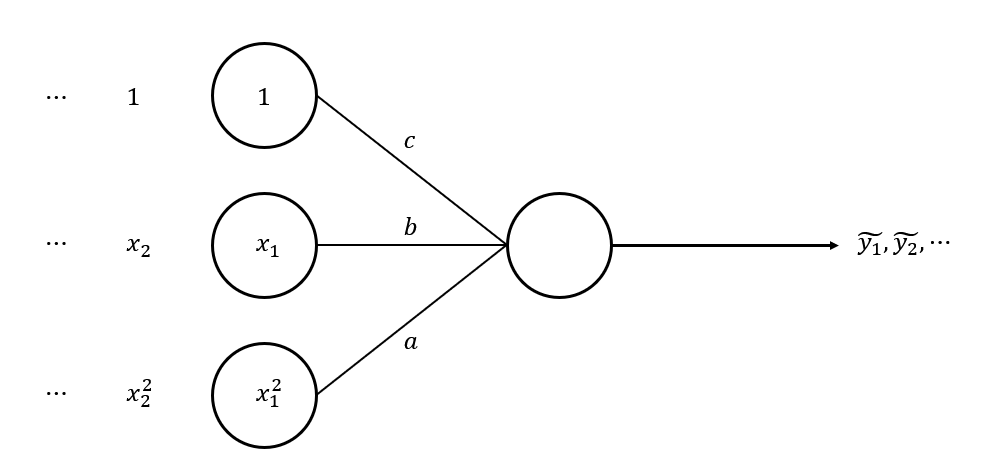
이 함수는 어떤 짓을 해도 linear한 함수로 만들 수 없습니다.
따라서 non-linear regression에 해당합니다.
3. "Deep" Neural Network (DNN)
과 같은 non-linear regression을 해결하기 위해 뉴런 (신경망의 개별 요소)을 여러 개 연결하여 말 그대로 신경망 자체를 "deep"하게 만드는 것이 가능합니다.
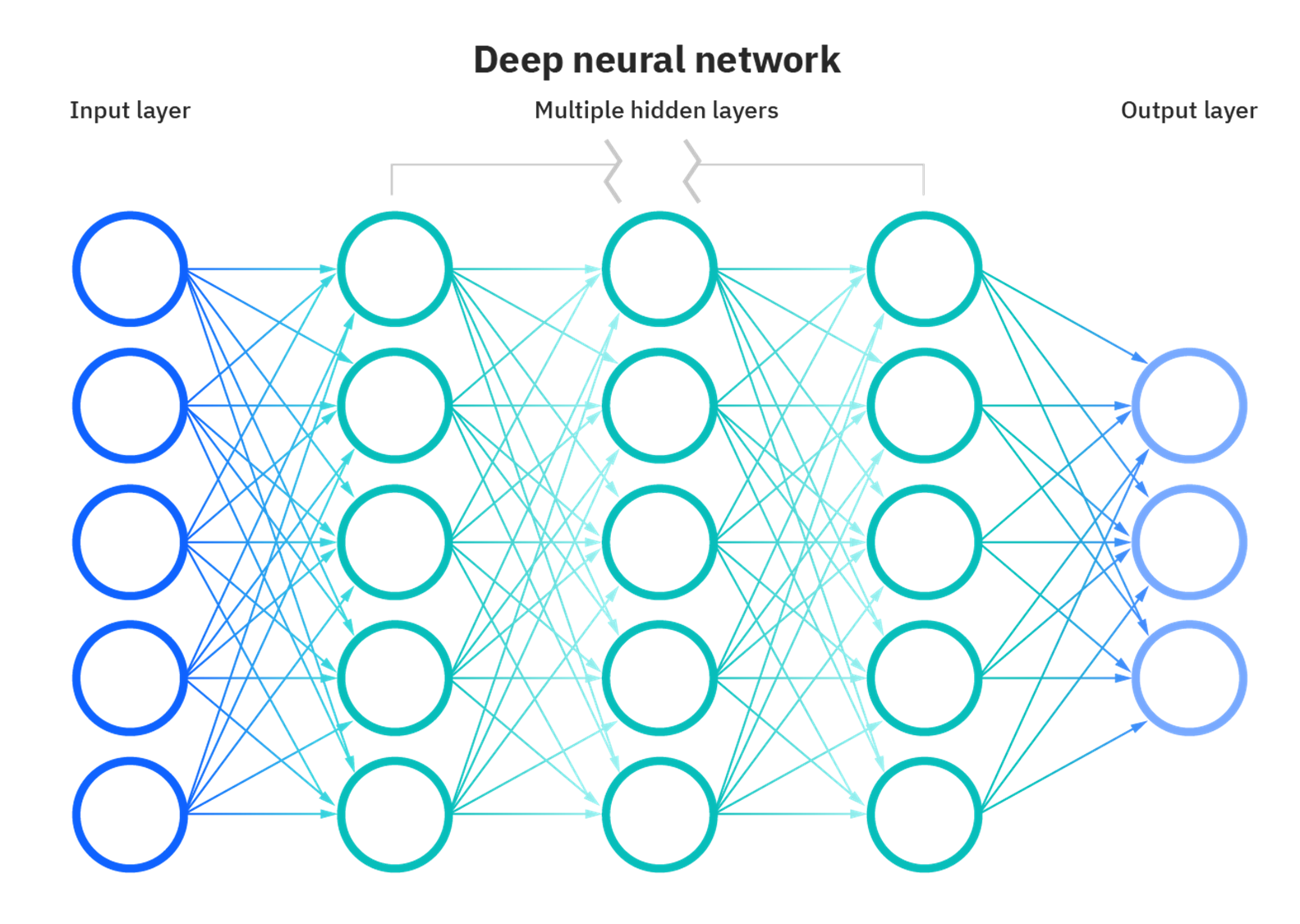 출처 : IBM
출처 : IBM
즉, 하나의 뉴런에서 입력을 처리한 뒤 바로 출력으로 내보내지 않고, 다른 뉴런의 입력으로 사용하는 것을 말합니다.
하지만 무조건 "Deep"하다고만 해서 non-linear regression을 풀 수 있는 것은 아닙니다.
예를 들어 다음과 같은 신경망이 있다고 가정해보죠.
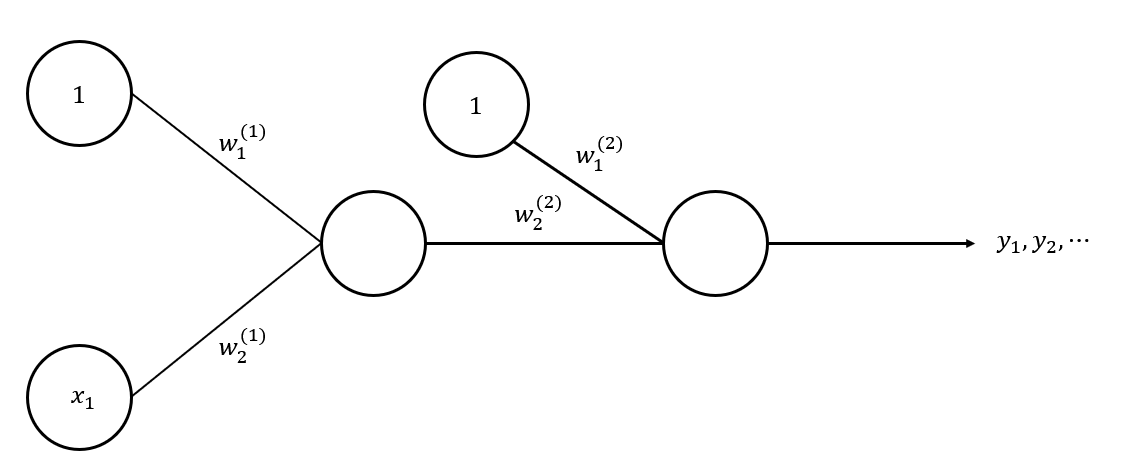
이 신경망을 하나의 식으로 작성하면 다음과 같이 표현할 수 있습니다.
이를 다시 쓰면
이 식은 인 함수와 동일한 형태가 됩니다.
따라서 이 함수 역시 linear regression이 되는 것입니다.
4. 💥 활성화 함수
지금까지는 한 뉴런에서 다른 뉴런으로 값을 보낼 때 아무런 처리도 하지 않고 그대로 보냈습니다.
하지만 실제로는 특별한 처리를 한 뒤에 다른 뉴런으로 보냅니다.
이 "특별한 처리"는 활성화 함수 (Activation Function)를 통해 이루어지는데, 지금까지는 이 활성화 함수가 였기 때문에 입력값이 그대로 출력값으로 전달되는 것이었고, 이제부터는 활성화 함수를 새롭게 정의하여 출력값에 변화를 줄 것입니다.
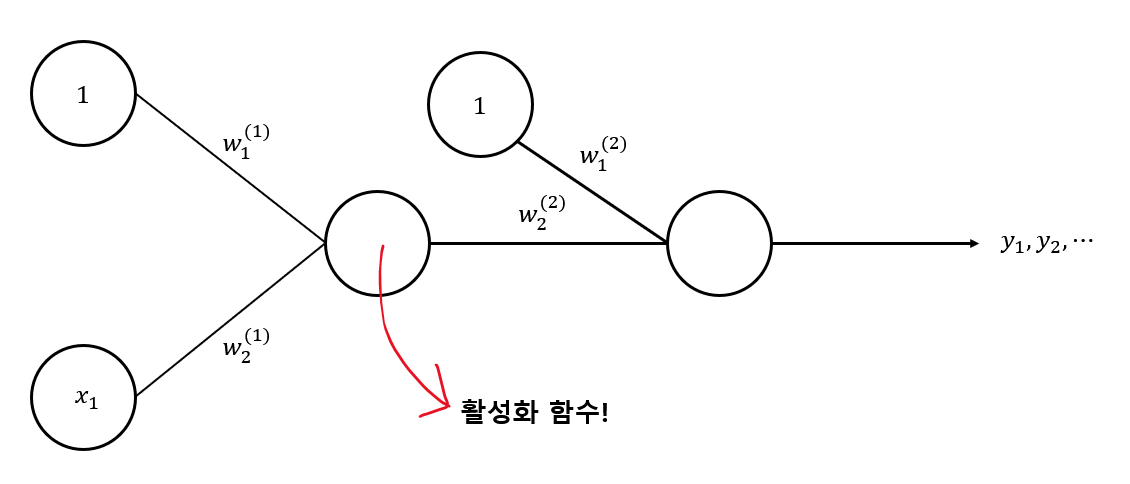
활성화 함수에 따른 NN 분류
활성화 함수가 non-linear 함수라면 non-linear regression을 표현할 수 있습니다.
-
하나의 layer를 갖는 NN에서 활성화 함수가 인 경우
→ linear regression -
활성화 함수가 계단 함수 (step function)인 경우
→ 퍼셉트론 (Perceptron)
계단 함수
구간에 따라 상수를 반환하는 함수
계단 함수의 종류에는 step, sign 함수 등이 있다.
step function
sign function
- 활성화 함수가 시그모이드 함수 (sigmoid function)인 경우
→ 로지스틱 회귀 (Logistic Regression)
시그모이드 함수
값이 커질수록 1에 수렴하고, 작아질수록 0에 수렴하는 함수 (중간값은 0.5)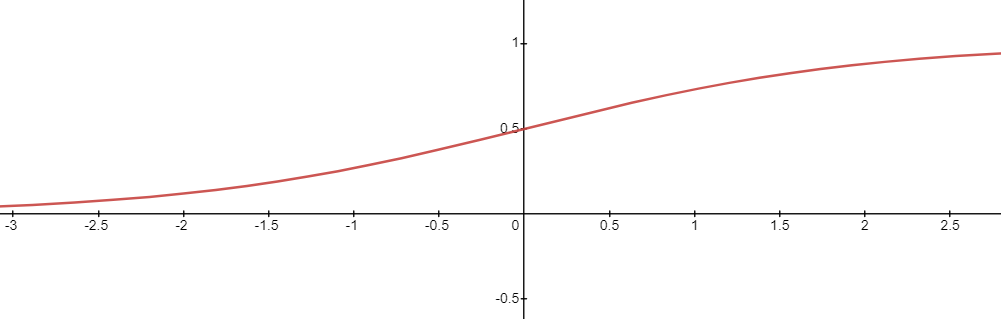
- (출력 node가 여러개일 때) 활성화 함수가 인 경우
→ 소프트맥스 회귀 (Softmax Regression)
퍼셉트론과 로지스틱 회귀, 소프트맥스 회귀에 대해서는 다음 포스트에서 조금 더 자세히 다루도록 하겠습니다 :)
