0. Intro

---

이전 포스트에서 이야기했던 것처럼 결국 $(y-Ax)^T(y-Ax)$를 최소화하는 $x$를 찾는 것이 선형 회귀의 핵심이고, $x$에는 찾고자 하는 파라미터 $a,b$가 포함되어 있습니다.

기존 데이터를 통해 충분히 학습시킨 machine은 최종적으로 함수 $y=ax+b$를 도출할 것이고, 테스트 (test)를 통해 새로운 데이터, machine이 모르는 데이터를 함수에 대입하여 올바른 값이 나오는지 확인할 수 있습니다.

오늘은 에러를 줄이기 위해 $x$를 업데이트하는 방법 중 대표적인 경사하강법 (Gradient Descent)과 Newton Method에 대해 알아보려고 합니다.

공부 소스 : 혁펜하임의 "꽂히는" 딥러닝 (Youtube)

1. Gradient Descent (경사하강법)

---

앞서 정의했던 $y-Ax$가 1차 함수 형태이기 때문에 이를 제곱한 $||(y-Ax)||^2=(y-Ax)^T(y-Ax)$는 2차 함수 형태입니다.

경사하강법에서는 초기값은 임의로 지정하고, 목표값과의 오차를 줄여가면서 최대한 목표값에 가깝도록 만듭니다.

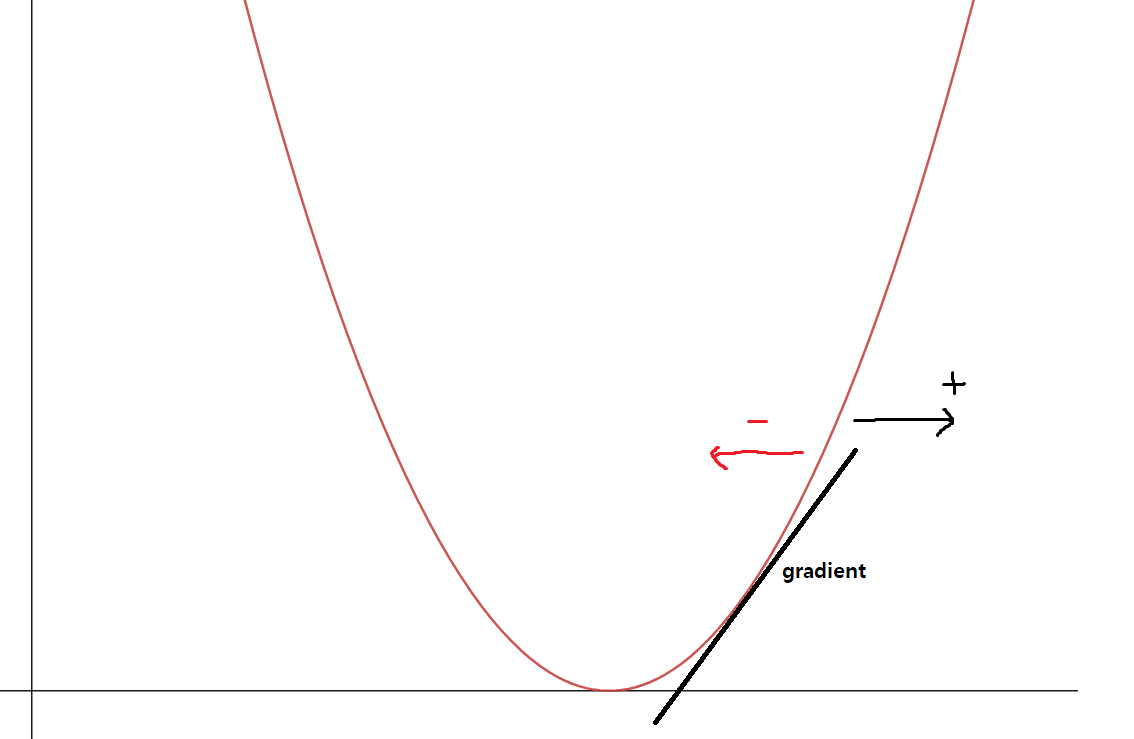
여기서 Gradient를 이용하는데, gradient는 함수가 가장 빠르게 증가하는 방향을 알려줍니다.
따라서 gradient를 통해 얻은 방향과 반대되는 방향으로 값을 업데이트하다보면 오차가 줄어들게 될 것입니다.

예를 들어 $(x-3)^2$을 미분하면 $2(x-3)$이 되는데, 이 값은 3을 기준으로 양수, 음수가 나뉩니다.
음수일 경우 왼쪽으로 가파른 방향이고, 양수일 경우 오른쪽으로 가파른 방향을 나타냅니다.

즉, 초기값에서 출발하여 미분한 값이 0에 가까워지는 방향으로 값을 업데이트하는 것이 경사하강법이라고 할 수 있습니다.

결국 $||(y-Ax)||^2=(y-Ax)^T(y-Ax)$를 미분한 뒤 그 값을 통해 업데이트를 진행해야 합니다.

다만 여기서 $x$는 $x=\begin{bmatrix}a\\b\end{bmatrix}$와 같은 벡터 형태이고, $a,b$라는 두 개의 파라미터가 존재합니다. 따라서 $a$에 대해서 미분해야 하고, $b$에 대해서도 미분을 해야 합니다. (편미분)

즉 $f(a,b)$라는 함수가 있을 때 $\operatorname{d}\!f=\frac{\partial f}{\partial a}\operatorname{d}\!a+\frac{\partial f}{\partial b}\operatorname{d}\!b$처럼 나타낼 수 있습니다.

이 식을 행렬 곱의 형태로 표현하면

$\begin{bmatrix}\frac{\partial f}{\partial a} & \frac{\partial f}{\partial b}\end{bmatrix}\begin{bmatrix}\operatorname{d}\!a\\\operatorname{d}\!b\end{bmatrix}$

여기서 gradient는 $\begin{bmatrix}\frac{\partial f}{\partial a} & \frac{\partial f}{\partial b}\end{bmatrix}$입니다.

그런데 $x\triangleq\begin{bmatrix}a\\b\end{bmatrix}$라고 정의했으므로 gradient를 $x$를 통해 표현하면 다음과 같습니다.

⭐ $\frac{\partial f}{\partial x^T}\operatorname{d}\!x$ ⭐

앞서 말했듯 gradient는 "함수가 가장 빠르게 증가하는 방향"을 알려주기 때문에, 경사하강법에서는 반대 방향으로 진행하며 값을 업데이트합니다.
결국 경사하강법의 핵심은 gradient를 구하는 것입니다.

📕 TIP!

---

$a,b$에 대한 편미분을 따로 구하지 않고 한번에 gradient를 구하는 방법이 있습니다.

$\operatorname{d}\!f$를 구하면 최종적으로 $\frac{\partial f}{\partial x^T}\operatorname{d}\!x$가 나오는데, 여기서 $\operatorname{d}\!x$를 제외한 앞 식이 gradient입니다.

그런데 $\operatorname{d}\!f$는 어떻게 구할까요?

이론적으로는 $\operatorname{d}\!f=\lim_{\operatorname{d}\!x\rightarrow 0}\frac{f(x+\operatorname{d}\!x)-f(x)}{\operatorname{d}\!x}$입니다.
여기서 $\operatorname{d}\!x^2$과 같은 2차항은 분모에 있는 $\operatorname{d}\!x$로 나눠지므로 의미가 없습니다. 따라서 1차항만 고려하여 미분 식을 전개합니다.

$f(x)=(y-Ax)^T(y-Ax)$라고 가정하면, ($F.O.$ = 1차항만 고려하겠다는 뜻)

$F.O.[f(x+dx)-f(x)]\\=(y-A(x+dx))^T(y-A(x+dx))-(y-Ax)^T(y-Ax)\\=((y-Ax)-Adx)^T((y-Ax)-Adx)-(y-Ax)^T(y-Ax)\\=-dx^TA^T(y-Ax)-(y-Ax)^TAdx$

이전 포스트에서 정의했듯 행렬 $A$는 $n\times 2$ 행렬이고, $x$는 $2\times 1$ 행렬입니다. 따라서 이 둘을 곱한 $Ax$는 $n\times 1$ 행렬이 되므로 이는 스칼라 (Scalar) 형태가 됩니다.

스칼라에서는 $a^Tb=b^Ta$가 성립합니다. 따라서 기존 행렬과 transpose를 취한 행렬이 서로 동일합니다.

이에 따라 $dx^TA^T(y-Ax)=(y-Ax)^TAdx$이고, 따라서

⭐ $df=-2(y-Ax)^Adx$ ⭐

$dx$ 앞에 있는 term은 모두 gradient에 해당하므로 gradient는 $-2(y-Ax)^TA$입니다.
따라서 $x$ 값은 gradient의 방향인 $-2(y-Ax)^TA$의 반대 방향으로 업데이트되어야 오차를 줄이면서 목표 값에 가까워질 수 있습니다.

$x_{i+1}=x_i+2A^T(y-Ax_i)$ (gradient는 $1\times 2$ 행렬이므로 transpose)

하지만, gradient는 방향에 대한 정보만 전달하기 때문에 기존 값을 얼만큼 업데이트해야 적절한 속도로 목표 값에 도달하는지는 데이터와 함수에 따라 천차만별입니다.
따라서 Learning Rate라는 적절한 값을 곱한 뒤 더해주어야 합니다.

learning rate가 너무 크면 값의 변화가 큼직하기 때문에 정확한 값에 도달하기 힘들고, 반대로 너무 작으면 학습 속도가 느려지므로 적절한 learning rate를 선택하는 것이 중요합니다.

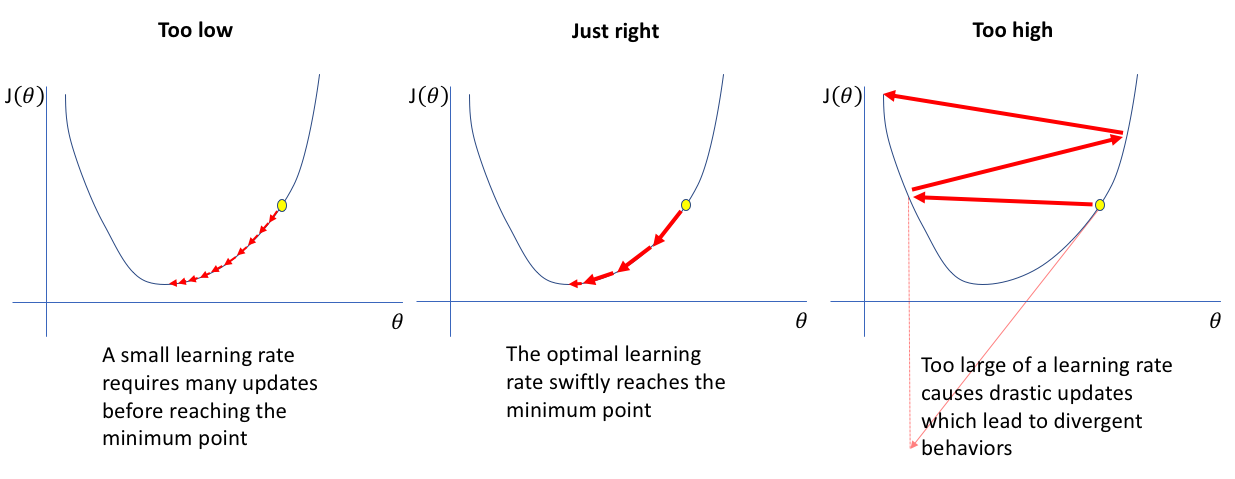출처 : Jeremy Jordan

2. Newton Method (뉴턴 방법)

---

newton method는 learning rate의 값을 정확히 제시한 방법입니다.
하지만 2차 미분을 사용하기 때문에 실제로 많이 사용하지는 않는 방법입니다.

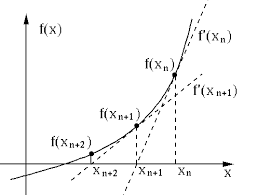
위 그림처럼 초기값에서의 접선이 $x$축과 닿는 지점으로 $x$를 업데이트하고, 그 지점에서 다시 접선을 구한 뒤 이를 반복합니다.

newton method는 기본적으로 zero-finding입니다.
업데이트 식은 다음과 같습니다.

$x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)}$

이때 $f'(x_k)$는 아까 gradient descent에서 구한 식 $-2(y-Ax)^TA$와 같습니다. 따라서 learning rate는 $\frac{1}{f''(x_k)}$입니다.

newton method를 사용하면 one step 만에 가까운 해답을 찾을 수 있습니다. 하지만 계산 과정이 복잡하고 오래 걸리기 때문에 잘 쓰지 않는 방법입니다.

newton method의 단점을 개선하고 발전시킨 방법이 Quasi-Newton Method입니다. 2차 미분을 근사 (approximate)하는 방법입니다.

마무리

---

이 포스트에 나온 gradient, newton method와 같은 내용은 제가 정리한 다른 포스트에서 자세히 확인하실 수 있습니다.