0. Intro

방학 때 진행할 프로젝트에서 딥러닝을 사용할 기회가 생겼는데, 딥러닝을 1도 모르는 까막눈 상태라 프로젝트 시작 전에 빠르게 딥러닝 기초를 공부할 생각으로 포스팅을 기획했습니다.

공부 소스 : 혁펜하임의 "꽂히는" 딥러닝 (Youtube)
참고 : 혼자 공부하는 머신러닝+딥러닝

지인의 추천을 받고 영상을 찍먹해 봤는데 개념 정리도 깔끔하고 좋았습니다. 그래서 이 영상을 보고, 제 나름대로 정리 + 추가적인 개념을 더해서 포스팅하도록 하겠습니다 ^_^

---

1. 머신러닝? 강화학습?

[출처: Atria Innovation]

딥러닝을 공부하기 전에 머신러닝 (Machine Learning)과 강화학습 (Reinforcement Learning)이 무엇인지 알 필요가 있습니다.

머신러닝 (Machine Learning)
: 데이터 (data)를 활용하여 여러 작업의 성능을 향상시키는 방법 (method)을 학습 (learning)하기 위한 방법을 이해하고 구축하는 탐구 분야 [출처: wikipedia]

뭔가 장황하고 복잡하게 설명되어있는데, 쉽게 생각하면 말 그대로 기계 (machine)가 무언가를 학습 (learning)하는 것입니다.

간단한 예를 들어보겠습니다.

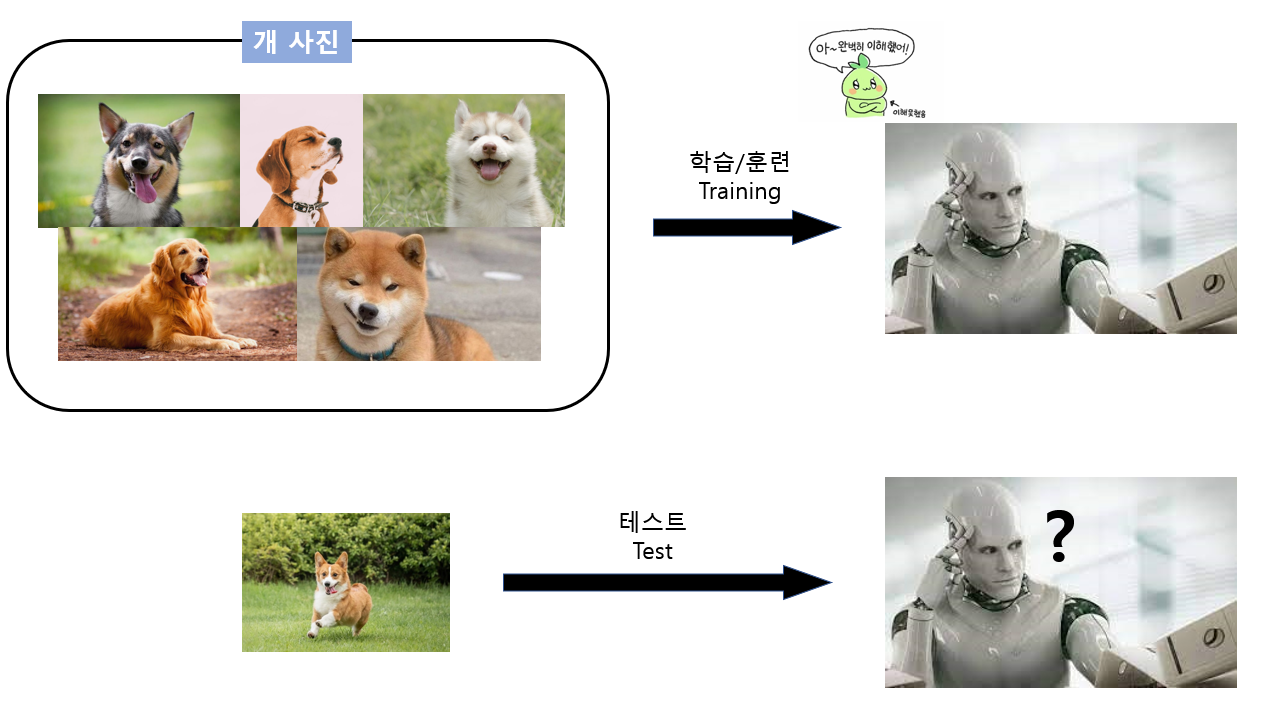
기계에게 여러 장의 개 사진을 보여준 다음, 새로운 개 사진을 보여주면 이 기계는 사진 속 동물이 '개'라는 것을 알 수 있을까요?

이때 기계에게 여러 장의 개 사진을 보여주는 과정을 학습/훈련 (Training)이라고 하고, 새로운 개 사진을 보여주면서 기계가 잘 인식하는지 확인하는 과정을 테스트 (Test)라고 합니다.

즉, 학습을 통해 기계를 훈련시키고, 학습이 잘 되었는지 확인하기 위해 테스트를 진행하는 것이라고 할 수 있겠습니다.

그런데, 이 학습 과정에는 특징이 있습니다.
학습에 쓰이는 사진들이 '개'를 나타내는 사진이라고 알려주면서 학습을 진행하는데, 이처럼 훈련에 쓰이는 데이터에 대해 "미리 정답을 알려주고 학습시키는" 것을 지도 학습 (Supervised Learning)이라고 합니다.

반대로 비지도 학습 (Unsupervised Learning)은 훈련 데이터에 대해 정답을 알려주지 않고, 기계 스스로 데이터 간의 관계를 파악하여 일종의 패턴을 유추해나가는 학습 방법입니다.

머신러닝에는 또다른 종류의 학습 방법이 존재하는데, 그것은 바로 강화학습 (Reinforcement Learning)입니다.
강화학습은 비지도 학습과 비슷하지만 약간 다른데, 현재 상태 (state)에서 어떤 행동을 했을 때 보상을 최대화하는 방향으로 학습하고 행동해나가는 방식입니다.
(강화학습에 대해서는 추후 자세히 다뤄보겠습니다 ^^)

요약하자면, 기계를 학습시켜서 인간이 직접 프로그래밍하지 않더라도 기계가 스스로 학습한 데이터를 토대로 규칙을 파악하도록 하는 것이 머신러닝이고, 머신러닝의 학습 방법에는 지도 학습, 비지도 학습, 강화학습이 있습니다.

---

2. 선형 회귀 (Linear Regression)

종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법 [출처 : wikipedia]

이번에도 뭔가 복잡한 설명이 나왔네요. 수포자인 저로써는 막막하기만 합니다 ㅠ.ㅠ
그래도 최대한 간단하게 설명해보겠습니다!

선형 회귀는 함수를 근사 (approximate)하는 방법 중 하나입니다.

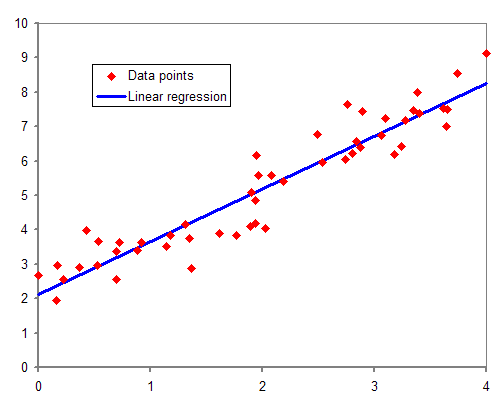[출처: wikipedia]

여기서 빨간 점은 실제 데이터들이고, 이 데이터들 간의 상관관계를 가장 잘 표현하는 하나의 linear한 함수 (보통 직선을 의미합니다)를 찾는 것이 선형 회귀입니다.

[출처: wikipedia]

이를 위해서는 실제로 주어진 데이터 (관측값, 위 그림에서 빨간 점)와 예측값 (파란 직선) 사이의 오차 (error)를 최소화하는 방향으로 함수를 찾아야 합니다.

간단한 수식을 통해 자세히 알아봅시다.

관측값 $x_1,x_2,x_3,\cdots$와 예측값 $y_1,y_2,y_3,\cdots$가 있다고 가정합니다.
이 데이터들을 표현하는 함수의 형태가 $y=ax+b$라고 하면, 데이터 간의 관계를 가장 잘 표현해주는 $a,b$를 찾는 것이 선형 회귀라고 할 수 있습니다.

관측값과 예측값을 식에 대입해보겠습니다.
$y_1\approxeq ax_1+b\\y_2\approxeq ax_2+b\\y_3\approxeq ax_3+b\\\vdots$
($\approxeq$ : 근사치)

즉, 관측값을 식에 넣었을 때 최대한 예측값에 가까워지도록 하는 $a,b$를 찾아야 합니다.

지금 이 식의 경우 여러 개의 식이 나열된 형태입니다. 이 형태는 해를 찾는 것이 복잡하니 간단하게 행렬 (matrix) 형태로 바꿉니다.

$\begin{bmatrix}x_1 & 1\\x_2 & 1\\\vdots\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}y_1\\y_2\\\vdots\end{bmatrix}$
(행렬을 실제로 곱해보면 위 식과 동일한 형태가 나올 것입니다)

여기서 더 단순화하기 위해 행렬과 벡터의 곱으로 표현할 수 있습니다. (이때 말하는 벡터는 단순히 '수의 모음'입니다)

$A\vec{x}\approxeq\vec{y}$

이렇게 해서 관측값과 예측값의 관계를 간단한 식으로 나타냈습니다.
$A\vec{x}$가 관측값이고, $\vec{y}$가 예측값이기 떄문에 오차는 $\vec{y}-A\vec{x}$로 표현할 수 있습니다.

이제 생각해야 할 것은 "이 오차를 어떻게 다룰지"에 대한 것입니다.

1. 절댓값 [출처: wikipedia]

이 그림을 다시 한번 봅시다.
$\vec{y}-A\vec{x} > 0$인 경우 예측값이 관측값보다 크기 때문에 오차가 양수이고, $\vec{y}-A\vec{x} < 0$인 경우 예측값이 관측값보다 작기 때문에 오차가 음수가 됩니다.

대부분의 알고리즘에서는 이 오차를 더한 값을 최소화합니다. 이때 $-2+2=0$과 같이 실제로 오차가 있지만 더해졌을 때 상쇄되는 일이 없어야 하기에, 오차에 절댓값을 취하는 방식을 사용합니다.

2. 절댓값의 제곱
   

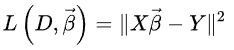
선형 회귀에서는 절댓값의 제곱으로 오차를 계산하는 방식을 많이 사용합니다.
절댓값만으로 오차를 계산하지 않는 이유는 "unbiased estimator를 구하기 쉬운 것이 절댓값의 제곱이기 때문"인데, 이는 표준편차가 편차의 제곱의 평균인 이유와 비슷합니다. (자세한 내용은 시간이 되면 추가 포스팅하겠습니다)

그런데 여기서 또다른 문제가 발생합니다.
Gradient Descent와 같은 방식에서는 이 오차를 미분하는데, 절댓값을 갖는 함수는 미분 시 구간을 나눠서 미분해줘야 하기 때문에 다소 복잡합니다.

앞서 말했듯 $\vec{y}-A\vec{x}$는 행렬로 표현한 형태이기 때문에, 행렬의 특징을 이용하여 이 문제를 해결할 수 있습니다.

대칭행렬 $A$에 대해 $A^TA=A^2$

즉, 행렬을 transpose한 것과 원래 행렬을 곱하면, 그 행렬의 제곱이 됩니다. (대칭행렬에 한함)

따라서 구간을 나눠서 미분하지 않고 행렬을 통해 오차의 제곱을 구할 수 있습니다.
$(\vec{y}-A\vec{x})^T(\vec{y}-A\vec{x})=|(\vec{y}-A\vec{x})|^2$

선형 회귀의 핵심인 "오차 최소화"는 크게 3가지 방법이 있는데, 이는 다음 포스팅에서 자세히 설명합니다.

1. Gradient Descent
2. Newton-Rapshon method
3. Least square - 위 방식과는 달리 iteration을 돌지 않고, 식 계산 한번으로 solution을 빠르게 구할 수 있다는 것이 장점입니다.