기본 개념 익히기 - AI, ML, DL
-
인공지능 : 기계가 사람의 행동을 모방하게 하는 기술
-
기계학습 : 기계가 일일이 코드로 명시하지 않은 동작을 데이터로부터 학습하여 실행할 수 있도록 하는 알고리즘을 개발하는 연구 분야
-
기계 학습의 한 분야인 인공 신경망에 기반하여, 많은 양의 데이터를 학습해 뛰어난 성능을 이끌어내는 연구 분야
-
빅데이터 : 딥러닝 연구에서 다루지 않는 부분
- 데이터베이스 관리
- 데이터 저장/유통
- 데이터 수집
- 데이터 신뢰성 확보
- 데이터 시각화
- 데이터 통계 분석
- 데이터 마이닝 -
딥러닝 구성요소 :
- 학습 데이터 셋 → 학습 입력 → 네트워크 구조 → 손실함수 → 알고리즘 최적화 기법
- 학습단계 : 테스트 입력 → 학습된 네트워크 → 평가지표
- 뉴런의 그래프 표현 : 보통 신경망을 표현할 때, Graph의 Node와 Edge를 이용해 표현한다. 여기서 Node는 단일 뉴런 연산을, Edge는 뉴련의 연결성을 의미
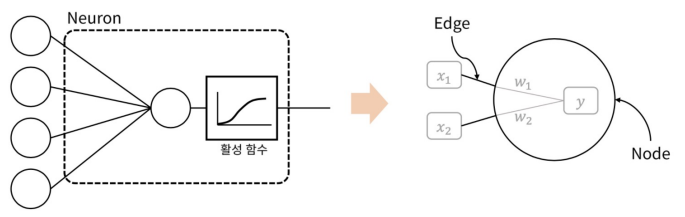
-
Fully-connected layer : 뉴런이 모인 한 단위를 계층(Layer)라고 하며, 이전 계층과 모든 뉴런이 서로 연결된 계층을 Fully-Connected Layer(Dense Layer)라고 한다
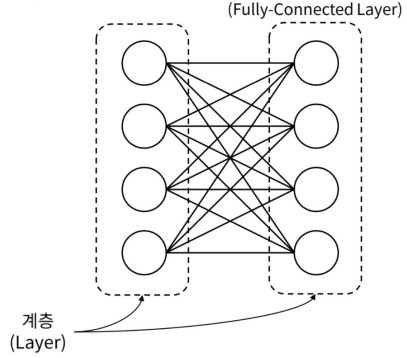
-
얇은 신경망 : 입력, 은닉, 출력의 3가지 계층으로 되어 있으며, 은닉 계층과 출력 계층이 Fully Connected 계층인 모델을 얇은 신경망(Shallow Neural Network)라고 한다
-
얇은 신경망으로 할 수 있는 것 :
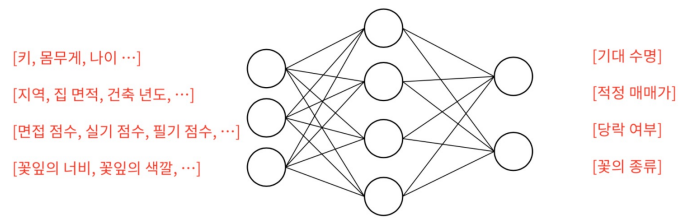
-
회귀 : 잡음이 있는 학습 샘플로부터 규칙을 찾아 연속된 값의 출력을 추정하는 것.
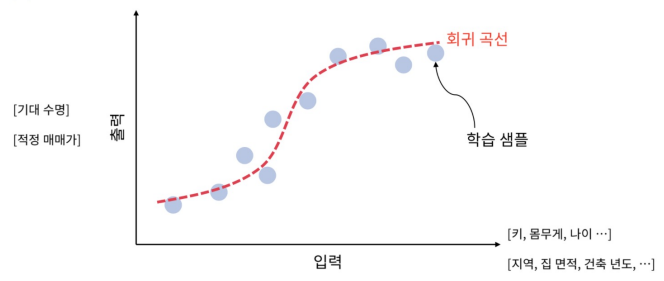
-
얇은 신경망을 이용한 회귀 : 얕은 신경망의 동작은 출력 계층의 활성 함수에 의해 달라진다. 회귀는 전 범위의 연속된 값을 출력하므로, 보통 Identity function(항등 함수)을 사용
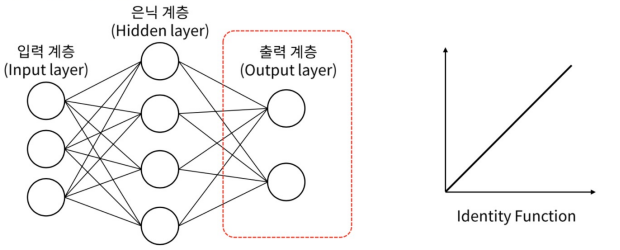
-
분류 : 입력 값을 분석해 특정 범주(Category)로 구분하는 작업. 범주가 2개일 경우 '이진 분류(Binary classification)', 그 이상은 '다중 분류(Multi-class classification)'라고 한다.
-
얇은 신경망을 이용한 이진 분류 : 이진 분류를 위한 출력은 0 - 1 사이의 실수 값이며, 활성함수로 sigmoid function을 사용. 0.5보다 작으면 첫 번째 class, 0.5보다 크면 두 번째 class로 분류
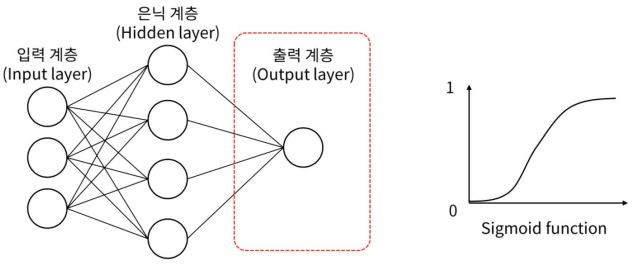
-
다중 분류 : SoftMax 활성 함수를 이용해 다중 분류 문제를 해결 가능. 각 출력은 해당 class에 속할 확률을 의미
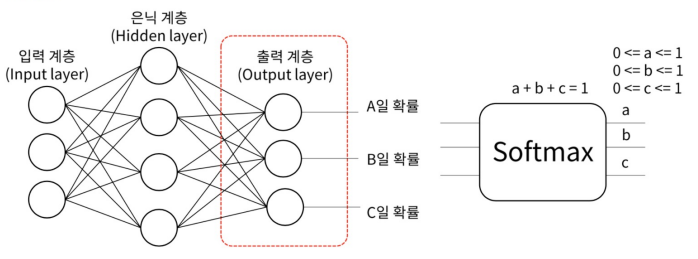
-
뉴런은 수학적으로 두 벡터의 내적으로 쉽게 표현 가능
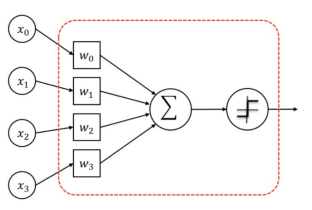
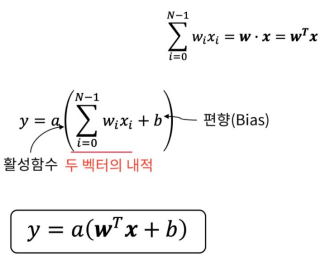
-
Fully-connected layer의 수학적 표현 : FC 계층은 여러 개의 뉴런을 한 곳에 모아둔 것으로 Matrix 곱셈 연산으로 표현된다

-
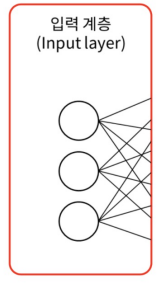
Input Layer : 입력계층.
- 입력계층은 아무런 연산도 일어나지 않는다
- 신경망의 입력을 받아서 다음 계층으로 넘기는 역할
- 무엇을 입력으로 주어야 하는가? → 특징 추출 문제
- 계층의 크기 = Node의 개수 = 입력 Scalar의 수 = 입력 Vector의 길이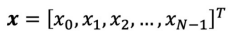
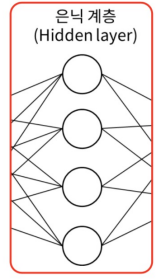
- Hidden Layer : 은닉계층
- 은닉 계층은 입력 계층과 연결된 전결합 계층이다
- 입출력 관점에서 볼 때 드러나지 않는다고 하여, 은닉 계층이라 한다
- 복잡한 문제를 해결할 수 있게 하는 핵심적인 계층
- 얕은 신경망에서는 1개의 은닉 계층만을 사용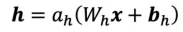
- Output Layer : 출력계층
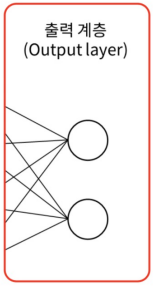
- 출력 계층은 은닉 계층 다음에 오는 전결합 계층이다
- 신경망의 외부로 출력 신호를 전달하는 데에 사용된다
- 신경망의 기능은 출력 계층의 활성 함수에 의해 결정된다
- 출력 계층의 크기 = 출력의 Scalar 수 = 출력 벡터의 길이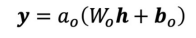
-
회귀 : 연속된 값을 추정하는 회귀(Regression)
-
선형회귀 (Linear Regression) : 데이터를 가장 잘 표현하는 선형식을 찾는 동작. 단순 선형 회귀의 예) 독립 변수(입력)이 하나이므로, 추정해야 할 변수도 하나. 단, 편향을 포함하면 2개가 된다

-
다중선형회귀 :
- 단일 입력이 아닌, 다중 입력을 받을 경우에는 변수가 확정되어 벡터의 내적이 된다
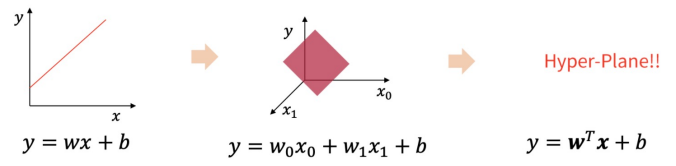
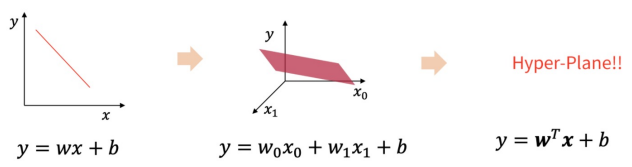
- 변수가 하나 추가될 때마다 차원이 하나씩 추가된다. 직선 → 평면 → 초평면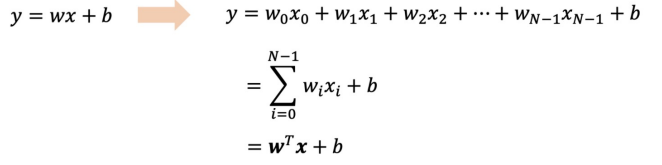
-
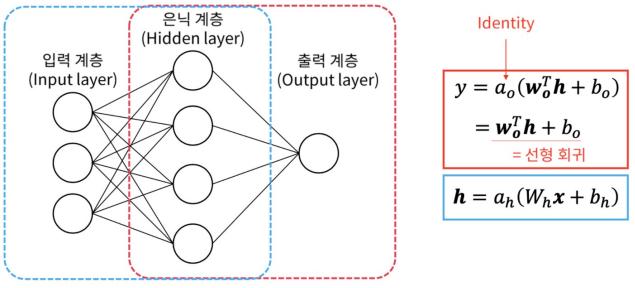
신경망의 회귀 : 얕은 신경망으로 회귀를 수행할 경우, 출력 계층은 선형 회귀와 동일하다. 입력 계층에서 은닉 계층으로 추가적인 변환이 있다는 것이 다르다
-
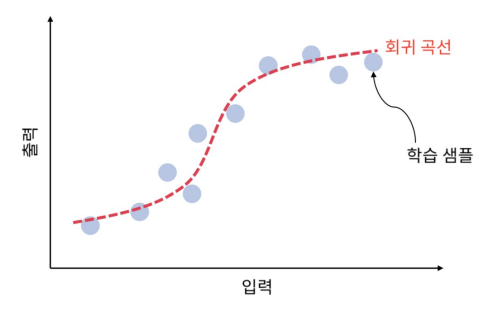
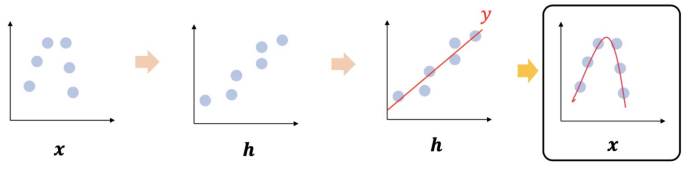
은닉층의 효과 : 선형적으로 분포되지 않는 입력 → 선형적으로 분포하는 은닉 계층(특징) → 선형회귀 입력 Space를 기준으로 보면 회귀 곡선이 된다
-
분류 : 입력의 범주를 추정하는 분류(Classification)
-
로지스틱 회귀(Logistion Regression) : 범주형 데이터를 대상으로 하는 회귀, 분류 기법으로 볼 수 있다. 로지스틱 회귀는 선형 회귀와 비슷하나, 범주형 데이터를 분류하는 방향으로 선을 긋는다

-
Sigmoid Function :
- 값이 작아질수록 0, 커질수록 1에 수렴
- 모든 실수 입력 값에 대해 출력이 정의됨
- 출력이 0 - 1 사이로, '확률'을 표현할 수 있음
- 입력 값이 0에 가까울수록 출력이 빠르게 변함
- 모든 점에서 미분 가능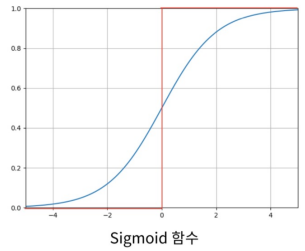
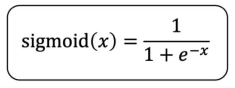
-
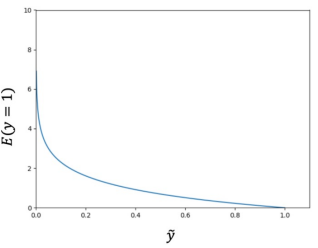
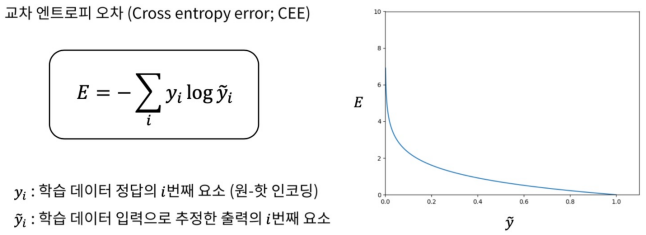
Cross Entoropy : 정확히 맞추면 오차가 0, 틀릴수록 오차가 무한히 증가하는 특징이 있다

-
다중 로지스틱 회귀의 기하학적 특징 : 변수가 하나 추가될 때마다 차원이 하나씩 추가된다. 직선 → 평면 → 초평면
-
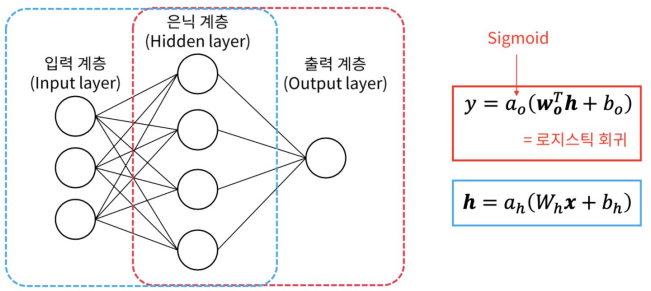
얇은 신경망과 이진 분류 : 얕은 신경망으로 Classification을 수행할 경우, 출력 계층은 로지스틱 회귀와 동일하다. 입력 계층에서 은닉 계층으로 추가적인 변환이 있다는 것만 다르다
-
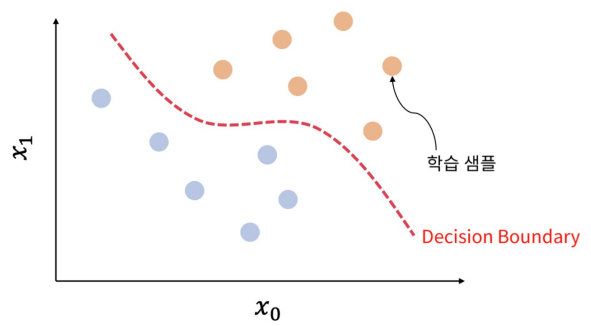
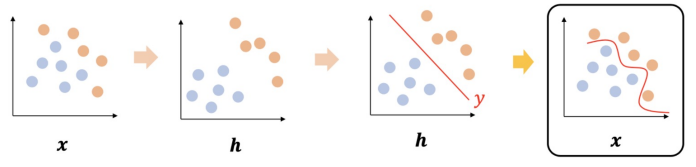
은닉계층과 분류 : 선형적으로 분리되지 않는 class → 선형적으로 분리되는 은닉 계층(특징) → 로지스틱 회귀 입력으로 Space를 기준으로 보면 Decision Boundary가 곡선이 된다
-
이진 분류에서는 '어떤 물체'인지 표현할 필요가 없으나, 다중 분류에서는 '어떤 물체'인지 표현해야 한다.
-
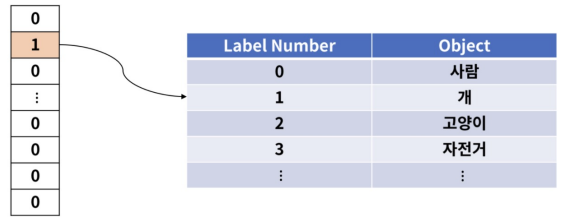
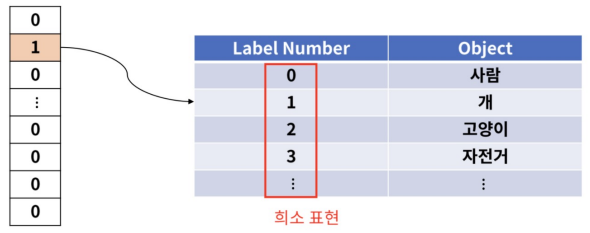
원 핫 인코딩(One-Hot Encoding) : 한 개의 값만 1이고, 나머지 값은 0인 벡터로 표현하는 기법. 원 핫 인코딩된 벡터는 미리 정해둔 Table을 이용해 어떤 물체인지 알 수 있다. (에러 크기를 동일하게..?..)
-
희소 행렬(Sparse Vector) : 대부분의 값이 0이고 크기가 있는 값이 희소하게 나타나는 벡터. 희소 표현을 이용해 벡터 전체를 표기하지 ㅇ낳고, 숫자 하나로 표현할 수 있다.
-
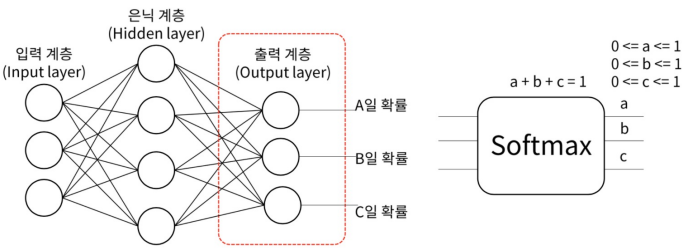
다중 클래스 : 한가지 확률만 100%이고 나머지는 0%인 것이 정답(= 원-핫 인코딩). 실제 알고리즘 출력을 확률로 변환하기 위해 Softmax 함수를 사용
-
Softmax : 최종 출력단에서 N가지 범주로 분류하는 Multi-class classification에 쓰임
- 각 입력의 지수함수를 정규화한 것
- 각 출력은 0 - 1 사이의 값을 가짐
- 모든 출력의 합이 반드시 1이 됨
- 여러 경우의 수 중 한가지에 속할 '확률'을 표현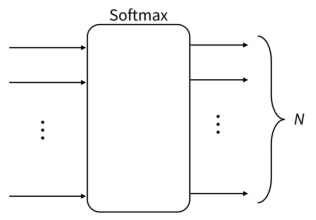
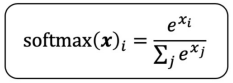
-
Softmax와 Sigmoid : Sigmoid는 하나의 입력을 0으로 강제한 2-Class Softmax 함수와 동일하다. 2가지 클래스로 구분하기 위해 1개의 입력을 받는다는 점에 주목

-
정답과 출력의 비교 : 원-핫 인코딩으로 인해, 정답인 클래스에 대해서만 오차를 계산. 정확히 맞추면 오차가 0, 틀릴수록 오차가 무한히 증가하는 특징이 있다
-
Cross Entropy Error : 오차를 내는 과정에서 정답 클래스만 비교하지만, 다중 클래스 분류의 활성함수인 Softmax로 인해 다른 클래스에 대한 학습에도 영향을 준다
💻 출처 : 제로베이스 데이터 취업 스쿨
