FUNDAMENTAL | 23. 활성화 함수의 이해

yeonk·2022년 2월 4일

aiffel-ai-bootcamp

목록 보기

36/38

💡Key Point💡
1. 활성화 함수
2. 선형과 비선형
3. 활성화 함수 종류

특정 조건(ex. 임계치) 만족 여부에 따라 활성화, 비활성화를 결정.
딥러닝 모델의 표현력을 향상을 위해 사용(representation capacity or expressivity)

선형 함수로는 비선형 함수를 표현할 수 없다.
모델의 파라미터와 입력값은 선형 관계
비선형 데이터를 표현하기 위해서는 모델이 비선형성을 가져야 함
비선형성을 위해 사용되는 것이 활성화 함수
선형 활성화 함수(Linear activation function), 비선형 활성화 함수(Non-linear activation function)로 나눌 수 있음

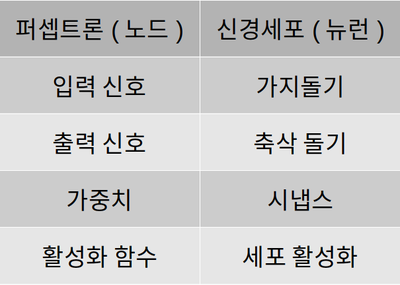
	출처: AIFFFEL FUNDAMENTALS_SSAC2 23. 활성화 함수의 이해

선형으로 $V$ 공간상의 벡터를 $W$ 공간상의 벡터로 바꿔주는 역할

$V$ , $W$ 에 대한 가정
- 모두 벡터 공간(≒좌표평면, 벡터를 그릴 수 있는 공간)
- 둘 모두 실수 집합상에 있다고 가정
- $V$ : 정의역(domain) 역할
- $W$ : 공역(codomain) 역할

선형변환의 조건 ( $T$ : $V$ → $W$ )
- 가산성(Additivity) : $x, y \in V$ 에 대하여
  $\mathcal{T}(x+y) =T(x)+T(y)$
- 동차성(Homogeneity) : $x \in V, c \in \Bbb{R}$ 에 대하여
  $\mathcal{T}(cx) = c\mathcal{T}(x)$

딥러닝 모델의 표현력을 향상

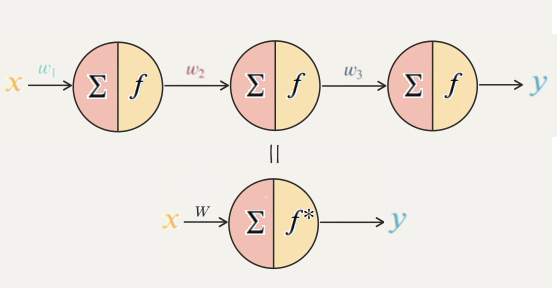
선형함수만 사용한다면? $y=f(w_3f(w_2f(w_1x)))$ $=f(w_3f(f(w_1w_2x)))$ $=f(f(f(w_1w_2w_3x)))$ $=f(f(f(Wx)))$

	AIFFEL FUNDAMENTALS_SSAC2 23. 활성화 함수의 이해

활성화 함수의 종류
- 이진 계단 함수(Binary step function)
- 선형 활성화 함수(Linear activation function)
- 비선형 활성화 함수(Non-linear activation function)

입력이 임계점을 넘으면 1(True)를 출력, 그렇지 않으면 0 출력

σ(x)= \frac{1}{1+e^{−x}}

0이 중심(zero-centered)이 아님
- upstream gradient의 부호에 따라 이 노드의 가중치는 모두 양의 방향으로 업데이트되거나, 모두 음의 방향으로 업데이트 → 훈련의 시간이 오래 걸림

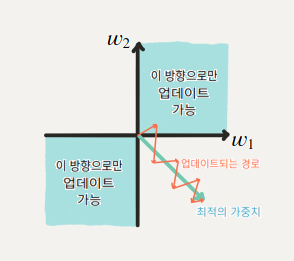
출처: AIFFEL FUNDAMENTALS_SSAC2 23. 활성화 함수의 이해

tanh(x)= \frac{e^x−e^{−x}}{e^x+e^{−x}}

f(x)=max(0,x)

최근 가장 많이 사용되고 있는 활성화 함수
탄젠트를 사용한 모델보다 몇 배 더 빠르게 훈련
비용이 높은 (예를 들면, exponential와 같은) 연산을 사용하지 않기 때문에 처리 속도가 빠름
ReLU는 0을 제외한 구간에서 미분이 가능
단점
- 출력값이 0이 중심이 아님
- Dying ReLU
  - 모델에서 ReLU를 사용한 노드가 비활성화되며 출력을 0으로만 하는 것
  - 노드의 출력값과 그래디언트가 0이 되어 노드가 죽어버리는 문제 (특히 학습률(learning rate)을 크게 잡을 때 자주 발생)