
20211108
1. 정보 이론(information theory)
추상적인 정보 개념을 정량화, 정보 저장과 통신 연구
-
: 사건 가 일어날 확률
-
: 정보량(information content)
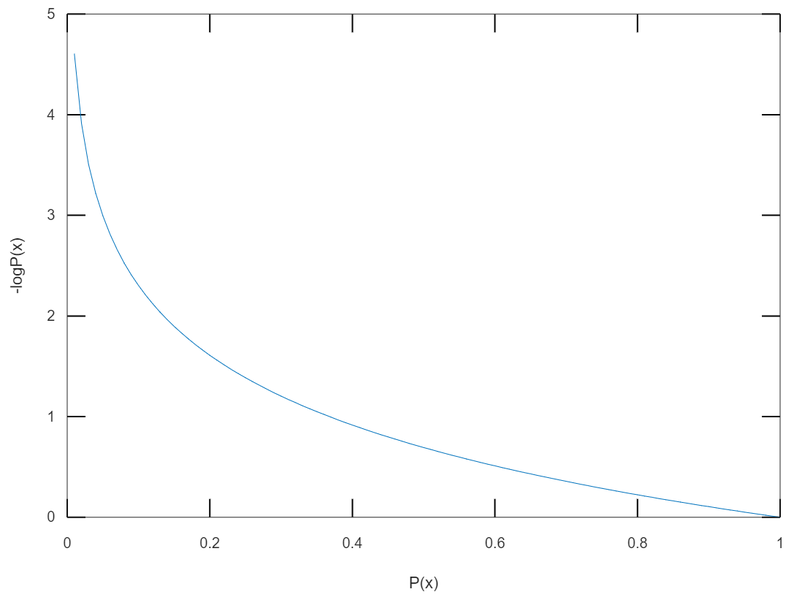
출처: AIFFEL FUNDAMENTALS_SSAC2 25. 정보이론 톺아보기-
일어날 가능성이 높은 사건일수록 정보량이 낮다.
-
일어날 가능성이 낮은 사건일수록 정보량이 높다.
-
전체 정보량 = 두 개의 독립 사건 정보량의 합
-
함수가 항상 양수인 이유는 확률의 범위가 [0, 1] 이기 때문이다.
2. 엔트로피(entropy)
특정 확률분포를 따르는 사건들의 정보량 기댓값.
무질서도 또는 불확실성과 비슷하다.
이산확률변수(discrete random variable) 경우
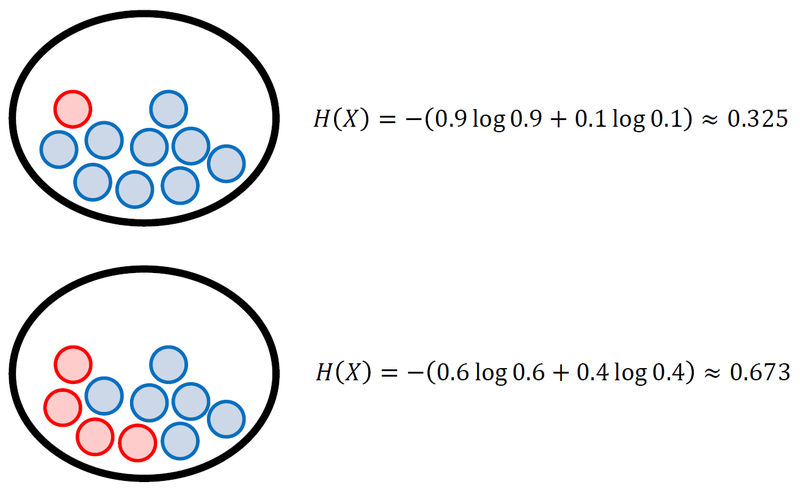
출처: AIFFEL FUNDAMENTALS_SSAC2 25. 정보이론 톺아보기-
확률 변수가 가질 수 있는 값의 가짓수가 같을 때, 확률이 균등할수록 엔트로피 값 증가
-
균등 분포(uniform distribution)일 때 엔트로피 값 최대
연속 확률 변수(Continuous Random Variables) 경우
- 미분 엔트로피(differential entropy)라고도 함
3. 쿨백-라이블러 발산(Kullback-Leibler divergence, KL divergence)
생성 모델을 학습시킬 때 두 확률 분포의 차이를 나타내는 지표.
-
머신러닝의 모델 종류
-
결정 모델(discriminative model): 결정 경계만 학습(데이터 실제 분포 모델링 X)
-
생성 모델(generative model): 데이터의 실제 분포를 간접적으로 모델링(여러 확률 분포와 베이즈 이론을 이용)
-
이산확률변수(discrete random variable) 경우
-
: 데이터가 따르는 실제 확률 분포
-
: 모델이 나타내는 확률 분포
-
KL divergence
-
의 평균 정보량과 의 평균 정보량의 차이
-
실제 확률 분포 대신 근사적인 분포를 사용했을 때 발생하는 엔트로피 변화량
-
위 식이 왜 저렇게 되는지 몰라서 설명듣고 적어봤다.
급하게 적어서 글씨가 너무 더럽네 😅
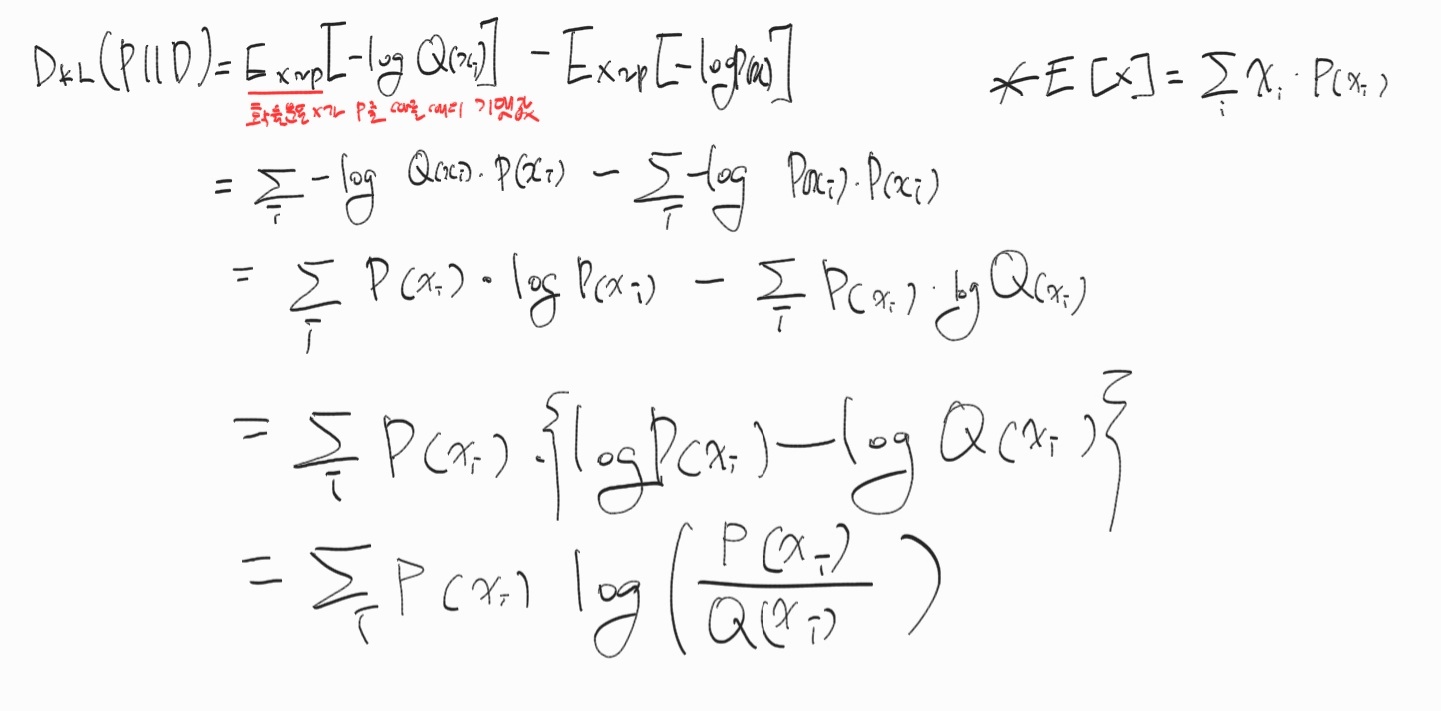
연속 확률 변수(Continuous Random Variables) 경우
KL divergence의 특성
-
-
if and only if
-
non-symmetric:
-ML에서는 최소화 방향으로 모델 학습
- 는 실제 값이라 변경 불가능 → $Q(x)를 최소화 하여 KL divergence를 최소화 하여야 한다.
교차 엔트로피(cross entropy)
P(x)를 기준으로 계산한 Q(x)의 엔트로피
엔트로피, 교차 엔트로피, KL divergence의 관계
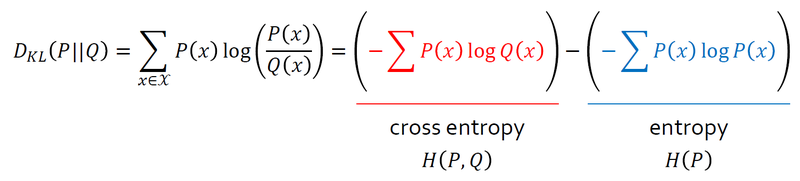
출처: AIFFEL FUNDAMENTALS_SSAC2 25. 정보이론 톺아보기
4. Cross Entropy Loss
-
분류 문제에서 데이터 라벨 → one-hot encoding로 표현
-
데이터가 n 번째 클래스에 속하면 n번째 원소만 1인 n차원 벡터로 !(나머지는 0)
예를 들어 3개의 클래스가 인 분류 문제가 있다.
의 값(출력값)이 이라고 가정해보자.
- 결과는 하기와 같이 나타낼 수 있다.
- 로 차이 구하기
- 로 차이를 구하면 계산이 간단하다.
Cross Entropy와 Likelihood
모델의 파라미터를 θ라고 해보자.
-
: 모델이 표현한 확률 분포 (likelihood와 같음)
-
: 데이터의 실제 분포
-
cross entropy 최소화 파라미터 구하기
= negative log likelihood 최소화 파라미터 구하기
5. Decision Tree와 Entropy
의사결정나무(Decision Tree)
엔트로피가 감소하면 그 만큼 정보 이득(Information Gain, IG)을 얻는다!
-
: 전체 사건의 집합
-
: 분류 기준으로 고려되는 속성(feature)의 집합
-
: 는 에 속하는 속성
-
: 속성을 가진 의 부분집합
-
: 집합 의 크기(원소의 개수)
-
: 라는 사건 집합이 지닌 엔트로피

블로그 정리 화이팅입니다!