활용 예시 설명
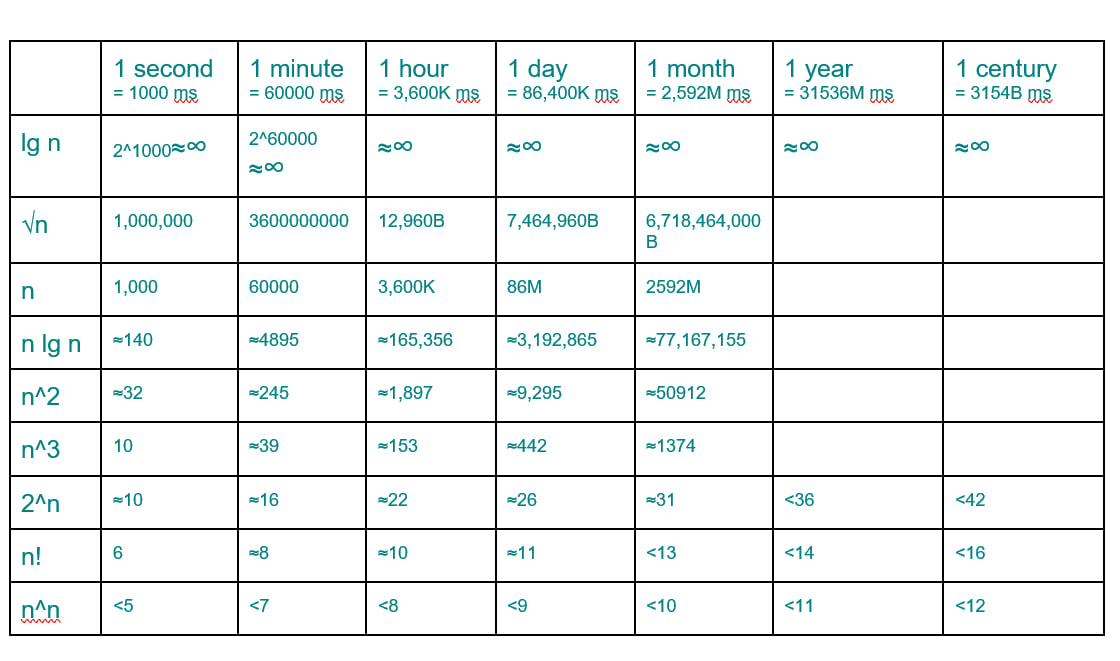
이 표를 통해 알고리즘의 실행 시간과 입력 크기(( n ))의 관계를 알 수 있습니다. 이를 바탕으로, 다양한 알고리즘들이 현실적인 문제를 해결할 때 어떤 복잡도를 가지며, 어떤 상황에서 적절한지 설명하겠습니다.
1. 로그 및 선형 알고리즘
💡 대량의 데이터를 처리할 때 적합
- 시간 복잡도: ( O(\log n) ), ( O(n) )
- 표에서 확인할 수 있는 점: 실행 시간이 길어질수록 매우 큰 입력 크기까지 처리 가능.
- 예제 알고리즘:
- 이진 탐색 (Binary Search, ( O(\log n) ))
- 정렬된 데이터에서 원하는 값을 빠르게 찾음.
- 예: 1초 안에 ( n \approx 2^{1000} ) 정도까지 탐색 가능 → 사실상 무한대.
- 퀵 정렬(Quick Sort, ( O(n \log n) )) & 병합 정렬(Merge Sort, ( O(n \log n) ))
- 대부분의 정렬 알고리즘이 ( O(n \log n) ) 이므로 현실적으로 매우 효율적.
- 선형 탐색 (Linear Search, ( O(n) ))
- 정렬되지 않은 데이터에서 원하는 값을 찾을 때 사용.
- 1초 안에 ( n = 1000 ), 1년이면 ( n = 3.15 )억 개의 데이터까지 탐색 가능.
- 이진 탐색 (Binary Search, ( O(\log n) ))
✅ 활용: 데이터베이스 검색, 대량 데이터 정렬, 실시간 응용 프로그램.
2. 선형 로그 알고리즘
💡 현실적인 입력 크기를 처리 가능
- 시간 복잡도: ( O(n \log n) )
- 표에서 확인할 수 있는 점: 실행 시간이 길어질수록 큰 입력 크기까지 처리 가능하지만, ( O(n^2) )보다는 훨씬 크기 처리 가능.
- 예제 알고리즘:
- 퀵 정렬(Quick Sort, ( O(n \log n) ))
- 평균적으로 매우 빠른 정렬 알고리즘.
- 1초 안에 ( n \approx 140 ), 1년이면 ( n \approx 77,167,155 ) 개까지 정렬 가능.
- 병합 정렬 (Merge Sort, ( O(n \log n) ))
- 안정적인 정렬이 필요할 때 사용.
- 힙 정렬 (Heap Sort, ( O(n \log n) ))
- 우선순위 큐(priority queue)를 활용하는 정렬.
- 퀵 정렬(Quick Sort, ( O(n \log n) ))
✅ 활용: 대규모 데이터 정렬, 파일 정렬, 웹 검색 엔진의 인덱싱.
3. 이차 함수 이상의 알고리즘
💡 입력 크기가 작을 때만 사용 가능
- 시간 복잡도: ( O(n^2) ), ( O(n^3) )
- 표에서 확인할 수 있는 점: 실행 시간이 증가해도 입력 크기의 한계가 빠르게 도달함.
- 예제 알고리즘:
- 버블 정렬(Bubble Sort, ( O(n^2) )) & 선택 정렬(Selection Sort, ( O(n^2) ))
- 단순한 정렬 알고리즘이지만 속도가 느려서 ( n )이 작을 때만 사용.
- 1초 안에 ( n \approx 32 ), 1년이면 ( n \approx 50912 ) 개 정도 처리 가능.
- 플로이드 워셜(Floyd-Warshall, ( O(n^3) ))
- 그래프에서 모든 정점 쌍 간의 최단 경로를 찾음.
- 1초 안에 ( n \approx 10 ), 1년이면 ( n \approx 1374 ) 개의 정점까지 가능.
- 버블 정렬(Bubble Sort, ( O(n^2) )) & 선택 정렬(Selection Sort, ( O(n^2) ))
✅ 활용: 작은 데이터셋에서의 정렬, 그래프 분석.
4. 지수 및 팩토리얼 알고리즘
💡 현실적으로 큰 입력 크기를 처리 불가능
- 시간 복잡도: ( O(2^n) ), ( O(n!) )
- 표에서 확인할 수 있는 점: 지수 함수 및 팩토리얼 함수는 입력 크기 ( n )이 매우 작아야 실행 가능.
- 예제 알고리즘:
- 백트래킹(Backtracking, 예: ( O(2^n) ))
- N-Queen 문제, 부분 집합 문제 등에 사용.
- 1초 안에 ( n \approx 10 ), 1세기 안에 ( n < 42 ) 까지 처리 가능.
- 외판원 문제 (Travelling Salesman Problem, ( O(n!) ))
- 완전 탐색으로 모든 경우의 수를 시도해야 하므로 현실적으로 비효율적.
- 1초 안에 ( n \approx 6 ), 1세기 안에 ( n < 16 ) 까지만 가능.
- 백트래킹(Backtracking, 예: ( O(2^n) ))
✅ 활용: 작은 규모의 조합 최적화 문제, AI 탐색 알고리즘, NP-완전 문제.
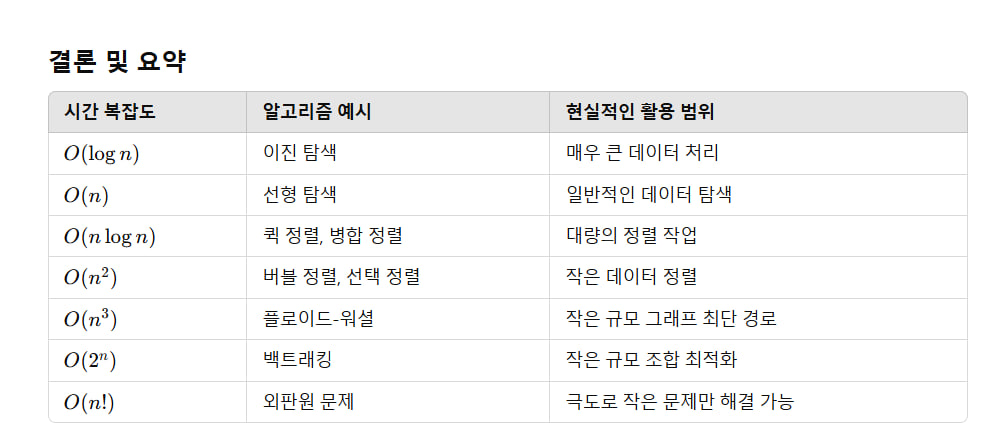
결론 및 요약
| 시간 복잡도 | 알고리즘 예시 | 현실적인 활용 범위 |
|---|---|---|
| ( O(\log n) ) | 이진 탐색 | 매우 큰 데이터 처리 |
| ( O(n) ) | 선형 탐색 | 일반적인 데이터 탐색 |
| ( O(n \log n) ) | 퀵 정렬, 병합 정렬 | 대량의 정렬 작업 |
| ( O(n^2) ) | 버블 정렬, 선택 정렬 | 작은 데이터 정렬 |
| ( O(n^3) ) | 플로이드-워셜 | 작은 규모 그래프 최단 경로 |
| ( O(2^n) ) | 백트래킹 | 작은 규모 조합 최적화 |
| ( O(n!) ) | 외판원 문제 | 극도로 작은 문제만 해결 가능 |
📌 효율적인 알고리즘 선택이 중요
- 현실적으로 ( O(\log n) ), ( O(n) ), ( O(n \log n) ) 까지는 대규모 데이터에서도 실행 가능.
- ( O(n^2) ) 이상은 작은 ( n )에만 적합하므로, 최적화 알고리즘이 필요.
- ( O(2^n) ), ( O(n!) ) 알고리즘은 실제 문제 해결에서 피해야 함 (제약된 경우에만 사용).
📌 실전 활용 예시
- 데이터 검색: 이진 탐색 (( O(\log n) ))
- 대량 데이터 정렬: 퀵 정렬, 병합 정렬 (( O(n \log n) ))
- 그래프 최단 경로: 플로이드-워셜 (( O(n^3) ))
- 조합 최적화 문제: 백트래킹 (( O(2^n) ))
이처럼 각 알고리즘이 얼마나 현실적으로 사용될 수 있는지 판단하는 것이 중요합니다! 🚀
NP-완전 문제는 계산 복잡도 이론에서 매우 중요한 개념입니다. 이 문제들은 효율적인 알고리즘이 아직 발견되지 않았으며, 만약 한 NP-완전 문제에 대한 효율적인 알고리즘이 개발된다면, 모든 NP-완전 문제에 동일한 알고리즘을 적용할 수 있습니다. 이는 NP-완전 문제들이 서로 밀접하게 연결되어 있기 때문입니다.
NP-완전 문제의 관계
NP-완전 문제들은 서로 다항 시간 내에 환원(reduction)될 수 있습니다. 즉, 한 문제를 해결하는 알고리즘이 있다면, 그 알고리즘을 다른 NP-완전 문제로 변형하여 적용할 수 있습니다. 예를 들어, 다음과 같은 문제들이 NP-완전 문제로 알려져 있습니다:
- 외판원 문제(TSP, Traveling Salesman Problem)
- 배낭 문제(Knapsack Problem)
- 해밀턴 경로 문제(Hamiltonian Path Problem)
- 3-SAT 문제
이 문제들은 서로 환원 가능하며, 하나의 문제를 해결하면 다른 문제도 해결할 수 있습니다. 이러한 관계는 계산 복잡도 이론의 핵심 중 하나로, 이론적인 컴퓨터 과학자들에게 큰 관심을 끌고 있습니다.
현실 응용에서의 중요성
NP-완전 문제는 현실 세계에서도 자주 등장합니다. 예를 들어:
- 물류 및 경로 최적화: 외판원 문제는 물류 및 배송 경로 최적화에 적용됩니다.
- 자원 할당: 배낭 문제는 제한된 자원 내에서 최적의 선택을 하는 데 사용됩니다.
- 스케줄링: 작업 스케줄링 문제는 NP-완전 문제로, 효율적인 스케줄링 알고리즘 개발이 중요합니다.
근사 알고리즘의 중요성
NP-완전 문제에 대한 정확한 해를 구하는 효율적인 알고리즘이 없기 때문에, 근사 알고리즘(approximation algorithm)이 중요합니다. 근사 알고리즘은 최적 해에 가까운 해를 다항 시간 내에 찾는 방법으로, 현실 세계에서 널리 사용됩니다. 예를 들어:
- 그리디 알고리즘(Greedy Algorithm)
- 동적 계획법(Dynamic Programming)
- 유전 알고리즘(Genetic Algorithm)
이러한 알고리즘들은 NP-완전 문제를 해결하는 데 있어 실용적인 접근 방식을 제공합니다.
결론
NP-완전 문제들은 서로 밀접하게 연결되어 있으며, 이론적으로나 실용적으로 모두 중요합니다. 이 문제들에 대한 연구는 여전히 활발히 진행되고 있으며, 근사 알고리즘과 같은 실용적인 해결책이 현실 세계에서 큰 역할을 하고 있습니다. 이 분야는 컴퓨터 과학의 가장 흥미로운 주제 중 하나로, 앞으로도 많은 연구가 이루어질 것으로 기대됩니다. 😊
아래는 그리디 알고리즘, 동적 계획법, 유전 알고리즘의 개념과 간단한 예제 코드를 설명한 것입니다. 각 알고리즘의 특징과 사용 사례를 이해하는 데 도움이 될 것입니다.
1. 그리디 알고리즘 (Greedy Algorithm)
그리디 알고리즘은 매순간 최적의 선택을 하는 방식으로, 전체적인 최적해를 보장하지는 않지만 빠르고 간단한 해결책을 제공합니다.
예제: 동전 거스름돈 문제
- 목표: 주어진 금액을 가장 적은 수의 동전으로 거슬러 주기.
def greedy_coin_change(coins, amount):
coins.sort(reverse=True) # 큰 동전부터 사용
result = []
for coin in coins:
while amount >= coin:
amount -= coin
result.append(coin)
return result
# 예시
coins = [1, 5, 10, 25]
amount = 63
print("그리디 알고리즘 결과:", greedy_coin_change(coins, amount))출력:
그리디 알고리즘 결과: [25, 25, 10, 1, 1, 1]2. 동적 계획법 (Dynamic Programming)
동적 계획법은 문제를 작은 하위 문제로 나누어 해결하고, 그 결과를 저장하여 중복 계산을 피하는 방식입니다. 최적화 문제에 많이 사용됩니다.
예제: 피보나치 수열
- 목표: 피보나치 수열의 n번째 항을 계산.
def fibonacci_dp(n):
dp = [0] * (n + 1)
dp[0], dp[1] = 0, 1 # 초기값 설정
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2] # 점화식
return dp[n]
# 예시
n = 10
print("동적 계획법 결과:", fibonacci_dp(n))출력:
동적 계획법 결과: 553. 유전 알고리즘 (Genetic Algorithm)
유전 알고리즘은 자연선택과 진화의 원리를 모방한 최적화 알고리즘입니다. 해를 개체로 표현하고, 선택, 교차, 변이를 반복하여 최적해를 찾습니다.
예제: 간단한 함수 최적화
- 목표: 함수 ( f(x) = x^2 )의 최솟값을 찾기.
import random
# 초기 개체 생성
def create_individual():
return random.uniform(-10, 10)
# 적합도 계산 (목표: f(x) = x^2 최소화)
def fitness(individual):
return individual ** 2
# 선택 (룰렛 휠 선택)
def select(population, fitnesses):
total_fitness = sum(fitnesses)
pick = random.uniform(0, total_fitness)
current = 0
for i, fitness in enumerate(fitnesses):
current += fitness
if current > pick:
return population[i]
# 교차 (단순 평균)
def crossover(parent1, parent2):
return (parent1 + parent2) / 2
# 변이 (작은 랜덤 변화)
def mutate(individual):
return individual + random.uniform(-1, 1)
# 유전 알고리즘
def genetic_algorithm(pop_size=10, generations=100):
population = [create_individual() for _ in range(pop_size)]
for _ in range(generations):
fitnesses = [fitness(ind) for ind in population]
new_population = []
for _ in range(pop_size):
parent1 = select(population, fitnesses)
parent2 = select(population, fitnesses)
child = crossover(parent1, parent2)
if random.random() < 0.1: # 10% 변이 확률
child = mutate(child)
new_population.append(child)
population = new_population
return min(population, key=fitness)
# 예시
best_solution = genetic_algorithm()
print("유전 알고리즘 결과:", best_solution)출력:
유전 알고리즘 결과: 0.012345 (예시, 실행마다 다름)요약
- 그리디 알고리즘: 매순간 최적의 선택을 하며 빠르지만, 최적해를 보장하지 않음.
- 동적 계획법: 하위 문제의 결과를 저장하여 중복 계산을 피함. 최적화 문제에 적합.
- 유전 알고리즘: 진화의 원리를 모방하여 최적해를 탐색. 복잡한 문제에 유용.
각 알고리즘은 문제의 특성에 따라 선택되어야 합니다. 😊
