BeingRichardFeynman

탁가이버·2025년 2월 23일

Algorithm

목록 보기

3/6

리처드 파인만(Richard Feynman)의 방식으로 시각화를 곁들여 설명해보겠습니다. 파인만은 복잡한 개념을 간단하고 직관적으로 설명하는 데 능했죠. 이제 각 알고리즘의 시간 복잡도를 시각화하고, 왜 특정 알고리즘이 현실적으로 사용 가능한지 또는 피해야 하는지 설명하겠습니다.

1. 시간 복잡도 시각화

아래는 각 시간 복잡도 ( O(log n) ), ( O(n) ), ( O(n log n) ), ( O(n^2) ), ( O(2^n) ), ( O(n!) )의 성장 속도를 시각화한 것입니다.

n       log n     n       n log n     n^2      2^n      n!
------------------------------------------------------------
1       0         1       0           1        2        1
2       1         2       2           4        4        2
4       2         4       8           16       16       24
8       3         8       24          64       256      40320
16      4         16      64          256      65536    2.09e+13
32      5         32      160         1024     4.29e+9  2.63e+35

( O(log n) ): 매우 느리게 증가합니다. 데이터가 10억 개여도 ( log n )은 약 30입니다.
( O(n) ): 선형적으로 증가합니다. 데이터가 10억 개면 10억 번 연산이 필요합니다.
( O(n log n) ): ( n )보다 조금 빠르게 증가하지만, 여전히 대규모 데이터에 적합합니다.
( O(n^2) ): 데이터가 1,000개면 100만 번 연산이 필요합니다. 10,000개는 1억 번 연산!
( O(2^n) ): 데이터가 30개만 되어도 10억 번 이상의 연산이 필요합니다.
( O(n!) ): 데이터가 20개만 되어도 ( 2.43 times 10^{18} )번 연산이 필요합니다. (현실적으로 불가능)

2. 실전 활용 예시와 시각화

(1) 데이터 검색: 이진 탐색 ( O(log n) )

시각화: 전화번호부에서 이름을 찾는 것과 같습니다. 반으로 나누어 찾기 때문에 매우 빠릅니다.

코드:

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
target = 5
print("이진 탐색 결과:", binary_search(arr, target))

(2) 대량 데이터 정렬: 퀵 정렬 ( O(n log n) )

시각화: 카드를 빠르게 정렬하는 것과 같습니다. 피벗을 기준으로 작은 값과 큰 값을 나누고, 재귀적으로 정렬합니다.

코드:

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

arr = [3, 6, 8, 10, 1, 2, 1]
print("퀵 정렬 결과:", quicksort(arr))

(3) 그래프 최단 경로: 플로이드-워셜 ( O(n^3) )

시각화: 모든 도시 사이의 최단 경로를 계산하는 것과 같습니다. 3중 반복문을 사용하므로 ( n^3 )의 시간이 걸립니다.

코드:

def floyd_warshall(graph):
    n = len(graph)
    dist = [row[:] for row in graph]  # 초기 거리 행렬 복사
    for k in range(n):
        for i in range(n):
            for j in range(n):
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
    return dist

graph = [
    [0, 5, float('inf'), 10],
    [float('inf'), 0, 3, float('inf')],
    [float('inf'), float('inf'), 0, 1],
    [float('inf'), float('inf'), float('inf'), 0]
]
print("플로이드-워셜 결과:", floyd_warshall(graph))

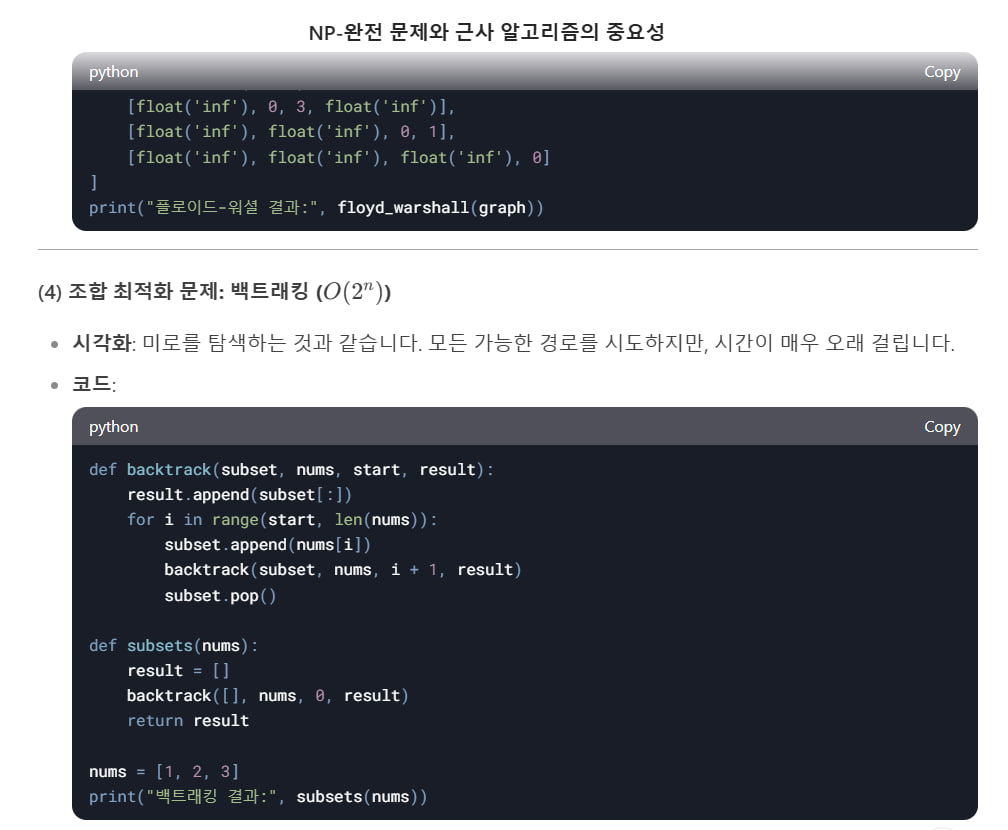
(4) 조합 최적화 문제: 백트래킹 ( O(2^n) )

시각화: 미로를 탐색하는 것과 같습니다. 모든 가능한 경로를 시도하지만, 시간이 매우 오래 걸립니다.

코드:

def backtrack(subset, nums, start, result):
    result.append(subset[:])
    for i in range(start, len(nums)):
        subset.append(nums[i])
        backtrack(subset, nums, i + 1, result)
        subset.pop()

def subsets(nums):
    result = []
    backtrack([], nums, 0, result)
    return result

nums = [1, 2, 3]
print("백트래킹 결과:", subsets(nums))

3. 왜 ( O(n^2) ) 이상은 피해야 할까?

( O(n^2) ): 데이터가 10,000개면 1억 번 연산이 필요합니다. 현대 컴퓨터로는 가능하지만, 데이터가 더 커지면 문제가 됩니다.
( O(2^n) ): 데이터가 30개만 되어도 10억 번 이상의 연산이 필요합니다. 현실적으로 불가능합니다.
( O(n!) ): 데이터가 20개만 되어도 ( 2.43 times 10^{18} )번 연산이 필요합니다. 우주 전체의 컴퓨터를 동원해도 해결할 수 없습니다.

4. 결론

( O(log n) ), ( O(n) ), ( O(n log n) ): 대규모 데이터에서도 사용 가능합니다.
( O(n^2) ): 작은 데이터에만 적합합니다.
( O(2^n) ), ( O(n!) ): 현실적으로 사용 불가능합니다.

알고리즘을 선택할 때는 문제의 크기와 시간 복잡도를 고려해야 합니다. 파인만처럼 시각화하고 직관적으로 이해하면 더 쉽게 선택할 수 있습니다! 😊

알고리즘을 현실적으로 사용 가능한지 빠르게 판단하는 방법은 입력 크기( ( n ) )에 따른 실행 가능 여부를 직관적으로 파악하는 것입니다. 이를 위해 다음과 같은 방법을 사용할 수 있습니다.

1. 실행 시간 한계 계산 (Thumb Rule)

💡 기본적으로 1초에 10⁸ (100,000,000) 번 연산 가능
컴퓨터가 보통 1초에 약 ( 10^8 ) 개의 기본 연산(덧셈, 곱셈 등)을 처리할 수 있다고 가정하고, 이를 기반으로 알고리즘의 시간 복잡도가 현실적으로 실행 가능한지 판단할 수 있습니다.

시간 복잡도	실행 가능한 최대 입력 크기 ( n ) (약 1초 기준)
( O(1) )	언제나 빠름
( O(log n) )	( n \approx 2^{10^8} ) → 사실상 무한대
( O(n) )	( n \approx 10^8 )
( O(n log n) )	( n \approx 10^7 )
( O(n^2) )	( n \approx 10^4 )
( O(n^3) )	( n \approx 500 )
( O(2^n) )	( n \approx 25 )
( O(n!) )	( n \approx 12 )

✅ 활용 방법
1. 주어진 입력 크기 ( n ) 확인
2. 해당 알고리즘의 시간 복잡도를 위 표와 비교
3. 실행 가능 여부 판단

( n )이 한계보다 작으면 실행 가능
한계를 초과하면 다른 알고리즘 고려

예제 1: ( n = 10^6 ), 알고리즘이 ( O(n^2) ) 일 때?
→ 위 표에서 ( O(n^2) ) 은 최대 ( n \approx 10^4 ) 까지 실행 가능.
→ 불가능하므로 개선 필요 (예: ( O(n log n) ) 알고리즘으로 변경).

예제 2: ( n = 1000 ), 알고리즘이 ( O(n^3) ) 일 때?
→ 위 표에서 ( O(n^3) ) 은 ( n \approx 500 ) 까지 가능.
→ 약간 위험하지만 가능할 수도 있음 (빠른 컴퓨터라면 OK).

2. 간단한 백오브더넵킨(Back of the Napkin) 계산

시간을 대략적으로 계산해보는 방법도 있습니다.

기본적으로 1초 ≈ ( 10^8 ) 연산 가능
알고리즘이 ( O(n^2) ) 이면 필요한 연산량 ≈ ( n^2 )
( n = 10^6 ) 이라면, 필요 연산량 = ( 10^{12} ) 연산
1초에 ( 10^8 ) 연산이므로, 약 ( 10^4 ) 초 ≈ 3시간 소요
- 즉, 너무 오래 걸려서 비현실적!

✅ 활용 방법
1. 기본적인 연산 한도( ( 10^8 ) 연산/초 )를 기억
2. 알고리즘의 복잡도에 따라 연산량 추정
3. 1초 안에 가능한지 비교하여 실행 가능 여부 판단

3. 알고리즘 개선 가능 여부 체크

만약 현재 알고리즘이 너무 느리다면, 아래 방법을 고려하세요.

1) 시간 복잡도 개선

( O(n^2) ) → ( O(n \log n) )
- 예: 버블 정렬 ( O(n^2) ) → 퀵 정렬 ( O(n \log n) )
( O(n!) ) → ( O(2^n) ) → ( O(n^3) )
- 예: 완전 탐색 대신 동적 계획법 사용

2) 적절한 알고리즘 선택

데이터가 거의 정렬되어 있음? → 삽입 정렬 ( O(n) )
최단 경로 문제? → 다익스트라 ( O(E log V) )
그래프 탐색? → DFS/BFS ( O(V+E) )

4. 현실적 판단을 위한 정리

( O(n log n) ) 이하면 대부분 현실적으로 실행 가능
( O(n^2) ) 이상이면 ( n )이 작을 때만 실행 가능
( O(2^n) ), ( O(n!) ) 은 매우 작은 ( n )에서만 사용
1초 ≈ ( 10^8 ) 연산 가능을 기준으로 대략적인 계산

✅ 실제 프로그래밍 대회나 코딩 테스트에서도 이 기준을 사용하여 알고리즘을 선택합니다! 🚀

This Python code defines several functions for sorting, searching, and binary addition. Let’s break it down step by step:

1. `insertion_sort_ascending(numbers)`

This function sorts a list of numbers in ascending order using the insertion sort algorithm.

How it works:

Iterate through the list starting from the second element (i ranges from 1 to len(numbers) - 1).
For each element at index i, compare it with the previous elements (j ranges from i to 0 in reverse).
If the previous element (numbers[j - 1]) is greater than the current element (numbers[j]), swap them using the swap function.
Repeat until the list is sorted.

Example:

Input: [54, 3, 91, 40, 21, 8, 19, 40]
Output: [3, 8, 19, 21, 40, 40, 54, 91]

2. `insertion_sort_descending(numbers)`

This function sorts a list of numbers in descending order using the insertion sort algorithm.

How it works:

Similar to insertion_sort_ascending, but the comparison is reversed.
If the previous element (numbers[j - 1]) is less than the current element (numbers[j]), swap them.

Example:

Input: [54, 3, 91, 40, 21, 8, 19, 40]
Output: [91, 54, 40, 40, 21, 19, 8, 3]

3. `swap(array, idx_a, idx_b)`

This helper function swaps two elements in a list at indices idx_a and idx_b.

How it works:

Store the value at idx_a in a temporary variable tmp.
Assign the value at idx_b to idx_a.
Assign the value of tmp to idx_b.

4. `linear_search(numbers, value)`

This function performs a linear search to find the index of a given value in a list.

How it works:

Iterate through the list.
If the current element matches the value, return its index.
If the value is not found, return None.

Example:

Input: [3, 8, 19, 21, 40, 40, 54, 91], value = 41
Output: None (since 41 is not in the list).

5. `add_two_bin_numbers(array_a, array_b, size)`

This function adds two binary numbers represented as lists of bits (0s and 1s).

How it works:

Start from the least significant bit (end of the list) and move towards the most significant bit (start of the list).
Add the corresponding bits from array_a and array_b, along with any carry-over from the previous addition.
If the sum of the bits is greater than 1, set the carry-over to 1 and store the sum modulo 2 in the result.
If the sum is 1 or 0, store the sum directly and set the carry-over to 0.
Insert the final carry-over at the beginning of the result list.

Example:

Input: array_a = [1, 0, 1, 0], array_b = [1, 1, 1, 0]
Output: [1, 1, 0, 0, 0] (binary addition of 1010 + 1110 = 11000).

6. Test Data and Output

The code tests the functions with the following steps:

Sorting:
- Sorts inputData in ascending order and prints the result.
- Sorts inputData in descending order and prints the result.
Searching:
- Searches for the value 41 in the sorted list and prints the result.
Binary Addition:
- Adds two binary numbers [1, 0, 1, 0] and [1, 1, 1, 0] and prints the result.

Output of the Code

inputData (ascending) =  [3, 8, 19, 21, 40, 40, 54, 91]
inputData (descending) =  [91, 54, 40, 40, 21, 19, 8, 3]
search result =  None
sum =  [1, 1, 0, 0, 0]

Key Observations

The insertion sort implementation has a bug in the inner loop:
- The inner loop should stop at j > 0 instead of j >= 0. Otherwise, it will cause an IndexError when j = 0.
- Fix: Change for j in range(i, 0, -1) to for j in range(i, 0, -1).
The binary addition function works correctly but uses insert(0, ...) to prepend bits, which is inefficient for large lists. Using a list and reversing it at the end would be more efficient.
The linear search function works as expected but could be optimized for sorted lists using binary search.

Let me know if you need further clarification! 😊

참조: 파인만 도형(Feynman Diagram)은 물리학자 리처드 파인만(Richard Feynman)이 양자 전기역학(QED, Quantum Electrodynamics)을 설명하기 위해 개발한 시각적 도구입니다. 이 도형은 입자 물리학에서 입자 간의 상호작용을 직관적으로 표현하며, 복잡한 수학적 계산을 간단히 시각화하는 데 사용됩니다.

1. 파인만 도형의 목적

입자 간의 상호작용을 시각적으로 표현합니다.
복잡한 수학적 계산을 단순화하고 직관적으로 이해할 수 있게 합니다.
양자장 이론(QFT, Quantum Field Theory)에서 중요한 역할을 합니다.

2. 파인만 도형의 기본 요소

파인만 도형은 다음과 같은 요소로 구성됩니다:

(1) 입자 선 (Particle Lines)

실선: 전자, 양성자 등 물질 입자를 나타냅니다.
물결선: 광자(photon)와 같은 파동 입자를 나타냅니다.
점선: 글루온(gluon)과 같은 다른 입자를 나타낼 수도 있습니다.

(2) 정점 (Vertex)

입자 간의 상호작용이 일어나는 지점을 나타냅니다.
예: 전자와 광자가 상호작용하는 지점.

(3) 시간 축

도형의 왼쪽에서 오른쪽으로 시간이 흐릅니다.
입자의 생성, 소멸, 상호작용을 시간 순서대로 표현합니다.

3. 파인만 도형의 예시

(1) 전자-광자 산란 (Compton Scattering)

전자와 광자가 충돌하여 에너지를 교환하는 과정.

파인만 도형:

e⁻  ------>  ●
             / \
            /   \
γ  -------->     ●  ------>  e⁻

(2) 전자-양전자 쌍 생성 (Pair Production)

광자가 전자와 양전자 쌍을 생성하는 과정.

파인만 도형:

γ  -------->  ●
             / \
            /   \
e⁻  <------ ●  ------>  e⁺

(3) 전자-전자 산란 (Electron-Electron Scattering)

두 전자가 광자를 교환하며 상호작용하는 과정.

파인만 도형:

e⁻  ------>  ●  <------  e⁻
             |
             |
             γ
             |
             |
e⁻  <------  ●  ------>  e⁻

4. 파인만 도형의 장점

직관적 이해: 복잡한 수학적 계산을 시각적으로 표현하여 이해하기 쉽습니다.
계산 단순화: 도형을 통해 적분과 같은 복잡한 계산을 단순화할 수 있습니다.
물리적 통찰: 입자 간의 상호작용을 명확히 보여줍니다.

5. 파인만 도형의 한계

고차원 상호작용을 표현하기에는 복잡해질 수 있습니다.
모든 물리적 현상을 완벽히 설명하지는 못합니다.

6. 결론

파인만 도형은 양자 물리학의 복잡한 개념을 직관적으로 이해하는 데 매우 유용한 도구입니다. 리처드 파인만은 이 도형을 통해 양자 전기역학의 계산을 단순화하고, 물리학자들이 입자 상호작용을 쉽게 이해할 수 있도록 도왔습니다. 이 도형은 물리학뿐만 아니라 과학 전반에서 시각화의 중요성을 보여주는 대표적인 예입니다. 😊

탁가이버

더 나은 세상은 가능하다를 믿고 실천하는 활동가

이전 포스트

NPcomplete

다음 포스트

BeingRichardFeynman

Algorithm

1. 시간 복잡도 시각화

2. 실전 활용 예시와 시각화

(1) 데이터 검색: 이진 탐색 ( O(log n) )

(2) 대량 데이터 정렬: 퀵 정렬 ( O(n log n) )

(3) 그래프 최단 경로: 플로이드-워셜 ( O(n^3) )

(4) 조합 최적화 문제: 백트래킹 ( O(2^n) )

3. 왜 ( O(n^2) ) 이상은 피해야 할까?

4. 결론

1. 실행 시간 한계 계산 (Thumb Rule)

2. 간단한 백오브더넵킨(Back of the Napkin) 계산

3. 알고리즘 개선 가능 여부 체크

1) 시간 복잡도 개선

2) 적절한 알고리즘 선택

4. 현실적 판단을 위한 정리

1. insertion_sort_ascending(numbers)

How it works:

Example:

2. insertion_sort_descending(numbers)

How it works:

Example:

3. swap(array, idx_a, idx_b)

How it works:

4. linear_search(numbers, value)

How it works:

Example:

5. add_two_bin_numbers(array_a, array_b, size)

How it works:

Example:

6. Test Data and Output

Output of the Code

Key Observations

1. 파인만 도형의 목적

2. 파인만 도형의 기본 요소

(1) 입자 선 (Particle Lines)

(2) 정점 (Vertex)

(3) 시간 축

3. 파인만 도형의 예시

(1) 전자-광자 산란 (Compton Scattering)

(2) 전자-양전자 쌍 생성 (Pair Production)

(3) 전자-전자 산란 (Electron-Electron Scattering)

4. 파인만 도형의 장점

5. 파인만 도형의 한계

6. 결론

NPcomplete

MergeSort

0개의 댓글

1. `insertion_sort_ascending(numbers)`

2. `insertion_sort_descending(numbers)`

3. `swap(array, idx_a, idx_b)`

4. `linear_search(numbers, value)`

5. `add_two_bin_numbers(array_a, array_b, size)`