MergeSort

탁가이버·2025년 2월 24일

Algorithm

목록 보기

4/6

이제 문제를 더 단순화하여 설명하겠습니다. 우리가 정말로 관심 있는 것은 알고리즘의 실행 시간이 얼마나 빠르게 증가하는지, 즉 성장률(order of growth)입니다. 따라서 우리는 공식에서 가장 중요한 항만 고려합니다. 예를 들어, ( an^2 )와 같은 항에서 낮은 차수의 항(예: ( bn + c ))은 큰 ( n ) 값에 대해 상대적으로 중요하지 않습니다. 또한, 가장 높은 차수 항의 상수 계수도 무시합니다. 왜냐하면 큰 입력 크기에서 계산 효율성을 결정하는 데는 성장률이 상수 계수보다 훨씬 더 중요하기 때문입니다.

예를 들어, 삽입 정렬(insertion sort)의 최악의 경우 실행 시간을 고려할 때, 낮은 차수의 항과 상수 계수를 무시하면 ( n^2 ) 항만 남습니다. 이 ( n^2 ) 항이 실행 시간에서 가장 중요한 부분입니다. 예를 들어, 어떤 알고리즘이 특정 컴퓨터에서 ( \frac{n^2}{100} + 100n + 17 ) 마이크로초가 걸린다고 가정해봅시다. ( n^2 ) 항의 계수인 ( \frac{1}{100} )과 ( n ) 항의 계수인 ( 100 )은 크게 차이가 나지만, ( n )이 10,000을 넘어가면 ( \frac{n^2}{100} ) 항이 ( 100n ) 항을 압도합니다. 10,000은 평균적인 마을 인구보다 작은 숫자이며, 실제 문제에서는 훨씬 더 큰 입력 크기가 자주 발생합니다.

이러한 성장률을 강조하기 위해 우리는 그리스 문자 ( \Theta ) (세타)를 사용한 특별한 표기법을 사용합니다. 예를 들어, 삽입 정렬의 최악의 경우 실행 시간을 ( \Theta(n^2) )라고 씁니다. 이는 "큰 ( n )에 대해 대략 ( n^2 )에 비례한다"는 의미입니다. 마찬가지로, 삽입 정렬의 최선의 경우 실행 시간은 ( \Theta(n) )입니다.

일반적으로, 한 알고리즘이 다른 알고리즘보다 더 효율적이라고 여겨지는 경우는 최악의 경우 실행 시간의 성장률이 더 낮을 때입니다. 상수 계수와 낮은 차수의 항 때문에, 성장률이 더 높은 알고리즘이 작은 입력에 대해서는 더 빠를 수 있습니다. 그러나 충분히 큰 입력 크기 ( n )에 대해서는 ( \Theta(n^2) ) 알고리즘이 ( \Theta(n^3) ) 알고리즘보다 항상 더 빠릅니다.

연습 문제

2.2-1

함수 ( \frac{n^3}{1000} + 100n^2 - 100n + 3 )을 ( \Theta )-표기법으로 표현하시오.

답:
( \Theta(n^3) )

2.2-2

배열 ( A[1 : n] )에 저장된 ( n )개의 숫자를 정렬하는 문제를 고려하시오. 먼저 ( A[1 : n] )에서 가장 작은 요소를 찾아 ( A[1] )과 교환합니다. 그 다음 ( A[2 : n] )에서 가장 작은 요소를 찾아 ( A[2] )와 교환합니다. 이 과정을 ( A )의 첫 ( n-1 )개 요소에 대해 반복합니다. 이 알고리즘을 선택 정렬(selection sort)이라고 합니다. 이 알고리즘의 의사코드를 작성하고, 어떤 루프 불변식(loop invariant)을 유지하는지 설명하시오. 또한, 왜 이 알고리즘이 모든 ( n )개 요소가 아닌 첫 ( n-1 )개 요소에 대해서만 실행되는지 설명하시오. 선택 정렬의 최악의 경우 실행 시간을 ( \Theta )-표기법으로 표현하시오. 최선의 경우 실행 시간은 더 나은가요?

답:

의사코드:

SELECTION-SORT(A):
    for i = 1 to n-1:
        min_idx = i
        for j = i+1 to n:
            if A[j] < A[min_idx]:
                min_idx = j
        swap(A[i], A[min_idx])

루프 불변식:
각 반복이 시작될 때, ( A[1 : i-1] )은 정렬되어 있으며, 이 부분 배열은 전체 배열에서 가장 작은 ( i-1 )개의 요소를 포함합니다.
왜 ( n-1 )개 요소만 정렬하는가?
마지막 요소는 이미 정렬된 상태이므로 추가적인 정렬이 필요하지 않습니다.
최악의 경우 실행 시간:
( \Theta(n^2) )
최선의 경우 실행 시간:
( \Theta(n^2) ) (최선의 경우와 최악의 경우가 동일합니다.)

2.2-3

선형 탐색(linear search)을 다시 고려하시오 (연습 문제 2.1-4 참조). 평균적으로 입력 배열의 몇 개 요소를 검사해야 하는가? (찾는 요소가 배열의 어떤 요소와도 동일할 가능성이 동일하다고 가정합니다.) 최악의 경우에는 몇 개의 요소를 검사해야 하는가? ( \Theta )-표기법을 사용하여 선형 탐색의 평균 및 최악의 경우 실행 시간을 표현하시오. 답을 정당화하시오.

답:

평균적으로 검사하는 요소의 수:
( \frac{n}{2} ) (평균적으로 배열의 절반을 검사합니다.)
최악의 경우 검사하는 요소의 수:
( n ) (찾는 요소가 배열의 마지막에 있거나 없는 경우)
평균 실행 시간:
( \Theta(n) )
최악의 실행 시간:
( \Theta(n) )

2.2-4

어떤 정렬 알고리즘이든 최선의 경우 실행 시간을 개선하기 위해 어떻게 수정할 수 있는가?

답:
알고리즘이 이미 정렬된 입력에 대해 빠르게 동작하도록 특수한 조건을 추가합니다. 예를 들어, 입력이 이미 정렬된 경우 알고리즘이 바로 종료하도록 할 수 있습니다.

2.3 알고리즘 설계

알고리즘 설계에는 다양한 기법이 있습니다. 삽입 정렬은 증분 방법(incremental method)을 사용합니다: 각 요소 ( A[i] )를 이미 정렬된 부분 배열 ( A[1 : i-1] )에 삽입합니다.

이 섹션에서는 분할 정복(divide-and-conquer)이라는 설계 방법을 살펴봅니다. 이 방법은 문제를 더 작은 하위 문제로 나누고, 하위 문제를 재귀적으로 해결한 후, 그 결과를 결합하여 원래 문제를 해결합니다. 분할 정복을 사용하면 실행 시간을 쉽게 분석할 수 있으며, 삽입 정렬보다 훨씬 빠른 정렬 알고리즘을 설계할 수 있습니다.

2.3.1 분할 정복 방법

분할 정복 방법은 다음과 같은 세 단계로 이루어집니다:
1. 분할(Divide): 문제를 더 작은 하위 문제로 나눕니다.
2. 정복(Conquer): 하위 문제를 재귀적으로 해결합니다.
3. 결합(Combine): 하위 문제의 해결책을 결합하여 원래 문제를 해결합니다.

병합 정렬(merge sort)은 분할 정복 방법을 따르는 대표적인 알고리즘입니다. 이 알고리즘은 배열을 반으로 나누고, 각각을 재귀적으로 정렬한 후, 정렬된 두 부분을 병합합니다. 재귀는 부분 배열의 크기가 1이 되면 종료됩니다.

이제 이 내용을 바탕으로 문제를 해결하고 코드를 작성할 수 있습니다. 추가 질문이 있다면 언제든지 물어보세요! 😊

분할 정복(Divide-and-Conquer)과 병합 정렬(Merge Sort)

많은 유용한 알고리즘은 재귀적 구조(recursive structure)를 가지고 있습니다. 이들은 주어진 문제를 해결하기 위해 자신을 한 번 이상 호출하여 관련된 하위 문제를 처리합니다. 이러한 알고리즘은 일반적으로 분할 정복(divide-and-conquer) 방법을 따릅니다. 분할 정복은 문제를 더 작은 하위 문제로 나누고, 하위 문제를 재귀적으로 해결한 후, 그 해결책을 결합하여 원래 문제의 해결책을 만드는 방식입니다.

분할 정복의 세 단계

분할(Divide):
문제를 더 작은 하위 문제로 나눕니다. 하위 문제는 원래 문제와 유사하지만 크기가 더 작습니다.
정복(Conquer):
하위 문제를 재귀적으로 해결합니다. 하위 문제가 충분히 작다면(기본 사례, base case), 직접 해결합니다.
결합(Combine):
하위 문제의 해결책을 결합하여 원래 문제의 해결책을 만듭니다.

병합 정렬(Merge Sort)

병합 정렬은 분할 정복 방법을 따르는 대표적인 알고리즘입니다. 병합 정렬은 배열을 반으로 나누고, 각각을 재귀적으로 정렬한 후, 정렬된 두 부분을 병합하여 전체 배열을 정렬합니다.

병합 정렬의 동작 방식

분할(Divide):
정렬할 배열 ( A[p : r] )을 두 개의 하위 배열로 나눕니다. 중간 지점 ( q )를 계산하여 ( A[p : q] )와 ( A[q+1 : r] )로 나눕니다.
정복(Conquer):
각 하위 배열 ( A[p : q] )와 ( A[q+1 : r] )을 재귀적으로 정렬합니다.
결합(Combine):
정렬된 두 하위 배열을 병합하여 하나의 정렬된 배열로 만듭니다.

기본 사례(Base Case)

재귀는 하위 배열의 크기가 1이 되면 종료됩니다. 크기가 1인 배열은 이미 정렬된 상태이므로 추가 작업이 필요하지 않습니다.

병합(Merge) 연산

병합 정렬의 핵심 연산은 병합(merge) 단계입니다. 이 단계에서는 두 개의 정렬된 하위 배열을 하나의 정렬된 배열로 합칩니다.

병합 과정

두 개의 정렬된 하위 배열 ( A[p : q] )와 ( A[q+1 : r] )을 임시 배열 ( L )과 ( R )에 복사합니다.
( L )과 ( R )의 가장 작은 요소를 비교하여 원래 배열 ( A[p : r] )에 차례대로 배치합니다.
( L ) 또는 ( R ) 중 하나가 먼저 소진되면, 나머지 배열의 요소를 ( A[p : r] )에 그대로 복사합니다.

병합의 시간 복잡도

병합 연산은 두 하위 배열의 크기를 합한 ( n )에 비례하는 시간이 걸립니다. 따라서 병합의 시간 복잡도는 ( \Theta(n) )입니다.

병합 정렬의 의사코드

MERGE-SORT(A, p, r):
    if p < r:
        q = floor((p + r) / 2)  # 중간 지점 계산
        MERGE-SORT(A, p, q)     # 왼쪽 하위 배열 정렬
        MERGE-SORT(A, q+1, r)   # 오른쪽 하위 배열 정렬
        MERGE(A, p, q, r)       # 두 하위 배열 병합

MERGE(A, p, q, r):
    nL = q - p + 1  # 왼쪽 하위 배열의 길이
    nR = r - q      # 오른쪽 하위 배열의 길이
    let L[0 : nL-1] and R[0 : nR-1] be new arrays

    # 왼쪽 하위 배열 복사
    for i = 0 to nL-1:
        L[i] = A[p + i]

    # 오른쪽 하위 배열 복사
    for j = 0 to nR-1:
        R[j] = A[q + j + 1]

    i = 0  # L의 인덱스
    j = 0  # R의 인덱스
    k = p  # A의 인덱스

    # L과 R의 요소를 비교하여 A에 병합
    while i < nL and j < nR:
        if L[i] ≤ R[j]:
            A[k] = L[i]
            i = i + 1
        else:
            A[k] = R[j]
            j = j + 1
        k = k + 1

    # L에 남은 요소를 A에 복사
    while i < nL:
        A[k] = L[i]
        i = i + 1
        k = k + 1

    # R에 남은 요소를 A에 복사
    while j < nR:
        A[k] = R[j]
        j = j + 1
        k = k + 1

병합 정렬의 시간 복잡도

분할(Divide): 배열을 반으로 나누는 데 ( O(1) ) 시간이 걸립니다.
정복(Conquer): 두 개의 하위 문제를 재귀적으로 해결합니다. 각 하위 문제의 크기는 ( n/2 )입니다.
결합(Combine): 두 하위 배열을 병합하는 데 ( \Theta(n) ) 시간이 걸립니다.

전체 시간 복잡도는 다음과 같습니다:
[
T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n)
]
이 재귀식을 풀면 ( T(n) = \Theta(n \log n) )이 됩니다.

병합 정렬의 장점

안정적(Stable): 동일한 값의 요소들이 정렬 후에도 원래 순서를 유지합니다.
일관된 성능: 최악의 경우와 평균적인 경우 모두 ( \Theta(n \log n) )의 시간 복잡도를 가집니다.

예시

입력 배열: ( A = [38, 27, 43, 3, 9, 82, 10] )

분할:
- ( [38, 27, 43, 3] )과 ( [9, 82, 10] )으로 나눕니다.
정복:
- ( [38, 27, 43, 3] )을 ( [27, 38] )과 ( [3, 43] )으로 나누고 병합합니다.
- ( [9, 82, 10] )을 ( [9] )와 ( [10, 82] )으로 나누고 병합합니다.
결합:
- ( [3, 27, 38, 43] )과 ( [9, 10, 82] )을 병합하여 ( [3, 9, 10, 27, 38, 43, 82] )를 얻습니다.

이제 병합 정렬의 동작 원리와 시간 복잡도를 이해하셨을 것입니다. 추가 질문이 있다면 언제든지 물어보세요! 😊

문제 2.3-1: 병합 정렬(Merge Sort)의 동작 예시

배열 ( \langle 3, 41, 52, 26, 38, 57, 9, 49 \rangle )에 대해 병합 정렬을 수행하는 과정을 설명하겠습니다.

과정

초기 배열:
( [3, 41, 52, 26, 38, 57, 9, 49] )
분할(Divide):
- 배열을 반으로 나눕니다:
  ( [3, 41, 52, 26] )과 ( [38, 57, 9, 49] ).
재귀적 정렬(Conquer):
- ( [3, 41, 52, 26] )을 다시 나눕니다:
  ( [3, 41] )과 ( [52, 26] ).
- ( [3, 41] )은 이미 정렬되어 있습니다.
- ( [52, 26] )을 정렬합니다: ( [26, 52] ).
- ( [3, 41] )과 ( [26, 52] )를 병합합니다: ( [3, 26, 41, 52] ).
- ( [38, 57, 9, 49] )을 다시 나눕니다:
  ( [38, 57] )과 ( [9, 49] ).
- ( [38, 57] )은 이미 정렬되어 있습니다.
- ( [9, 49] )은 이미 정렬되어 있습니다.
- ( [38, 57] )과 ( [9, 49] )를 병합합니다: ( [9, 38, 49, 57] ).
병합(Combine):
- ( [3, 26, 41, 52] )과 ( [9, 38, 49, 57] )를 병합합니다:
  ( [3, 9, 26, 38, 41, 49, 52, 57] ).

결과

최종 정렬된 배열:
( [3, 9, 26, 38, 41, 49, 52, 57] )

문제 2.3-2: MERGE-SORT의 조건

MERGE-SORT의 1번 줄에서 if p ≥ r 대신 if p ≠ r을 사용해도 되는지 설명하겠습니다.

초기 호출:
MERGE-SORT(A, 1, n)에서 ( n \geq 1 )이면, 모든 재귀 호출에서 ( p \leq r )이 보장됩니다.
재귀 호출:
중간 지점 ( q )는 항상 ( p \leq q < r )을 만족하므로, ( p > r )인 경우는 발생하지 않습니다.

따라서 if p ≠ r을 사용해도 문제가 없습니다.

문제 2.3-3: MERGE의 루프 불변식

MERGE 프로시저의 12–18번 줄의 while 루프에 대한 루프 불변식을 설명하겠습니다.

루프 불변식:

( A[p : k-1] )은 ( L[0 : i-1] )과 ( R[0 : j-1] )의 모든 요소를 포함하며 정렬되어 있습니다.
( L[i] )와 ( R[j] )는 ( A[k : r] )에 아직 복사되지 않은 가장 작은 요소입니다.

증명:

초기화:
( k = p ), ( i = 0 ), ( j = 0 )일 때, ( A[p : k-1] )은 비어 있으며, 루프 불변식이 성립합니다.
유지:
각 반복에서 ( L[i] )와 ( R[j] ) 중 더 작은 요소를 ( A[k] )에 복사하고, ( i ) 또는 ( j )를 증가시킵니다. 이로 인해 루프 불변식이 유지됩니다.
종료:
루프가 종료되면, ( L ) 또는 ( R ) 중 하나가 완전히 복사되었습니다. 나머지 배열의 요소를 ( A )에 복사하면 전체 배열이 정렬됩니다.

문제 2.3-4: 수학적 귀납법을 사용한 증명

( n \geq 2 )이고 ( n )이 2의 거듭제곱일 때, 재귀식 ( T(n) = 2T(n/2) + n )의 해가 ( T(n) = n \lg n )임을 증명하겠습니다.

기본 사례(Base Case):

( n = 2 )일 때, ( T(2) = 2T(1) + 2 = 2 \times 1 + 2 = 4 ).
( n \lg n = 2 \times 1 = 2 ).
(여기서 ( T(1) = 1 )로 가정)

귀납 가정(Inductive Hypothesis):

( n = k )일 때, ( T(k) = k \lg k )가 성립한다고 가정합니다.

귀납 단계(Inductive Step):

( n = 2k )일 때,
( T(2k) = 2T(k) + 2k = 2(k \lg k) + 2k = 2k(\lg k + 1) = 2k \lg (2k) ).
따라서 ( T(n) = n \lg n )이 성립합니다.

문제 2.3-5: 재귀적 삽입 정렬

재귀적 삽입 정렬의 의사코드와 최악의 경우 실행 시간을 설명하겠습니다.

의사코드:

RECURSIVE-INSERTION-SORT(A, n):
    if n > 1:
        RECURSIVE-INSERTION-SORT(A, n-1)  # A[1 : n-1]을 정렬
        INSERT(A, n)  # A[n]을 정렬된 A[1 : n-1]에 삽입

INSERT(A, n):
    key = A[n]
    i = n - 1
    while i > 0 and A[i] > key:
        A[i+1] = A[i]
        i = i - 1
    A[i+1] = key

최악의 경우 실행 시간:

재귀식: ( T(n) = T(n-1) + \Theta(n) ).
해: ( T(n) = \Theta(n^2) ).

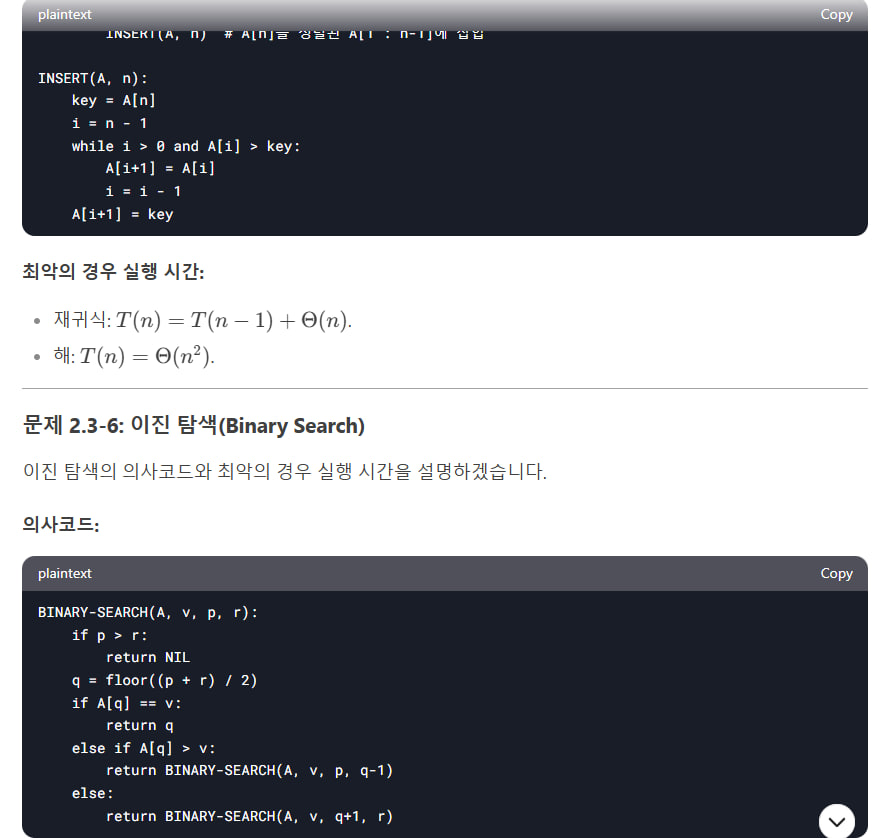
문제 2.3-6: 이진 탐색(Binary Search)

이진 탐색의 의사코드와 최악의 경우 실행 시간을 설명하겠습니다.

의사코드:

BINARY-SEARCH(A, v, p, r):
    if p > r:
        return NIL
    q = floor((p + r) / 2)
    if A[q] == v:
        return q
    else if A[q] > v:
        return BINARY-SEARCH(A, v, p, q-1)
    else:
        return BINARY-SEARCH(A, v, q+1, r)

최악의 경우 실행 시간:

( T(n) = T(n/2) + \Theta(1) ).
해: ( T(n) = \Theta(\lg n) ).

문제 2.3-7: 삽입 정렬과 이진 탐색

삽입 정렬에서 선형 탐색 대신 이진 탐색을 사용하면 최악의 경우 실행 시간이 ( \Theta(n \lg n) )이 될까요?

답:
삽입 정렬의 각 삽입 연산은 ( \Theta(n) ) 시간이 걸립니다. 이진 탐색을 사용하면 삽입 위치를 찾는 데 ( \Theta(\lg n) ) 시간이 걸리지만, 요소를 이동시키는 데 ( \Theta(n) ) 시간이 걸립니다. 따라서 전체 실행 시간은 여전히 ( \Theta(n^2) )입니다.

문제 2.3-8: 두 요소의 합

집합 ( S )와 정수 ( x )가 주어졌을 때, ( S )에서 두 요소의 합이 ( x )가 되는지 확인하는 알고리즘을 설명하겠습니다.

알고리즘:

( S )를 정렬합니다 (( \Theta(n \lg n) )).
두 포인터를 사용하여 ( S )의 시작과 끝에서 탐색합니다:
- 합이 ( x )보다 작으면 시작 포인터를 오른쪽으로 이동합니다.
- 합이 ( x )보다 크면 끝 포인터를 왼쪽으로 이동합니다.
- 합이 ( x )이면 True를 반환합니다.
탐색이 종료되면 False를 반환합니다.

시간 복잡도:

정렬: ( \Theta(n \lg n) ).
탐색: ( \Theta(n) ).
전체: ( \Theta(n \lg n) ).

문제 2-1: 병합 정렬(Merge Sort)에서 작은 배열에 삽입 정렬(Insertion Sort) 사용

a. 삽입 정렬로 ( n/k )개의 하위 리스트를 정렬하는 시간

각 하위 리스트의 크기는 ( k )입니다.
삽입 정렬의 시간 복잡도는 ( \Theta(k^2) )입니다.
( n/k )개의 하위 리스트를 정렬하는 총 시간:
(
\frac{n}{k} \times \Theta(k^2) = \Theta(nk)
).

b. 하위 리스트를 병합하는 시간

병합 정렬의 병합 단계는 ( \Theta(n \log m) ) 시간이 걸립니다. 여기서 ( m )은 병합할 리스트의 수입니다.
( n/k )개의 하위 리스트를 병합하는 시간:
(
\Theta\left(n \log \left(\frac{n}{k}\right)\right)
).

c. ( k )의 최대값

수정된 알고리즘의 총 시간 복잡도:
(
\Theta(nk + n \log(n/k))
).
표준 병합 정렬의 시간 복잡도는 ( \Theta(n \log n) )입니다.
두 알고리즘이 동일한 실행 시간을 가지려면:
(
nk + n \log(n/k) = \Theta(n \log n)
).
( k = \Theta(\log n) )일 때, ( nk = n \log n )이고 ( n \log(n/k) = n \log n - n \log k = \Theta(n \log n) ).

d. 실제로 ( k )를 선택하는 방법

( k )는 삽입 정렬이 병합 정렬보다 빠른 작은 크기로 선택합니다. 일반적으로 ( k \approx 10 \sim 20 ) 정도로 실험적으로 결정합니다.

문제 2-2: 버블 정렬(Bubble Sort)의 정확성

a. 버블 정렬이 정렬한다는 것을 증명하기 위해 필요한 것

버블 정렬이 배열을 정렬한다는 것을 증명하려면:
1. 루프 불변식(Loop Invariant): 각 외부 루프 반복 후, 배열의 마지막 ( i )개 요소는 정렬된 상태입니다.
2. 종료 조건: 모든 반복이 완료되면 전체 배열이 정렬됩니다.

b. 내부 루프(2–4번 줄)의 루프 불변식

루프 불변식:
각 내부 루프 반복 후, ( A[j] )는 ( A[j : n] )에서 가장 작은 요소입니다.
증명:
1. 초기화: ( j = n )일 때, ( A[j] )는 ( A[n : n] )의 유일한 요소이므로 루프 불변식이 성립합니다.
2. 유지: ( A[j] )와 ( A[j-1] )을 비교하여 더 작은 값을 ( A[j-1] )에 위치시킵니다. 따라서 ( A[j-1] )은 ( A[j-1 : n] )에서 가장 작은 요소가 됩니다.
3. 종료: ( j = i+1 )일 때, ( A[i+1] )은 ( A[i+1 : n] )에서 가장 작은 요소입니다.

c. 외부 루프(1–4번 줄)의 루프 불변식

루프 불변식:
각 외부 루프 반복 후, ( A[1 : i] )는 정렬된 상태이며, ( A[i+1 : n] )은 ( A[1 : i] )보다 큰 요소들로 구성됩니다.
증명:
1. 초기화: ( i = 1 )일 때, ( A[1] )은 정렬된 상태입니다.
2. 유지: 내부 루프가 ( A[i+1 : n] )에서 가장 작은 요소를 ( A[i+1] )에 위치시키므로, ( A[1 : i+1] )은 정렬된 상태가 됩니다.
3. 종료: ( i = n-1 )일 때, ( A[1 : n-1] )은 정렬된 상태이며, ( A[n] )은 가장 큰 요소입니다.

d. 버블 정렬의 최악의 경우 실행 시간

버블 정렬의 최악의 경우 실행 시간:
(
\Theta(n^2)
).
삽입 정렬과 동일한 ( \Theta(n^2) )이지만, 실제로는 삽입 정렬이 더 빠릅니다.

문제 2-3: 호너의 규칙(Horner’s Rule)

a. 호너의 규칙의 실행 시간

호너의 규칙은 ( \Theta(n) ) 시간이 걸립니다.

b. 단순한 다항식 계산 알고리즘

의사코드:

NAIVE-POLYNOMIAL-EVAL(A, n, x):
    p = 0
    for i = 0 to n:
        term = A[i]
        for j = 1 to i:
            term = term * x
        p = p + term
    return p

실행 시간:
(
\Theta(n^2)
).
호너의 규칙과 비교:
호너의 규칙은 ( \Theta(n) )이므로 훨씬 효율적입니다.

c. 호너의 규칙의 루프 불변식

루프 불변식:
각 반복 시작 시, ( p )는 ( \sum_{k=0}^{n-i-1} A[k+i+1] x^k )입니다.
증명:
1. 초기화: ( i = n )일 때, ( p = 0 )이며, 루프 불변식이 성립합니다.
2. 유지: 각 반복에서 ( p = A[i] + x \cdot p )로 업데이트되면, 루프 불변식이 유지됩니다.
3. 종료: ( i = -1 )일 때, ( p )는 ( \sum_{k=0}^n A[k] x^k )입니다.

문제 2-4: 역순(Inversions)

a. 배열 ( \langle 2, 3, 8, 6, 1 \rangle )의 역순

역순: ( (2,1), (3,1), (8,6), (8,1), (6,1) ).

b. 가장 많은 역순을 가진 배열

배열이 완전히 역순일 때 가장 많은 역순을 가집니다.
예: ( \langle n, n-1, \dots, 1 \rangle ).
역순의 수:
(
\frac{n(n-1)}{2}
).

c. 삽입 정렬의 실행 시간과 역순의 관계

삽입 정렬의 실행 시간은 역순의 수에 비례합니다.
각 역순은 삽입 정렬에서 한 번의 비교 및 교환을 필요로 합니다.
따라서 실행 시간은 ( \Theta(n + d) ), 여기서 ( d )는 역순의 수입니다.

d. 역순의 수를 계산하는 알고리즘

알고리즘:
병합 정렬을 수정하여 역순의 수를 계산합니다.
병합 과정에서 왼쪽 하위 배열의 요소가 오른쪽 하위 배열의 요소보다 큰 경우 역순으로 간주합니다.
시간 복잡도:
(
\Theta(n \log n)
).

이제 모든 문제를 해결했습니다. 추가 질문이 있다면 언제든지 물어보세요! 😊

재귀식 ( T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n) )을 풀어서 ( T(n) = \Theta(n \log n) )이 되는 과정을 상세히 설명하겠습니다. 이 재귀식은 병합 정렬(Merge Sort)과 같은 분할 정복 알고리즘에서 자주 등장합니다.

1. 재귀 트리(Recursion Tree) 방법

재귀 트리를 사용하여 재귀식을 풀어보겠습니다.

재귀 트리 구성

루트 노드:
( T(n) )은 ( \Theta(n) )의 비용을 가지며, 두 개의 하위 문제 ( T\left(\frac{n}{2}\right) )로 분할됩니다.
첫 번째 레벨:
두 개의 하위 문제 ( T\left(\frac{n}{2}\right) ) 각각은 ( \Theta\left(\frac{n}{2}\right) )의 비용을 가지며, 다시 두 개의 하위 문제 ( T\left(\frac{n}{4}\right) )로 분할됩니다.
두 번째 레벨:
네 개의 하위 문제 ( T\left(\frac{n}{4}\right) ) 각각은 ( \Theta\left(\frac{n}{4}\right) )의 비용을 가집니다.
이 과정을 반복:
재귀 트리의 각 레벨에서 비용은 ( \Theta(n) )입니다.
트리의 깊이는 ( \log_2 n )입니다.

총 비용 계산

각 레벨의 비용: ( \Theta(n) ).
레벨의 수: ( \log_2 n ).
따라서 총 비용:
(
T(n) = \Theta(n) \times \log_2 n = \Theta(n \log n)
).

2. 마스터 정리(Master Theorem) 적용

마스터 정리를 사용하여 재귀식을 풀 수도 있습니다. 마스터 정리는 다음과 같은 형태의 재귀식에 적용됩니다:
[
T(n) = aT\left(\frac{n}{b}\right) + f(n)
]
여기서 ( a \geq 1 ), ( b > 1 ), 그리고 ( f(n) )은 점근적으로 양의 함수입니다.

마스터 정리 적용

주어진 재귀식:
[
T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n)
]
여기서:

( a = 2 ),
( b = 2 ),
( f(n) = \Theta(n) ).

마스터 정리의 세 가지 경우 중에서:
1. ( f(n) = O(n^{\log_b a - \epsilon}) ) for some ( \epsilon > 0 ):
( T(n) = \Theta(n^{\log_b a}) ).

( f(n) = \Theta(n^{\log_b a}) ):
( T(n) = \Theta(n^{\log_b a} \log n) ).
( f(n) = \Omega(n^{\log_b a + \epsilon}) ) for some ( \epsilon > 0 ), and ( af\left(\frac{n}{b}\right) \leq cf(n) ) for some ( c < 1 ):
( T(n) = \Theta(f(n)) ).

주어진 재귀식에서:

( \log_b a = \log_2 2 = 1 ),
( f(n) = \Theta(n) = \Theta(n^{\log_b a}) ).

따라서 두 번째 경우에 해당하며, 해는:
[
T(n) = \Theta(n^{\log_b a} \log n) = \Theta(n \log n)
]

3. 수학적 귀납법(Mathematical Induction)

수학적 귀납법을 사용하여 ( T(n) = \Theta(n \log n) )임을 증명할 수도 있습니다.

기본 사례(Base Case):

( n = 1 )일 때, ( T(1) = \Theta(1) ).
( n \log n = 1 \times 0 = 0 ).
(여기서 ( T(1) = \Theta(1) )로 가정)

귀납 가정(Inductive Hypothesis):

( n = k )일 때, ( T(k) = \Theta(k \log k) )가 성립한다고 가정합니다.

귀납 단계(Inductive Step):

( n = 2k )일 때,
(
T(2k) = 2T(k) + \Theta(2k) = 2 \times \Theta(k \log k) + \Theta(2k) = \Theta(2k \log k + 2k)
).
- ( \log k = \log(2k) - 1 )이므로,
  (
  T(2k) = \Theta(2k (\log(2k) - 1) + 2k) = \Theta(2k \log(2k) - 2k + 2k) = \Theta(2k \log(2k))
  ).

따라서 ( T(n) = \Theta(n \log n) )이 성립합니다.

결론

재귀식 ( T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n) )의 해는 ( T(n) = \Theta(n \log n) )입니다. 이는 재귀 트리, 마스터 정리, 수학적 귀납법을 통해 모두 확인할 수 있습니다. 😊

탁가이버

더 나은 세상은 가능하다를 믿고 실천하는 활동가

이전 포스트

BeingRichardFeynman

다음 포스트

MergeSort

Algorithm

연습 문제

2.2-1

2.2-2

2.2-3

2.2-4

2.3 알고리즘 설계

2.3.1 분할 정복 방법

분할 정복(Divide-and-Conquer)과 병합 정렬(Merge Sort)

분할 정복의 세 단계

병합 정렬(Merge Sort)

병합 정렬의 동작 방식

기본 사례(Base Case)

병합(Merge) 연산

병합 과정

병합의 시간 복잡도

병합 정렬의 의사코드

병합 정렬의 시간 복잡도

병합 정렬의 장점

예시

문제 2.3-1: 병합 정렬(Merge Sort)의 동작 예시

과정

결과

문제 2.3-2: MERGE-SORT의 조건

문제 2.3-3: MERGE의 루프 불변식

루프 불변식:

증명:

문제 2.3-4: 수학적 귀납법을 사용한 증명

기본 사례(Base Case):

귀납 가정(Inductive Hypothesis):

귀납 단계(Inductive Step):

문제 2.3-5: 재귀적 삽입 정렬

의사코드:

최악의 경우 실행 시간:

문제 2.3-6: 이진 탐색(Binary Search)

의사코드:

최악의 경우 실행 시간:

문제 2.3-7: 삽입 정렬과 이진 탐색

문제 2.3-8: 두 요소의 합

알고리즘:

시간 복잡도:

문제 2-1: 병합 정렬(Merge Sort)에서 작은 배열에 삽입 정렬(Insertion Sort) 사용

a. 삽입 정렬로 ( n/k )개의 하위 리스트를 정렬하는 시간

b. 하위 리스트를 병합하는 시간

c. ( k )의 최대값

d. 실제로 ( k )를 선택하는 방법

문제 2-2: 버블 정렬(Bubble Sort)의 정확성

a. 버블 정렬이 정렬한다는 것을 증명하기 위해 필요한 것

b. 내부 루프(2–4번 줄)의 루프 불변식

c. 외부 루프(1–4번 줄)의 루프 불변식

d. 버블 정렬의 최악의 경우 실행 시간

문제 2-3: 호너의 규칙(Horner’s Rule)

a. 호너의 규칙의 실행 시간

b. 단순한 다항식 계산 알고리즘

c. 호너의 규칙의 루프 불변식

문제 2-4: 역순(Inversions)

a. 배열 ( \langle 2, 3, 8, 6, 1 \rangle )의 역순

b. 가장 많은 역순을 가진 배열

c. 삽입 정렬의 실행 시간과 역순의 관계

d. 역순의 수를 계산하는 알고리즘

1. 재귀 트리(Recursion Tree) 방법

재귀 트리 구성

총 비용 계산

2. 마스터 정리(Master Theorem) 적용

마스터 정리 적용

3. 수학적 귀납법(Mathematical Induction)

기본 사례(Base Case):

귀납 가정(Inductive Hypothesis):

귀납 단계(Inductive Step):

결론

BeingRichardFeynman

CLRS

0개의 댓글