✅ 최적화
✍️ Generalization
일반화라 불리며 일반화 성능을 향상시키기 위해선 iteration이 커질수록 error가 작아지는 train error와 재차 커지는 test error간의 차이를 뜻하는 generalization gap을 낮춰야 한다.
✍️ Cross-Validation
다른 말로, k-fold validation이라고도 한다. 구조는 아래 그림과 같다.
위 구조처럼 train data를 여러 fold로 나눈 후 한 fold를 지정해 validation을 담당하고 fold 수 만큼 train을 하며 validation fold를 변경해가며 학습하는 방법
최적의 hyperparameter를 찾은 후 이를 고정해 전체 학습 데이터에 적용하는 식으로 쓰인다.
✍️ Variance vs Bias Trade off
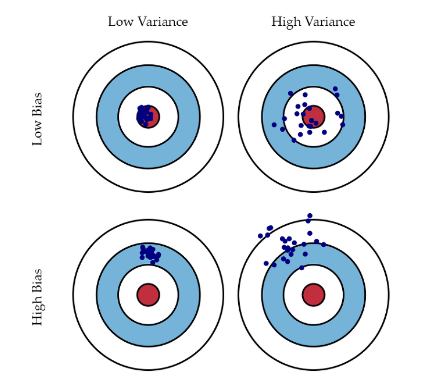
- Variance : 얼마나 Output이 일관적인가 (모여있는가)
- Bias : 얼마나 Output이 타겟에 근접한가
를 비교한 것으로 Cost = Variance + Bias + Noise 로 구성되어 있어 Noise가 존재하는 데이터에선 Variance, Bias 모두를 낮추기엔 쉽지 않다.
✍️ Boostrapping
: any test or metric that use random sampling with replacement
학습 데이터를 여러 개로 나누어 이를 각 다른 모델로 학습하는 방법
✍️ Bagging
: multiple models are being trained with boostrapping
boostrapping방식으로 여러 모델로 학습 진행함 (Parallel 느낌)
✍️ Boosting
: It focus on those specific training samples that are hard to classify
sequential한 느낌으로 A모델로 학습하다 성능이 떨어지면 다른 모델로 학습하는 방법
✅ Gradient Descent
: 최적화하는데 있어 효율을 높이는 방법으로, 딥러닝 목표인 loss function을 최소화하는 방식으로 파라미터를 찾을 때, 최적의 파라미터를 찾는 업데이트 과정을 경사를 타고 minimum값을 찾도록 하는 기법
W(t+1) = W(t) - l * g(t)
w : weight
l : learning rate
g(t) : gradient
3가지로 나뉘어서 살펴보면 다음과 같다
1. Batch Gradient Descent: 한 번에 모든 데이터셋의 slope 구하여 파라미터 업데이트
2. Mini-Batch Gradient Descent: 데이터 셋 일부에 대해서 기울기 구해 파라미터 업데이트
3. Stochastic Gradient Descent: 임의로 한 데이터의 에러를 구해 기울기 계산하여 업데이트
✍️ Momentum
Gradient Descent에서 gradient의 가중 평균치를 산출해 weight를 업데이트 하는 것으로,
모멘텀을 사용함으로써 속도가 빠르고 SGD가 overshooting, diverging 되는 것을 방지하고 local minimumu 탈출이 가능하다.
참고사항
지수 가중 평균(=지수 이동 평균)이란, 데이터의 이동 평균을 구할 때, 오래된 데이터가 미치는 영향을 지수적으로 감쇠(exponential decay) 하도록 만들어 주는 방법
수식은 다음과 같다.
W(t+1) = W(t) - l a(t)
a(t+1) = B a(t) + g(t)
a : accumulation, B : 모멘텀
위와 같은 수식으로 인해 모멘텀은 weight update 시 gradient가 바로 바뀌지 않고 방향을 유지시켜주고, 가속도 개념으로 같은 방향에는 더 많은 변화를 주어 학습 속도를 높여준다
그러나, weight 이동량 계산을 위해 momentum, gradient 2가지를 한번에 업데이트해야 한다.
✍️ NAG (Nesterov Accelerated Gradient)
: 모멘텀과 gradient step을 구한 위치가 다르고, 업데이트가 과도하게 계산되는 momentum 문제를 분할하여 개선하였다.
momentum : 지금 위치에서 gradient step을 구해서 v에 더해주면(러닝레이트를 곱하고 뺌)
NAG : 현 위치에서 관성만큼 움직인 다음의 위치에서 gradient step을 구해 v에 더해줌
코드로 구현하면 다음과 같다class Nesterov: def __init__(self, lr=0.01, momentum=0.9): self.lr = lr self.momentum = momentum self.v = None def update(self, params, grads): if self.v is None: self.v = {} for key, val in params.items(): self.v[key] = np.zeros_like(val) for key in params.keys(): self.v[key] *= self.momentum sefl.v[key] -= self.lr * grads[key] params[key] += self.momentum * self.momentum * self.v[key] params[key] -= (1 + self.momentum) * self.lr * grads[key]
✍️ Adagrad
신경망 학습에서 learning rate 값이 중요한데, 이를 효과적으로 정하기 위해 학습을 진행하며 learning rate를 decay시키는 방법으로 이를 각 매개변수에 적용시킨 것이 adagrad이다.
영향을 많이 받은 parameter일수록 적게 변화시키고, 반대의 경우엔 크게 변화시킴을 의미한다.
이를 코드로 구현하면 다음과 같다.class AdaGrad: def __init__(self, lr = 0.01): self.lr = lr self.h = None def update(self, params, grads): if self.h is None: self.h = {} for key, val in params.items(): self.h[key] = np.zeros_like(val) for key in params.keys(): self.h[key] += grads[key] * grads[key] params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)그러나, 학습 양 자체가 매우커지게 되면 학습이 줄어든다는 문제가 발생한다.
✍️ RMSProp
지수이동평균을 이용해 학습을 진행하며 이전의 오래된 학습의 기울기는 작게, 최신 기울기는 크게 반영하는 것으로 adagrad를 개선한 방법이다.
💯 Adam
RMSProp + Momentum으로 현재 가장 많이 사용하는 optimizer로 성능이 가장 좋다.
진행하던 방향의 속도에 관성을 주고, 최근 경사 변화량에 따른 adaptive learning rate를 갖추었다.
