이제 자료구조에 대한 포스트에서 다룰 주제가 크게 2가지밖에 남지 않았다. 그 중하나는 다음시간에 다룰 그래프(Graph)이고, 하나는 이번 포스트에서 다룰 테이블(Table)과 해쉬(Hash)이다.

테이블(Table)

테이블은 우리가 일상생활에서 자주보는 일종의 표라고 생각하면 편하다. 표는 저장되는 데이터를 키(key)와 값(value)이 하나의 쌍을 이루는 구조이다. 즉, 테이블도 마찬가지이다. 앞 포스트에서 다룬 AVL 트리도 굉장히 빠른 탐색 연산을 보였다. O(log2n)이라는 빠른 시간복잡도를 보였지만, 테이블은 탐색연산이 O(1)이다. 즉, 훨씬 더 빠르게 탐색할 수 있다는 특징이 있다.
테이블의 특징

• 테이블에서 키가 존재하지 않는 '값'은 저장할 수 없다.
• 모든 키는 중복될 수 없다.

그러면 배열을 기반으로 하여 테이블을 구현해보았다고 해보자. 키의 값은 저장위치(배열에서의 인덱스) 라고 생각하면 쉽게 구현할 수 있을 것이다. 그리고 또한, 데이터를 저장하거나 탐색을 하는 연산이 어렵지 않을 것이다. 하지만, 우리는 한가지의 변수를 생각하지 않을 수가 없다. 범위를 인덱스의 값으로 저장하기 애매할 때가 있다. 예를 들어, 대학교의 학번을 인덱스의 값으로 학생들의 정보를 테이블에 넣는다고 가정해보자. 학번 같은 경우는 (입학년도) + (고유번호) 로 총 8자리로 구성되어있다. 다만, 이 값은 배열에서 시작점을 0으로 할 수도 없기에 문제인 것이다. 이에 필요한 것이 해쉬함수이다.

---

해쉬(Hash)

해쉬함수(Hash Function)이란?
: 넓은 범위의 키를 좁은 범위의 키로 변경하는 역할을 하는 함수

위에 있는 학번으로 예시를 들어보자. 총 2개 20210001, 20210051이 있다. 우리는 이 두 개의 학번에 '%100'연산을 했다고 가정해보면 각각 01, 51 로 변경한 것을 확인할 수 있다. 다만, 20210151 같은 경우는 똑같은 연산을 하면 51로 겹칠 수 있을 것이다. 이러한 현상을 '충돌' 이라고 한다.

충돌이란?
: 서로 다른 키가 해쉬 함수 연산 이후 같은 값을 가지는 상황

사실 이 충돌은 해쉬함수를 사용하면 생기는 문제라고 인식 할 것이 아니라 꼭 해결을 해줘야하는 문제이다. 뒷부분에 이를 해결하는 방법들을 몇가지 알아볼 것이다. 우선 앞의 예시에서 '%100' 연산은 괜찮았을까? 사실, 2021학년 같은 경우는 아마 대부분의 학생들이 2021년도에 입학을 하였다면 고정이 되어있을 것이다. 그렇기에 %1000 연산을 한다면 공통되지 않는 부분만 딱 분류해서 인덱스에 값을 저장할 수 있기에 %100 연산은 적합하지 않았다는 결론을 내릴 수 있다. 위 설명에서 말할 수 있듯이 좋은 해쉬함수란, 충돌을 덜 일으키고 테이블 전체 영역에 골고로 퍼져있는 상태로 만들어줄 수 있을 때를 말한다. 예시를 들면 바코드 영역을 전체 테이블, 검은색 선을 해쉬함수 이후 인덱스에 저장된 값이라고 생각한다면, 규칙적으로 보이는 바코드가 좋은 해쉬함수를 사용한 결과라고 보면 좋을 것이다.

자릿수 선택(Digit Selection)

사실 앞서 설명한 예시에 사용된 기법이다. 공통으로 겹치는 부분을 제외하고, 해쉬 값 생성에 도움을 주는 수만 뽑아서 해쉬 값을 생성하는 방법이다. 숫자가 길지만, 공통으로 연결되는 숫자가 있는 경우에 사용되는 기법이라고 생각하면 좋을 것이다.

자릿수 폴딩(Digit Folding)

종이를 접듯이 숫자를 겹치게 하여 더한 결과를 해쉬 값으로 결정하는 방법이다. 이는 밑의 사진으로 예시를 보여주도록 하겠다.

---

충돌의 해결 방법

그러면 이제 중요한 해결의 충돌 방법들을 알아보도록 하겠다.

열린 어드레싱 방법(open addressing method)

열린 어드레싱이 있으면 닫힌 어드레싱 방법도 존재할 것을 눈치 챌 것이다. 일단, 충돌이라는 상황이 발생했을 때, 충돌이 발생한 곳을 피해 다른 곳의 자리에 값을 넣는 방법을 열린 어드레싱 방법이라고 하고, 이에는 다른 곳의 자리를 어떻게 찾는지의 방법에 따라 총 3가지로 나뉠 수 있다.

선형 조사법(Linear Probing)

• 충돌이 발생했을 때, 그 옆자리가 비어있는 경우에 그 자리에 대신 저장하는 방법
• f(k) + 1, f(k) + 2 , f(k) + 3 ...
• 충돌의 횟수가 증가함에 따라 클러스터 현상이 발생할 수 있음.

클러스터현상이란?
: 특정 데이터가 집중적으로 몰리는 상태를 뜻함.

이차 조사법(Quadratic Probing)

• 선형 조사법은 n칸 옆에 데이터를 저장하였다면, 이는 클러스터 현상을 대체적으로 완화하기 위해 n^2칸 옆에 데이터를 저장하는 방법
• f(k) + 1, f(k) + 4, f(k) + 9 ...
• 슬롯안에 있는 값을 저장했다가 삭제하는 경우 DELETE라는 상태를 작성해줘야함.
  : 충돌이 발생해서 주어진 자리의 옆자리에 넣어있는 경우를 확인해야 탐색이 가능하기 때문임.
• 단) 해쉬 값이 같으면, 빈 슬롯을 차는 위치가 항상 동일할 수 밖에 없음.

이중 해쉬(Double Hash)

• 두 개의 해쉬 함수를 마련
  : 1) 키를 근거로 저장위치를 결정하기 위한 해쉬함수
  : 2) 충돌 시 몇칸 뒤를 살필지 결정하는 해쉬함수

• ex) h1(k) = k % 15 / h2(k) = 1 + (k % c)
  (단, c는 15보다 작은 소수)
  

• 클러스터 현상을 낮춘다는 통계가 존재함.

닫힌 어드레싱 방법(Closed addressing method)

열린 어드레싱 방법에서는 총 3가지를 다루면서 만약 충돌이 생기면 다른 빈자리를 찾아 넣어서 충돌을 없애는 방법을 설명하였다. 이름을 보면 알 수 있듯이 닫힌 어드레싱 방법은 정확히 정반대로, 무슨 일이 있어도(충돌을 하여도) 자신의 자리에 저장하는 방법을 말한다.

체이닝(Chaining)

• 충돌 발생시 같은 키 안에 연결리스트로 이어져있는 상태
  
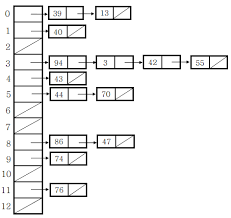
• 하나의 해쉬 값에 다수의 슬롯이 들어갈 수 있음. (나쁜 해쉬함수)
  : 해쉬함수를 잘 정의함에 따라 어느정도 해결되는 문제 ( 즉, 해쉬함수의 정의를 잘 하면 충돌이 적어지면서 좋은 테이블을 만들 수 있음.)

---

이렇게 이번에 해쉬와 테이블에 대하여 알아보았다. 테이블은 충돌을 어떻게 해결하는지의 여부만 잘 이해하고, 해쉬함수를 잘 정의하면 쉽고 효율적으로 사용할 수 있는 자료구조이다. 물론, 충돌을 해결하는 방법들을 몇가지 같이 보았지만, 제일 좋은 방법은 해쉬함수를 잘 정의하여서 충돌이 없게(바코드로 예시를 들자면, 규칙적인 바코드 모양이 나올 수 있도록) 하는 방법이 제일 좋은 방안인것이다. 그러면 다음 포스트에서 자료구조의 마지막 파트인 그래프로 오도록 하겠다.