이번 포스트에서 다룰 주제도 저번 포스트에 이어 탐색에 관한 내용이다. 하지만, 사실상 이번 포스트에도 트리에 대하여 좀 더 자세하게 공부하는 느낌으로 볼 수 있다.

AVL 트리

AVL트리에 대해 학습하기 전에, 이진탐색트리의 시간복잡도를 다시 보자. 이진탐색트리의 시간 복잡도는 O(log2n)이다. 하지만, 루트 노드를 제일 큰 수나 제일 작은수로 넣었다고 가정해보자. 그때의 트리는 사실상 배열과 가깝게 루트노드를 기준으로 왼쪽이나 오른쪽으로 쭉 뻗어있는 상황을 볼 수 있다.(그렇기에 루트노드의 값을 잘 설정해주는 것이 중요하다.) 이때는 O(n)에 가깝다.

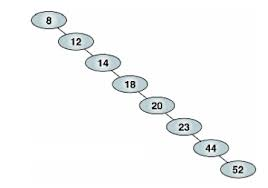
위 사진이 이에 대표적인 예시이다. 그렇기에 이진탐색트리는 정말 좋은 탐색 자료구조임에 불구하고, 저장 순서에 따라 탐색의 성능에 큰 차이를 보인다는 단점이 있다. 그렇기에 등장한 것이 이 AVL트리이다.

AVL 트리란?

• 노드가 추가될 때, 삭제될 때 트리의 균형상태를 파악해 스스로 구조를 변경하는 트리

균형 상태를 어떻게 알 것인가? '균형인수'를 사용하면 된다. 균형 인수란 루트 노드를 기준으로 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값이다. 그렇기에 이를 노드 추가/삭제 시 계산해주어 스스로 구조를 변형하면 되는 것이다. 기준은 대게로 균형인수의 절댓값이 2이상인 경우에 한다고 한다. 그러면, 총 4가지의 회전에 대해 알아보고 이번 포스트를 마무리 해보도록 하겠다.

LL 회전

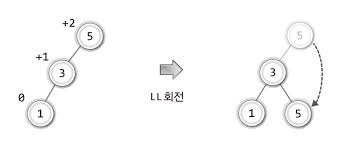
LL회전은 다음 사진과 같다. 자식 노드 2개가 왼쪽으로 연이어 연결되어 균형인수가 +2 인 상태일때 해야하는 회전을 LL회전이라고 한다. 지금부터 설명하는 모든 회전중에 부모노드를 pnode, 중간 기준이 되는 노드를 cnode라고 지칭하고 설명하겠다. 이 LL회전에서는 중간을 cnode라고 가정할 때, pnode를 cnode의 오른쪽 서브트리로 변경하면 된다. 하지만 고려해줘야하는 상황이 하나 있다. 사실, 저건 연이어 있기만 한 상황이고 원래 기존에 3에서의 오른쪽 서브트리가 존재할 수도 있다. 그때의 오른쪽 서브트리는 LL회전을 한 이후, pnode의 왼쪽 서브트리로 이동하면 된다. 즉, 그림에서 LL 회전이후 한 그림의 5의 왼쪽 서브트리에 들어가게 되는 것이다.

RR 회전

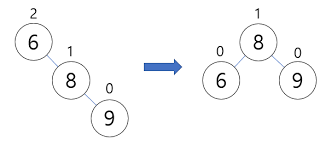
RR회전은 다음 사진과 같다. 이름과 같게 LL회전의 정반대라고 생각하면 된다. RR회전은 자식 노드 2개가 오른쪽으로 연이어 연결되어 균형인수가 -2인 상태일 떄 하는 회전이다. pnode를 cnode의 왼쪽 자식 노드가 되게 하여, cnode의 왼쪽 서브트리를 pnode의 오른쪽 서브트리가 되게 하면 된다. LL회전과 반대되는 방향으로 같은 설명이기에 이정도만 하고 넘어가도록 하겠다.

LR 회전과 RL 회전

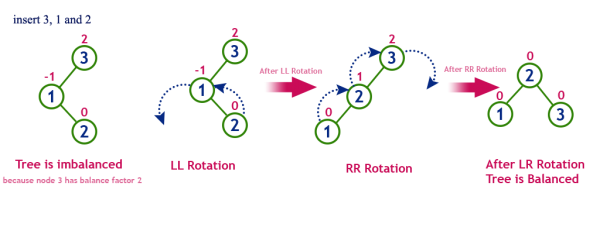
LR회전과 RL 회전도 사실 정반대의 설명이여서 이번에는 하나로 묶어서 설명해보겠다. LR회전은 똑같이 자식 노드가 연달아 있는 상황에 쓰이는 회전이다. 다만, 1개는 L, 그 다음 노드는 R에 위치한 상태를 말한다. 이때는 LR 회전을 해주어야하고, 만약 반대되는 상황에 있을 때는 RL 회전을 사용하면 된다. LR 회전의 그림을 보자. 1,2,3 이라는 총 노드 3개가 LR회전이 필요한 상태에 놓여져있다. 우선, 1과 2를 RR 회전을 먼저 해준다. RR회전은 두개의 노드로만 진행해도 된다. 그 이유는 2의 오른쪽 서브트리에 공집합 노드가 있다고 가정하고 계산해도 되기 때문이다. 그렇게 하면 1은 2의 왼쪽 서브트리에 있게 될 것이다. 사실상 그러면, 우리는 LL 회전을 해야만 했던 상황으로 오게 된 것이다. 따라서 LR 상태를 RR회전을 통해서 LL로 변경한 이후에 LL회전을 하여 정리하는 것이 LR 회전, 그 반대되는 상황에서는 RL 회전이라고 한다.