물론 이 포스트의 제목은 탐색이다. 하지만, 관련 범위를 학습하다보면, 이는 앞서 정렬의 방법들을 열거한 것과는 다르게 트리의 심화학습과 같다는 생각이 들었다. 사실상, 트리라는 자료구조를 우리가 더 효율적인 탐색 방법을 위한 저장 방법이라고 생각하면 더 편하게 생각할 수 있을 것 같다.
보간 탐색(Interpolation Search)
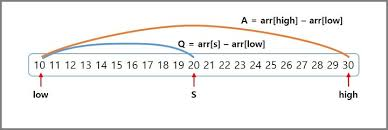
위 사진이 바로 보간 탐색의 기본 구성도이다.
보간 탐색이란?
- 이진 탐색을 더 효율적으로 변경한 탐색으로 무작정 중앙에서 탐색하지 않고, 탐색 대상의 위치와 비례하게 탐색하는 탐색
대상의 위치와 비례한다는 말은 상대적으로 앞이면 앞, 뒤면 뒤라고 생각하고 넘어가면 좋을 것 같다. 위 그림을 통해서 식을 정리해보겠다.
A : arr[high] - arr[low] (자료의 전체 길이)
Q : arr[s] - arr[low] (찾으려고 하는 데이터부터 초반까지의 길이)
A : Q = (high - low) : (s - low)
사실 위 두 개의 식을 마지막 식에 대입해서 s에 대하여 식을 정리하면 된다.
s = ((x - arr[low]) / (arr[high] - arr[low])) * (high - low) + low
로 정리할 수 있다. 이때 이를 코드에 대입할 때는 double 형, 즉 실수형 나눗셈으로 계산을 해야 오차율을 더 줄일 수 있다.
- 여기서 잠깐?
탐색키 (Search Key) 와 탐색 데이터 (Search Data)
: 배열에서 ~~을 찾는다 ( 탐색 데이터 )
: 배열에서 ~번째를 찾는다. (탐색 키)
-> 즉 탐색키는 고유해야한다는 성질이 존재함.
보간탐색의 구현
구현 과정은 사실 크게 더 배울 것은 없다. 위의 비례식 식을 원래 이진 탐색을 하는 알고리즘을 가져와서 약간만 수정해주면 된다. 원래 mid라는 가운데를 기준으로 우리가 찾는 target데이터가 더 큰지 작은지를 통해 재귀를 통해서 데이터를 찾았다면, 여기서는 mid를
mid = ((double)(target - arr[first]) / (arr[last] - arr[first])
* (last - first) + first;이렇게 된다.
탈출조건은 원래 이진 탐색 트리에서는 first가 last보다 큰 경우일 때이지만, 이 보간탐색을 할 때에는 탐색대상이 존재하지 않는 경우, 재귀적 함수의 호출로 target이 값의 범위를 벗어날 수 있기에 이 부분을 탈출조건으로 제시해주어야 한다.
arr[first] > target || arr[last] < target이진탐색트리
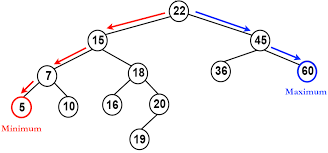
이진탐색트리에서는 딱 4가지의 특징만 알고가면 된다.
- 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
- 루트노드의 키가 왼쪽 서브트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트노드의 키가 오른쪽 서브트리를 구성하는 어떠한 노드의 키보다 작다.
- 루트노드를 기준으로 왼쪽과 오른쪽 서브트리도 이진 탐색트리이다. 그 이후도 마찬가지이다.
이진탐색트리의 구현
위 4가지의 특징만 잘 암기하고 있으면 된다. 그러면 밑에 있는 구현도 개념은 쉽게 이해할 수 있다. 구현하는 과정은 직접 연습해보는 것이 좋을 것이다.
1) 삽입 , 탐색
- 비교 대상이 없을 때까지 (While문 사용) 내려간다. 비교대상이 없는 그 위치가 즉 새 데이터를 저장하는 위치 이다.
2) 삭제
삭제 시에는 총 3가지의 경우를 나눠서 계산해야한다. if ~ else문을 사용하여 3가지 경우를 다루어 이를 하나의 함수안에 작성해주어야한다. 다음은 그 3가지의 경우이다.
-
상황 1 : 삭제할 노드가 단말경우인 경우
: 삭제할 노드까지 탐색한 이후에 삭제한다. 제일 간단하고, 삽입 탐색처럼 위치를 찾고 반환 후 삭제하기만 하면된다. -
상황 2 : 삭제할 노드가 하나의 자식 노드
: if - else문을 활용해 노드의 부모노드와 자식노드를 연결한다. 이렇게 하는 이유는 자식노드가 다른 노드의 부모노드가 될 수 있기에 자식 노드를 지우게 되버리면 자식노드의 자식노드의 값이 이진탐색트리에 연결이 끊기기 때문에 위 아래에만 연결해주는 것이 정답이다. -
상황 3 : 삭제할 노드가 2개의 자식 노드를 갖는 경우
: 이는 윗 상황의 문제도 생각하면서 접근해야한다. 사실 그림을 보면서 이해하면 좋을 것이다. 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 값이나, 오른쪽 서브트리에서 가장 작은 값을 저장하면 된다.
