Binary classification model 의 결과는 확률인가?
2
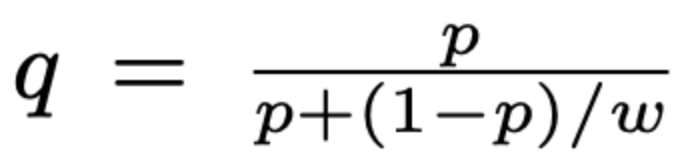
Binary Model 의 결과를 사건의 발생 확률이라고 해석해도 될까?
위 질문에 대한 정답은 그렇게 해석해도 될 때도 있고, 아닐때도 있다 라는것이다.
1. Probability Recalibration
Classification 문제에서 data 가 imbalanced 되어있을 경우, 빠른 학습을 위해 negative downsampling 을 하게 된다.
그런데, negative downsampling을 하면 prediction 값 또한 negative downsample 된 space 맞게 calibration 되는것이 당연하다.
→ 즉 real space 에 맞게 recalibration 을 해주는 과정이 필요하다!
e.g. sample 이전의 ctr 이 0.1%였다면, negative downsampling 을 0.01만큼 해줬다면 pctr은 약 10% 가 되었을 것.
이때의 recalibration 아래의 식을 통해서 한다 (q는 recalibrated probability, p 는 predicted probability, w는 sampling rate)
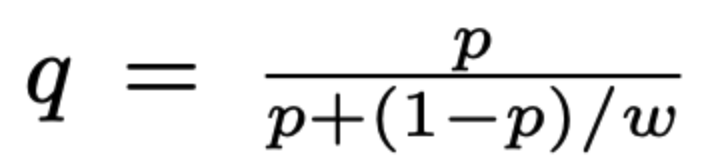
2. Recalibration 식의 유도과정
- Let original imbalanced data
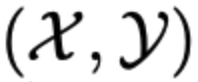
- Let sampled balanced data (x, y)
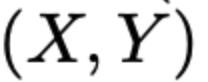
- Let s = random binary selection variable for each of N samples in original unbalanced data
- 즉, 해당 데이터가 sampling 된 데이터 (x,y)에 포함돼있다면 1, 없다면 0으로 표현된다. - sampling 을 할 때에는 x값에 상관없이 sample 할 것이므로 (independent) 아래의 식이 성립한다.
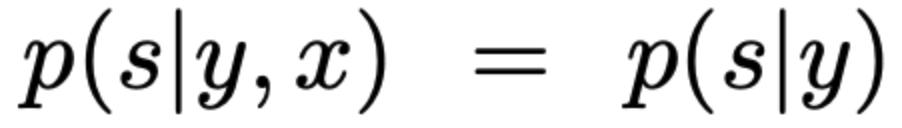
- 또한 위의 가정은 아래의 식의 의미를 내포한다.
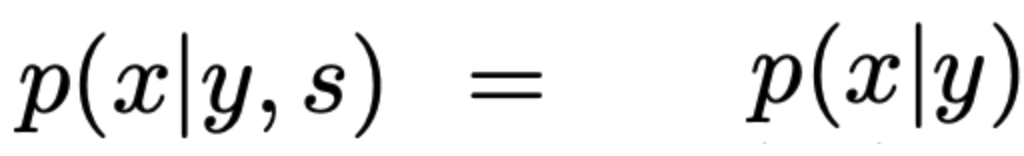
- y=1을 + 로, y=0을 -로 정의한다면, sampling 된 데이터에서 y=1인 경우에 대한 확률은 아래와 같이 표현할 수 있다.
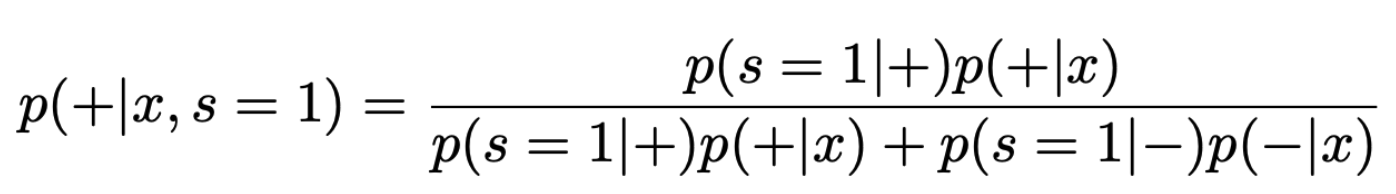
- 위의 식에 p(s=1|+)=1 original data 중 y=1인 경우라면 sample 된 데이터에 항상 들어간다)을 대입하면
- (위 내용에 설명을 보태자면, original data가 y=1인 경우가 희소하고, y=0인 경우가 압도적으로 많은 imbalanced data일 경우, negative sampling 을 하게 된다. 이 경우 sampling 된 데이터에는 y=1인 경우에 대한 데이터는 전부 들어가는 한편, y=0인 경우에 대한 데이터는 sampling 되어 들어가게 된다)
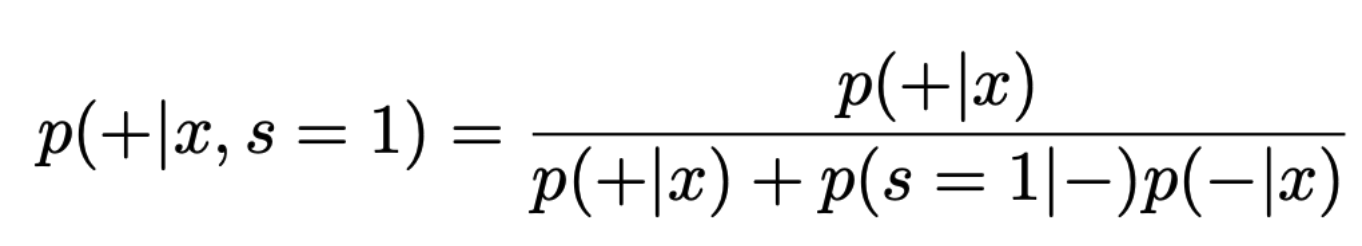
- p(s=1|-)를 beta라고 표현 / p(+|x,s=1)은 sampling 한 것들 중에 y=1일 확률 이므로 p_s로 표현한다면 위의 식은 아래처럼 표현 가능하다.
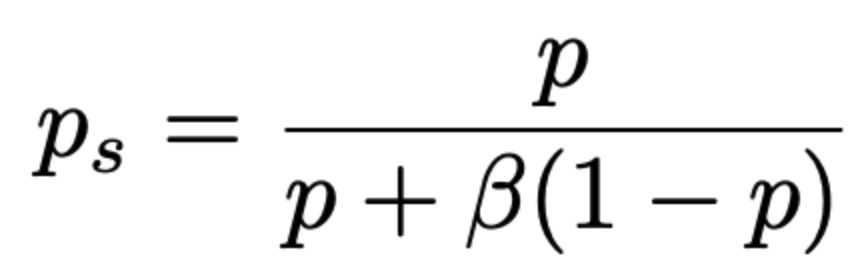
- 위의 식을 p의 식으로 정리하면
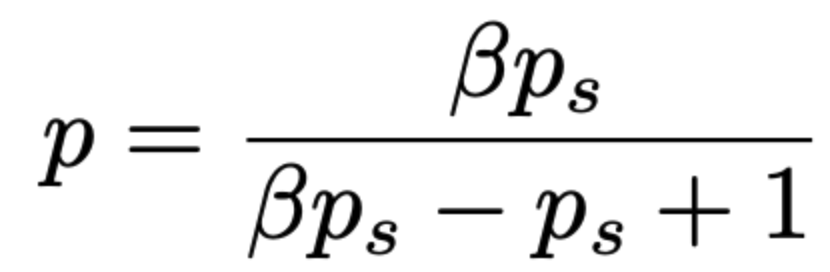
- beta 는 위에서의 정의에서, negative 한 것들 중에 sampling 된 것들, 즉 negative sampling rate 이므로 아래처럼 표현될 수 있음 (N+, N- 각각은 positive, negative instances)
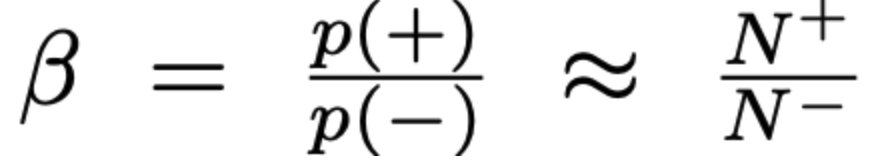
- 윗윗 불릿(ㅋㅋ)의 p의 식에서 분자, 분모를 beta로 나누고, beta 를 w로 나타내면 아래의 식이 나온다! (아래의 식에서 q는 recalibration 된 probability 를, p는 위에서의 p_s)
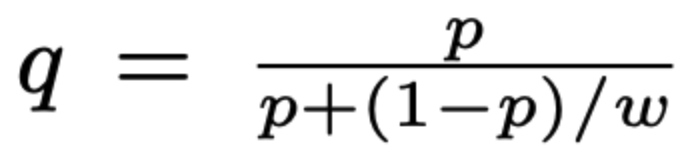
3. 참고자료
- 활용 예시 논문 : Practical Lessons from Predicting Clicks on Ads at Facebook (2014)
- 식 유도 및 결과를 분석한 논문 : Calibrating Probability with Undersampling for Unbalanced Classification (2015)
- 꼭 논문이 아니더라도 검색하면 많이나와요
- https://stats.stackexchange.com/questions/294494/convert-predicted-probabilities-after-downsampling-to-actual-probabilities-in-cl
- https://datascience.stackexchange.com/questions/58631/is-there-a-way-to-re-calibrate-predicted-probabilities-after-using-class-weights
- https://www.linkedin.com/pulse/event-rate-prediction-7-key-problems-solutions-while-using-bendale