1. 수반연산자

이전에 행렬 $A$에 대한 켤레 전치행렬 $A^*$를 정의했었다. 행렬과 연산자는 뗄레야 뗄 수 없는 관계이기 때문에, 켤레 전치행렬에 대한 연산자 역시 따로 정의되어 있다.

정의 1. $V$의 임의의 정규직교기저 $\beta$에 대한 행렬표현이 $[T]_\beta^*$인 선형연산자를 $T$의 수반연산자라 한다.

이때, 내적공간 $V$와 $y \in V$에 대하여 $g(x) = <x, y>$로 정의한 함수 $g:V \to F$는 선형일 것이다. 여기서 만약 $V$가 유한차원이라면, $V$에서 $F$로 가는 모든 선형변환은 모두 $<x, y>$와 같은 꼴일 수밖에 없게 된다.

정리 1. 유한차원 $F$-내적공간 $V$와 선형변환 $g:V\to F$를 생각하자. 모든 $x \in V$에 대하여 $g(x) = <x, y>$를 만족하는 벡터 $y \in V$가 유일하게 존재한다.

증명
$V$의 정규직교기저 $\{v_1, v_2, \dots, v_n\}$에 대하여 $y = \sum^n_{i=1}\overline{g(v_i)}v_i$라 하자. 함수 $h : V \to F$를 $h(x) = <x, y>$로 정의하면, $h$는 선형이어야 한다. 또한 $1\leq j \leq n$에 대해 다음 식이 성립한다.

즉, $g$와 $h$는 모든 $\beta$의 원소에 대해 동일한 함수값을 가지므로 동일한 선형변환이라 할 수 있다. 이때, 모든 $x$에 대해 $g(x) = <x, y'>$이라 가정하면, 모든 $<x, y> = <x, y'>$이 성립하므로, $y= y'$이고, $y$는 유일하다는 것을 알 수 있다.

이제 내적공간의 수반연산자에 대해 정리해보자.

정리 2. 유한차원 내적공간 $V$와 선형연산자 $T: V \to V$를 생각하자. 모든 $x, y \in V$에 대하여 $<T(x), y> = <x, T^*(y)>$인 함수 $T^* : V \to V$가 존재한다. 특히 $T^*$는 선형변환이다.

즉, 선형연산이 유일하게 존재하듯이, 수반연산도 유일하게 존재한다는 의미이다.
증명
$y \in V$를 고정하고, 모든 $x \in V$에 대하여 함수 $g: V \to F$를 $g(x) = <T(x), y>$로 정의해보자. 이제 1. $g$가 선형임을 보이고, 2. $T^*$이 선형임을 보이고, 3. $T^*$이 유일함을 보여 증명할 것이다.

1. $g$가 선형임을 보이자.
   $x_1, x_2 \in V$와 $c \in F$에 대하여 다음이 성립함을 알 수 있다.

   $\begin{aligned} g(cx_1 + x_2) &= <T(cx_1 + x_2), y> \\ &= <cT(x_1) + T(x_2),y> \\ &= c<T(x_1), y> + <T(x_2), y> \\ &= cg(x_1) + g(x_2) \end{aligned}$

   위와 같이 간단하게 $g$가 선형임을 알 수 있다.
   또한 정리 1에 의해 $g(x) = <x, y'>$의 유일ㄹ한 $y'$가 존재하는 것을 알고 있다. 이는 $<T(x), y> = <x, y'>$가 되고, $T^* : V\to V$를 $T^*(y) = y'$이라 정의한다면 $<T(x), y> = <x, T^*(x)>$가 성립하게 된다.

2. $T^*$가 선형임을 보이자.
   $y_1, y_2 \in V, c \in F$를 고정하면, 임의의 $x \in V$에 대하여 다음이 성립할 것이다.

   $\begin{aligned} <x, T^*(cy_1 + y_2)> &= <T(x), cy_1 + y_2)\\ &= \bar{c}<T(x), y_1> + <T(x), y_2>\\ &= \bar{c}<x, T^*(y_1)> + <x, T^*(y_2)>\\ &=<x, cT^*(y_1) + T^*(y_2)> \end{aligned}$

   여기서 $x$를 특정 벡터로 한정짓지 않았기 때문에, $T^*(cy_1 + y_2) = cT^*(y_1) + T(y_2)$가 성립하고, $T^*$가 선형임을 알 수 있다.

3. $T^*$가 유일함을 보이자.
   $U : V\to V$가 선형이고, 모든 $x, y \in V$에 대하여 $<T(x), y> = x, U(y)>$를 만족한다고 가정해보자. $x, y \in V$에 대하여 $<x, T^*(y)> = <x, U(y)>$이므로, $T^* =U$이고, $T^*$는 유일하다.

이제 이를 종합하면, 모든 $x, y \in V$에 대하여 $<T(x), y> = <x, T^*(y)>$를 만족하는 선형변환 $T^*: T\to T$가 유일하게 존재한다는 것을 알 수 있다. 이대 이 선형연산자 $T^*$를 $T$의 수반연산자라 한다. 이를 식으로 간단히 나타내면 다음과 같다.

수반 연산자에 대해 한가지 주의할 점은 모든 연산자에 대해 수반연산자가 존재하지 않는다는 점이다. 앞서 정리 1 에서 가정했듯이 유한차원의 연산자에 대해서만 수반연산자가 항상 존재함을 보장할 수 있다.

2. 수반연산자의 성질

정리 3. 유한차원 벡터공간 $V$와 $V$의 정규직교기저 $\beta$, $V$의 선형연산자 $T$에 대하여 다음이 성립한다.

증명
$A = [T]_\beta, B = [T^*]_\beta, \beta = \{v_1, v_2, \dots, v_n\}$이라 ㅎ자. 이때, $B_{ij}$는 다음과 같이 연결될 수 있다.

즉, $B = A^*$이다.

따름정리 $n\times n$행렬 $A$에 대하여 $L_{A^*} = (L_A)^*$이다.

이는 위의 정리로부터 자연스럽게 나오게 된다.
증명
$F^n$의 표준 순서기저를 $\beta$라 하자. 이때, $[L_A]_\beta = A$이므로 다음과 같이 정리할 수 있다.

지금까지의 정리를 살펴보면 복소수의 켤레복소수와 선형연산자의 수반연산자는 매우 닮았다는 것을 알 수 있을 것이다. 이를 정리해보자면 다음과 같다.

정리 4. 내적공간 $V$와 수반연산자가 존재하는 선형연산자 $T, U$에 대하여 다음이 성립한다.
1. $T + U$의 수반연산자는 존재하고 $(T+U)^* = T^* + U^*$이다.
2. 임의의 $c\in F$에 대하여 $cT$의 수반연산자가 존재하고, $(cT)^* = \bar{c}T^*$이다.
3. $TU$의 수반연산자가 존재하고, $(TU)^* = U^*T^*$이다.
4. $T^*$의 수반연산자가 존재하고 $T^** = T$이다.
5. $I$의 수반연산자가 존재하고 $I^* =I$이다.

또한 행렬에 대해서도 동일한 성질들을 가지게 되는데 잠깐 정리해보면 다음과 같다.

따름정리 $n\times n$행렬 $A$와 $B$에 대하여 다음이 성립한다.
1. $(A+B)^* = A^* + B^*$
2. $c\in F$에 대하여 $(cA)^* = \bar{c}A^*$
3. $(AB)^* = B^*A^*$
4. $A^{**} = A$
5. $I^* = I$

3. 최소제곱법

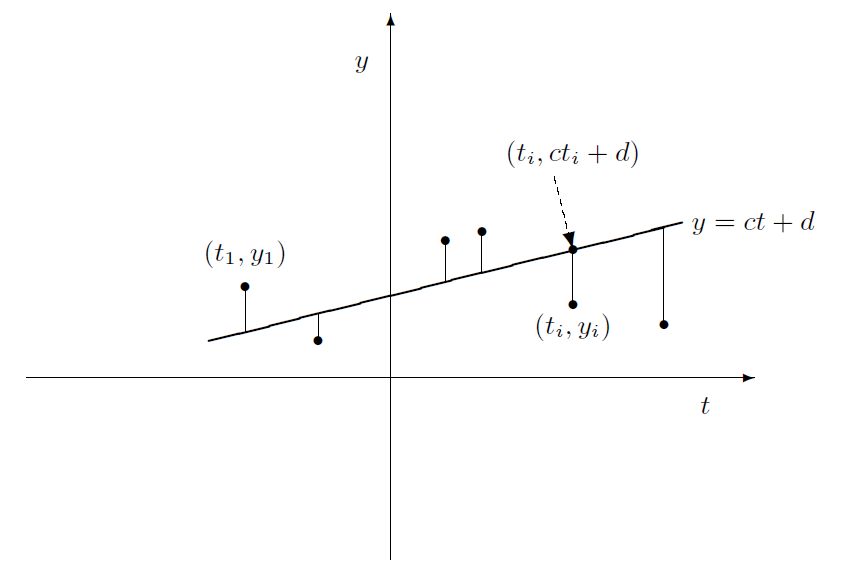
잠시 위와 같은 상황을 가정해보자. 즉, 선형회귀식을 살펴보자. 우리는 결국 $y = ct + d$를 만족하는 $a, b$를 찾고 싶다. 이때 $y, t$등의 관측치는 상수로 간주할 수 있다. 하지만 관측치는 모두 약간의 잔차를 가질 수 밖에 없고, 그 회귀식은 완전히 적합되지 못한다. 즉, 연립일차방정식의 해가 존재하지 않는 상황이다.

하지만 이런 상황에서도 최대한 적합한 식을 찾아야 한다. 이때 적합도는 다음과 같은 식을 통해 측정된다.

이때, 회귀식 $y =ct + d$를 최소제곱 직선이라고 부른다.

이를 관측치에 적용한 식은 다음과 같은 행렬과 벡터로 표현할 수 있다.

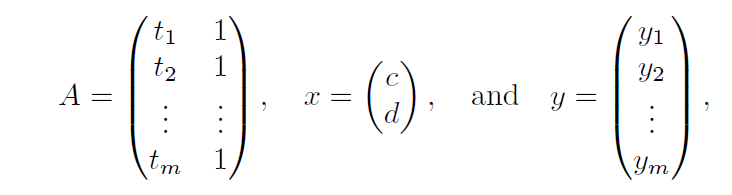
이때 오차는 $E = ||y-Ax||^2$으로 표현할 수 있다. 이제 우리는 $E$를 최소화하는 벡터 $x_0 \in F^n$을 찾아야 한다. 즉, 주어진 $m \times n$행렬 $A$와 모든 벡터 $x \in F^n$에 대하여 $||y-Ax_0|| \leq ||y-Ax||$를 만족하는 벡터 $x_0 \in F^n$를 찾고 싶은 것이다. 이에 성공하면 $k$차 다항식에 적합할 방법도 알 수 있을 것이다.

두 벡터 $x, y \in F^n$의 표준 내적을 $<x, y>_n$으로 표기하고, $x, y$을 열벡터로 취급하면 $<x, y>_n = y*x$임을 확인해보자.

보조정리 1. $A \in M_{m \times n}(F), x \in F^n, y \in F^n$에 대해 다음이 성립한다.

증명
이는 내적의 성질을 이용하면 쉽게 정리 가능하다.

보조정리 2. $A \in M_{m \times n}(F)$에 대하여 $rank(A^*A) = rank(A)$이다.

증명
이전에 증명한 차원정리에서 $x \in F^n$에 대해 $A^*Ax = 0$이기 위한 필요충분조건이 $Ax = 0$임을 보이면 될 것이다(역으로 말하면, $A^*A$와 $A$의 영공간이 같다.). $Ax = 0$은 결국 $A^*Ax = 0$을 내포하기 때문에, $A^*Ax =0$이라 가정하면 다음을 쉽게 보이게 된다.

즉, $Ax = 0$이 된다.

따름정리 $rank(A) = n$인 $m\times n$ 행렬 $A$에 대하여 $A^*A$는 항상 가역이다.

이제 $m\times n$ 행렬 $A$와 $y \in F^n$에 대해 $W = \{Ax : x \in F^n\}$이라 정의해보자. 즉, $W = R(L_A))$이다. 이때 $y$와 가장 가까운 $W$에 속하는 벡터는 유일하기 때문에 이를 $Ax_0$라고 해보자. 이를 수식으로 나타내면 모든 $x \in F^n$에 대해 $||Ax_0 - y|| \leq ||Ax -y||$이어야 한다. 이는 $E$를 최소화하는 벡터이기도 하다. 직교여공간을 이야기하면서 봤듯이 $Ax_0 -y \in A^\bot$이다. 다른말로하면 모든 $x \in F^n$에 대해 $<Ax, Ax_0 - y> =0$이다. 이때 보조정리 1을 이용하면 $<x, A^*(Ax_0 - y)> = 0, A^*(Ax_0 -y) =0$이 된다. 이제 이 식을 풀어 해를 구하면 된다. 이때 $rank(A) =n$라는 .가정을 추가하면 다음과 같이 정리 된다.

이제 우리는 회귀식을 적합할 수 있게 되었다.
이를 정리하면 다음과 같다.

정리 5. $A \in M_{m \times n}(F), y \in F^n$이 주어지면, 모든 $x \in F^n$에 대해 $||Ax_0 -y||\leq ||Ax -y||$이며, $(A^*A)x_0=A^*y$인 벡터 $x_0 \in F^n$이 존재한다. 특히 $rank(A) = n$이라면 $x_0 = (A^*A)^{-1}A^*y$로 정리된다.