1. Intro

이전에 벡터공간을 구성하는 기본 벡터를 기저라고 한다고 했다. 내적공간을 구성하는 기본조각은 정규직교집합인 기저가 된다. 이를 자세히 살펴보도록 하자.

정의 1. 내적공간 $V$의 부분집합이 정규직교집합인 순서기저 때, 이 부분집합을 정규직교기저라 한다.

이러한 정규직교집합과 정규직교기저가 중요한 이유는 이를 이용해 span을 표현하게 되기 때문이다.

정리 1. 내적공간 $V$와 0이 아닌 벡터로 이루어진 직교 부분집합 $S = \{ v_1, v_2 , \dots ,v_k\}$를 생각해보자. 이때, $y \in span(S)$에 대해 다음이 성립한다.

위 식의 의미는 후에 생각하기로 하고, 어떻게 유도되는지 먼저 살펴보자.
증명
$a_1, a_2, \dots, a_k \in F$에 대하여 $y = \sum^k_{i =1}a_iv_i$일 것이다. $i \leq j \leq k$일 때, $<y, v_j>$는 다음과 같이 나타낼 수 있다.

위 식을 다시 정리하게 되면, $a_j = {<y, v_j> \over ||v||^2}$ 이 된다. 이를 본래 기저의 스팬을 이용한 $y = \sum^k_{i=1}a_i, v_i$에 대입하면 위의 식이 성립하게 된다.

즉, 벡터 공간에서는 순서기저의 선형 결합을 통해 해당 공간의 벡터를 표현하게 되지만, 내적 공간에서는 서로 직교하는 벡터들의 성질을 이용해 직교 부분집합과 해당 벡터의 내적의 결합으로 표현할 수 있다. 다른 말로 하면, 해당 벡터와 직교하는 기저의 내적값에 정규화를 가한 스칼라 값이 해당 기저의 계수가 된다.

만약 해당 부분집합이 정규화된 정규직교집합이라면 다음 정리가 성립되게 된다.

따름정리 1. $S$가 정규직교집합이고, $y \in span(S)$일 때, 다음이 성립한다.

이 성질을 이용하면, 유한 정규직교기저를 가지는 내적 공간에 대해 쉽게 기저들의 계수를 구할 수 있게 된다. 단순히 정규직교기저와 해당 기저를 내적하면 되기 때문이다.

따름정리 2. 내적공간 $V$와 영이 아닌 벡터로 이루어진 직교 부분집합 $S$를 생각해보자. 이때, 집합 $S$는 항상 선형독립이다.

증명
$v_1, v_2, \dots, v_k \in S$이고, $\sum^k_{i=1}a_iv_i = 0$이라 가정해보자. 이때, $y = \sum^k_{i=1}{<y, v_i>\over||v_i||^2}v_i = a_iv_i = 0$이라 생각하면, 모든 $j$에 대하여 $a_j = {<0, v_j> \over ||v_j||^2} =0$이 된다.

2. 직교집합(그람-슈미트 직교화)

여기까지 오면, 정규직교기저를 가지는 내적 공간의 정규직교기저는 모두 선형 독립임을 알 수 있다. 그렇다면 모든 내적공간이 정규직교기저를 가지고 있는지 살펴보자.

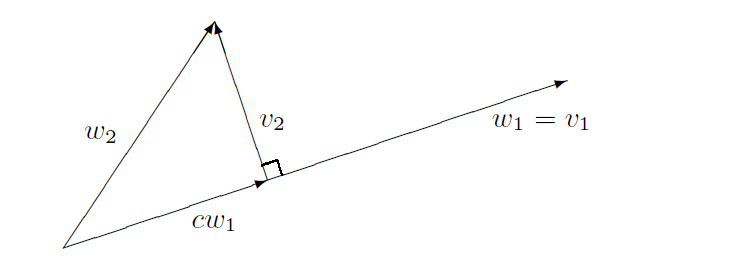
위와 같은 두 벡터 $w_1, w_2$를 가정해보자. 위의 내적공간에서 일차독립인 부분집합을 이루고 있다. 이때 이 부분공간을 생성하는 직교집합을 얻을 수 있다면, 정규직교기저를 쉽게 구할 수 있을 것이다. 위 그림에서 직교집합은 $v_1 = w_1, v_2 = w_2 - cw_1$으로 구할 수 있다. 이때, $c$는 $w_1$이 $v_2$와 직교하도록 하는 스칼라이다.

$c$의 값을 구하는 과정은 다음과 같다.

이제 이 과정을 일반화하여 보자.

정리 2. 내적공간 $V$의 선형독립인 부분집합 $S = \{w_1, w_2, \dots w_n\}$에 대하여 집합 $S' = \{v_1, v_2, \dots, v_n\}$을 다음과 같이 정의하자.

이때 $S'$는 $span(S') = span(S)$이고 0ㅇ이 아닌 벡터로 이루어진 직교집합이다.

즉, 순차적으로 각 선형독립의 벡터를 이전의 벡터를 이용해 직교하도록 하는 벡터를 찾는 방법을 사용하는 것이다. 증명해보도록 하자.

증명
집합 $S$를 구성하는 벡터의 개수를 $n$으로 놓고 이를 활용해 귀납법으로 증명할 것이다.
$k = 1, 2 \dots, n$에 대하여 $S_k = \{w_1, w_2, \dots , w_k\}$라 하자.
$n = 1$이라면, $S_1' = S_1$이라 하면 증명은 즉시 종료된다. 즉, $w_1 = v_1 \neq 0$인 경우이다.
이제 위의 정리를 이용하여 얻은 $S'_{k-1} = \{v_1, v_2, \dots, v_{k-1}\}$ 이 조건을 만족한다고 가정하고, $S'_k$가 조건을 만족하는지 살펴보도록 하자.
$v_k = 0$이라면, $0 = w_k - \sum^{k-1}_{j =1}a_jv_j$이므로, $w_k \in span(S'_{k-1}) = span(S_{k-1})$을 의미하게 된다. 이는 $S_k$가 선형독립이라는 가정을 위반하게 되므로 모순이 된다. 즉, $v_k \neq 0$이다.

따라서 $v_k \neq 0$이고, $S_k'$는 선형독립이다. 이를 식으로 전개해보면 다음과 같다.

위 수식에서 $<v_i, v_j> = 0 \quad (i \neq j)$는 $S'_{k-1}$이 직교집합이라 가정했기 때문이다.또한, $span(S'_k) \subseteq span(S_k)$이 정리의 식에 의해 성립하게 되고, 따름정리 2에 의해 $S'_k$는 선형독립이 된다.
위 결론들을 모두 종합하면 결국 $dim(span(S'_k)) = dim(span(S_k)) = k$이므로, $span(S'_k) = span(S_k)$가 된다.

위의 방식이 바로 그람-슈미트 직교화이다. 그람-슈미트 직교화는 주어진 내적공간에서 정규직교집합을 구할 수 있는 강력한 방법으로, 기저를 손쉽게 구할 수 있게 해준다.

3. 정규직교기저의 선형결합

그람-슈미트 직교화로 정규직교기저를 구했다면, 역으로 주어진 벡터를 어떻게 정규직교기저의 선형결합으로 나타낼 수 있을까?

정리 3. 점공간이 아닌 유한차원 내적공간 $V$는 정규직교기저 $\beta$를 포함한다. 특히 $\beta = \{v_1, v_2, \dots, v_n\}$일 때, $x \in V$에 대하여 $x = \sum^n_{i=1}<x, v_i>v_i$이다.

증명
이는 쉽게 증명이 가능하다. $V$의 순서기저 중 하나를 $\beta_0$라 하자. 이때, 그람슈미트 직교화를 통해 직교집합 $\beta'$를 얻을 수있다. $span(\beta') = span(\beta_0) = V$이다. 이렇게 얻은 직교집합 $\beta'$를 정규화하면 정규직교집합 $\beta$를 얻을 수 있게 된다. 이 정규직교집합은 따름정리 2에서 보인바와 같이 선형독립이므로, 정규직교기저 정의에 의해 $\beta$는 $V$의 정규직교기저가 된다. 그리고, 따름정리 1을 통해 위와 같은 식으로 선형결합을 표현할 수 있다.

따름정리 3. 정규직교기저 $\beta = \{v_1, v_2, \dots, v_n\}$을 포함한 유한차원 내적공간 $V$와 선형연산자 $T$를 생각해보자. $A = [T]_\beta$일 때, 임의의 $i. j$에 대하여 $A_{ij} = <T(v_j), v_i>$이다.

이는 쉽게 유도되는데, 정리 3에 의해 $T(v_j) = \sum^n_{i=1}<T(v_j),v_i>v_i$이다. 이를 풀어서 쓰게 되면, $A_{ij} = <T(v_j), v_i>$가 된다.

즉, 선형연산자의 정규직교기저에 대해 행렬표현의 성분 역시 그람슈미트 직교화를 통해 쉽게 구할 수 있다.

4. 정사영

정의 2. 내적공간 $V$의 공집합이 아닌 부분집합 $S$에 대하여, $S$의 모든 벡터와 수직인 벡터의 집합을 $S^\bot$라 하자. 즉, $S^\bot = \{x \in V: 모든 \quad y \in S에 \quad에 대하여 <x, y> = 0\}$이다. 집합 $S^\bot$를 $S$의 직교여공간이라 한다.

직교여공간은 여러모로 유용한 개념인데, 특히 선형회귀와 관련이 있어 자세히 다룰 필요가 있다.

위와 같이 $R^3$에서 점 $P$와 평면 $W$ 사이의 거리를 구하는 문제를 생각해보자. 이는 선형회귀에서 잔차가 z인 상황에서 $u$로 적합시키는 상황이라고 볼 수 있다. 이는 두점 $0, P$로 결정되는 벡터를 $y$라 하면, 주어진 문제를 다음처럼 나타낼 수 있게 된다.

$W$의 벡터 중 $y$와 가장 가까운 벡터 $u$를 찾아라.

이 문제에서 우리가 구하고자 하는 거리는 $||y -u||$가 된다. 이때 벡터 $z$는 그림에서 보이듯이 $W$의 모든 벡터와 수직이게 된다. 즉, 여기서 직교여공간이 등장한다. $z \in W^\bot$이다.

정리 4. 내적공간 $V$의 유한차원 부분공간 $W$와 벡터 $y \in V$에 대하여 $y = u +z$인 유일한 벡터 $u \in W$와 $z \in W^\bot$이 존재한다. 또한, $\{v_1, v_2, \dots, v_k\}$가 $W$의 정규직교기저일때, 다음이 성립한다.

이때 이전과 다른 점은 $y$가 $W$에 있지 않더라도 해당 식이 성립한다는 것이다. 즉, 기존에는 $y$가 속한 공간을 구성하는 정규직교기저의 선형 결합을 통해 $y$를 표현하는 방법을 다뤘다면, 이번에는 $y$가 속한 공간의 부분공간에 대해서 다루게 된다는 뜻이다.
증명
$W$의 정규직교기저 $\{v_1, v_2, \dots, v_k\}$와 앞서 서술한 벡터 $u$를 $z = y -u$라 하자. 이때, $u \inW, y = u +z$이다.

우리는 $z \in W^\bot$을 보이면 된다. 이는 $z$가 모든 $v_j$에 대해 수직임을 보이면 충분하다. 임의의 $j$에 대하여 다음이 성립한다.

즉, $z$는 모든 $v_j$와 직교한다. 즉, $z \in W^bot$이다

이제 이러한 조건을 만족하는 $u$와 $z$가 유일함을 보이면 된다. $y = u+z = u'+z=, u' \in W, z\ \in W^\bot$이라 가정하면, $u -u' = z - z' \in W \cup W^bot = \{0\}$이 된다. 즉, $u = u', z = z'$일 수 밖에 없다.

이를 통해 내적공간 $V$의 부분공간 $W$ 밖에 위치한 벡터 $y \in W$와 가장 거리가 가까운 벡터 $u$를 찾는 방법을 다뤄보았다. 이제 이 벡터에 대해 한가지의 성질만 더 살펴보고 마무리하도록 하자.

따름정리 4. 내적공간 $V$의 유한차원 부분공간 $W$와 벡터 $y \in V$에 대하여 $y = u+z$이고, $z \in W^\bot$임을 우리는 알고 있다. 이때, $u$는 $W$의 벡터 중 $y$에 가장 가까운 유일한 벡터이다. 다시 말해, 임의의 $x \in W$에 대하여 $||y-x|| \geq ||y -u||$이다. 등호는 $x = u$일 경우에만 성립하게 된다.

증명
이미 우리는 $y = u+z$이고, $z \in W^bot$임을 알고 있다. $x \in W$에서 $u -x$는 $z$와 직교한다. 이때 $y$와 $x$의 거리는 다음과 같다.

만약 $||y-x|| = ||y-u||$라면 위 식의 부등호는 등호로 바뀌게 된다. 즉, $||u-x|| = 0 \leftrightarrow x = u$를 얻게 된다.

이 따름정리에서 나오는 벡터 $u$를 $y$의 $W$에 대한 정사영이라 한다. 벡터의 정사영은 정말 많이 사용된다. 이 개념 자체는 선형회귀 외에도 mapping 함수의 개념과도 연관되게 된다.

5. 정규직교기저의 성질

이전에 임의의 유한차원 벡터 공간에서 일차독립인 부분집합은 기저로 확장됨을 확인했었다. 이는 유한차원 내적공간에서 정규직교 부분집합에 대해서도 비슷한 결과를 가지게 된다.

정리 5. $n$차원 내적공간 $V$의 정규직교집합 $S = \{v_1, v_1, \dots, v_k\}$에 대해 다음이 성립한다.
1. $S$를 확장하여 $V$의 정규직교기저 $\{v_1, v_2, \dots, v_k, v_{k+1}, \dots, v_n\}$을 얻을 수 있다.
2. $W = span(S)$일 때, $S_1 = \{v+{k+1}, v_{k+2},\dots, v_n\}$은 $W^\bot$의 정규직교기저이다.
3. $V$의 임의의 부분공간 $W$에 대하여 $dim(V) = dim(W) + dim(W^\bot)$이다.