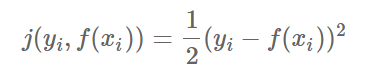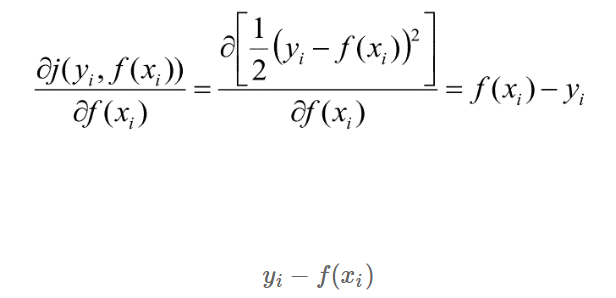CV study 2. Bayesian, Boosting

skh951225·2022년 10월 9일

Bayesian vs Frequentist

Frequentist

Data vary(=random)
Parameter fixed(=random x)
ex) 동전을 던졌을때 앞면이 나올 확률이 0.5이다.
빈도주의적 관점에서는 데이터에 불확실성(Uncertainty)가 있고 이로인해 무작위성(Randomness)이 발생한다고 생각한다. 이렇게 데이터에 무작위성이 포함되는 불확실성을 Aleatoric uncertainty 라고 한다.
그래서 빈도주의적 관점에서 확률은 무한히 많은 시행을 통해 구할 수 있다.
$P(heads) = \displaystyle\lim_{n\to\infin} {N(heads)\over n}$

Baysian

Data fixed(=random x)
Parameter vary(=random x)
Baysian 관점에서는 parameter가 확률 분포로 존재하며 이를 prior distribution이라고 한다.
Baysian 관점에서의 불확실성은 지식(정보)의 부족으로 인해 발생하며 epistemic uncertainty 라고한다.
prior distribution과 data를 통해 posterior distribution을 구할 수 있고 이 값을 prior distribution으로 갱신함으로써 지식(정보)의 습득으로 인해 불확실성을 낮출 수 있다.

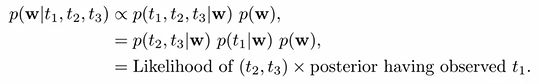
Baysian theorem
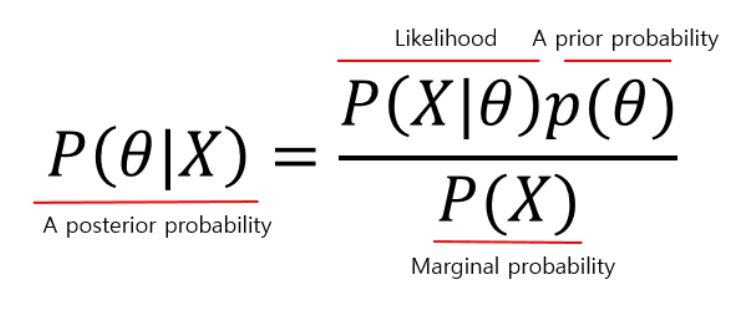
X: 관측된 데이터, Observation을 뜻한다. 우리가 갖고 있는건 이거다!! (머신러닝에서는 트레이닝 데이터.....)
Θ: Hypothesis를 말하는데 데이터를 통해 추정하고자 하는 값이 되겠다. classification문제에서는 각 discrete한 클래스가 될 수 있고 linear regression의 경우 추정하려고 하는 weight들이 될 수 있다. 그 외에 추정하고자 하는 모든 문제에서 추정하고싶은 target값이 된다.
Marginal probability P(X): 데이터 X자체의 분포를 뜻한다.
A prior probability(사전확률) P(Θ): 사전에 가지고 있는 확률을 말한다. 이때 Θ는 mutually independent해야한다.예를들어. "하늘이 파랗다"/"하늘이 파랗지 않다" 이 두가지 가정은 독립이고 두 확률의 합이 1이 되어야한다. (사전적으로 hypothesis에 대한 지식이 없을 때는 그냥 hypothesis의 element들이 가질 확률이 모두 같다고 두자)
Likeihood(우도) P(X|Θ): hypothesis를 두고, 다시말해 어떤 가정을 한 상태의 데이터의 분포를 뜻한다.
A posterior probability(사후확률) P(Θ|X): observation이 주어졌을 때의 hypothesis의 분포를 뜻한다. 얘같은 경우에는 데이터 X의 영향을 반영하는 애다.

MLE, MAP

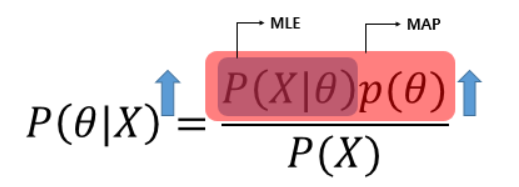
MLE 와 MAP 는 근본적으로 사후확률을 최대화하기 위해 사용되는 방법이다. 사후확률을 바로 구하기 어려울때 좌변의 값을 통해 구하겠다는 것인데, MLE는 가능도를 최대화 하여 그 목적을 달성하고 MAP는 가능도와 사전확률의 곱을 최대화하는 방법이다. MLE 는 사전확률에 대한 정보가 없을때 이유 불충분의 원리에 의해 사전확률이 균등한 확률을 가진다는 가정을 하기때문에 가능도만을 가지고 우변을 최대화 할 수 있다.

Boosting

여러 개의 learning 모델을 순차적으로 구축하여 최종적으로 합침(앙상블)
여기서 사용하는 learning 모델은 매우 단순한 모델
순차적 -> 모델 구축에 순서를 고려
각 단계에서 새로운 base learner를 학습하여 이전 단계의 base learner의 단점을 보완
각 단계를 거치면서 모델이 점차 강해짐 -> boosting
Boosting 알고리듬의 종류
- Adaptive boosting(Adaboost)
- Gradient boosting machines(GBM)
- XGboost
- Light gradient boost machines(Light GBM)
- Catboost

AdaBoost

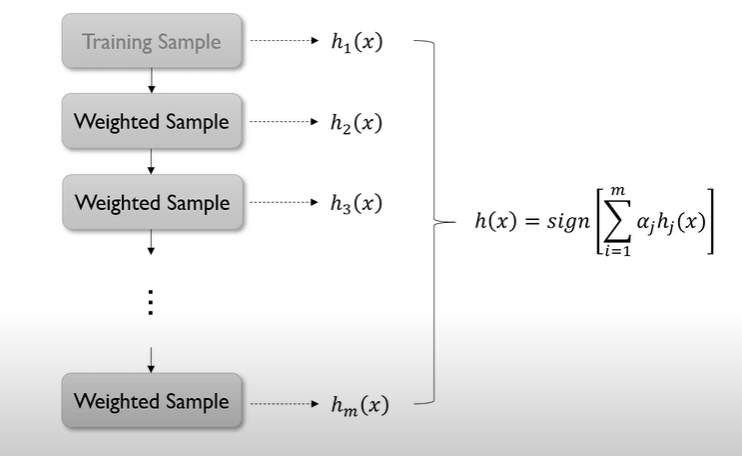
각 단계에서 새로운 base learner를 학습하여 이전 단계의 base learner의 단점을 보완
Training error가 큰 관측치의 선택확률(가중치)을 높이고, training error가 작은 관측치의 선택확률을 상대적으로 낮춤
앞 단계에서 조정된 확률(가중치)을 기반으로 다음 단계에서 사용될 training dataset 구성
다시 첫단계로 감
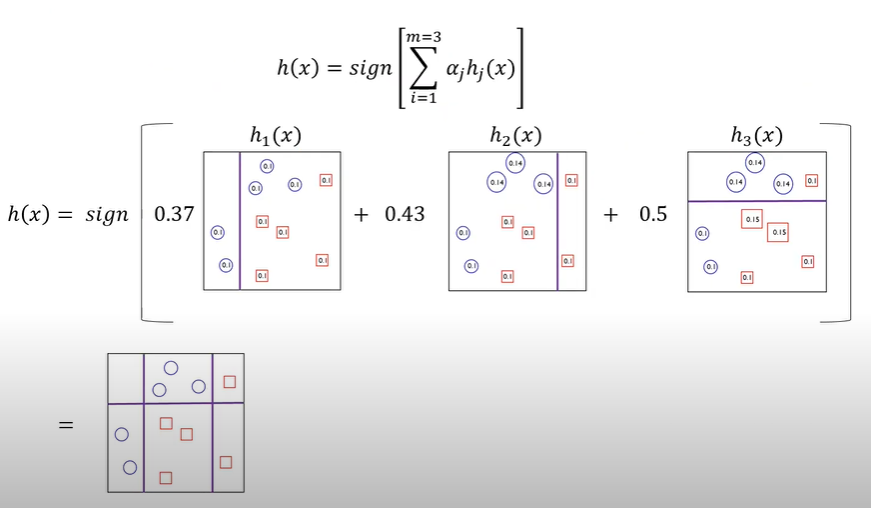
최종 결과물은 각모델의 성능지표를 가중치로 하여 결합 (앙상블)

AdaBoost algorithm

step 1

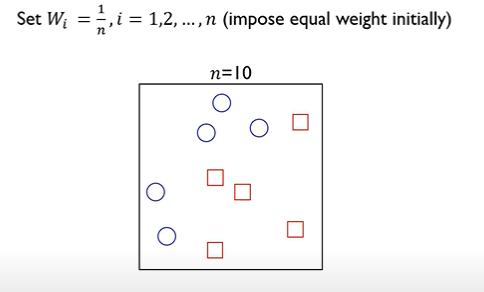
step 2

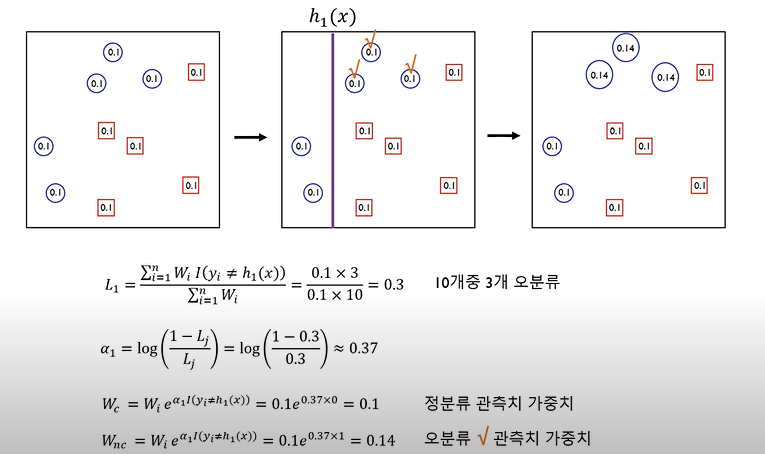
step 3

GBM

Gradient boosting = Boosting with gradient decent
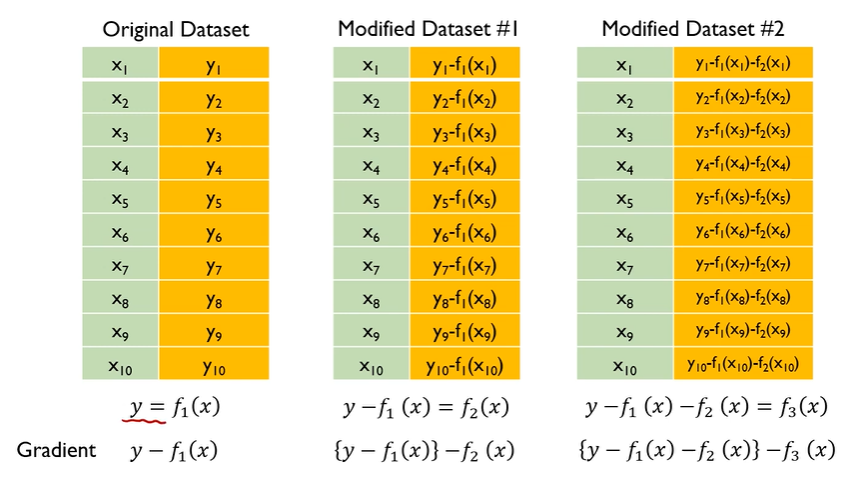
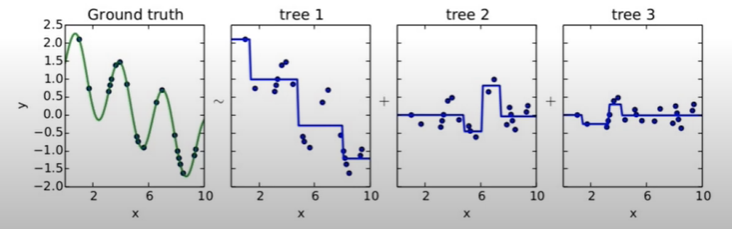
첫번째 단계의 모델 tree 1 을 통해 Y를 예측하고, Residual을 다시 두번째 단계 모델 tree 2 를 통해 예측하고, 여기서 발생한 Residual을 모델 tree 3로 예측
점차 residual이 작아짐
Gradient boosted model = tree 1 + tree 2 + tree 3