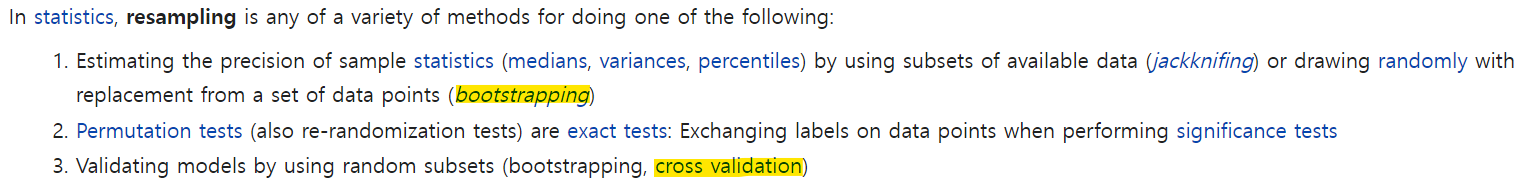CV study(1. Resampling, p-value, KL divergence)

Resampling

출처

왜 사용하는가?

리샘플링은 모집단의 분포 형태를 알 수 없을 때 주로 사용하는 방법이다. 즉, 모분포를 알 수 없으므로 일반적인 통계적 공식들을 사용하기 힘들 때, 현재 갖고 있는 데이터를 이용하여 모분포와 비슷할 것으로 추정되는 분포를 만들어 보자는 것이다. 리샘플링은 가지고 있는 샘플에서 다시 샘플 부분집합을 뽑아서 통계량의 변동성(variability of statistics)을 확인하는 것이라고 할 수 있다. 즉, 같은 샘플을 여러 번 사용해서 성능을 측정하는 방식이다.

Bootstrapping

부트스트랩이라는 말은 ‘자기 스스로 하는’, ‘독력(獨力)의’라는 뜻을 가진 단어이다.

다시 말해 주변의 도움 없이 스스로 해낸다는 의미인데, 컴퓨터의 부팅이 bootstrapping을 줄인 말이라는 것은 잘 알려져있는 사실이기도 하다.

영단어 bootstrap의 어원은 부츠 신발의 등쪽에 달려있는 끈을 얘기하는데,
<허풍선이 남작의 모험> 에 나오는 일화에서 남작이 늪에 빠졌을 때 부츠 등의 끈을 잡고 스스로 빠져나왔다는 어처구니 없는 이야기에서 유래됐다는 설이 있다.

Bagging vs Boosting

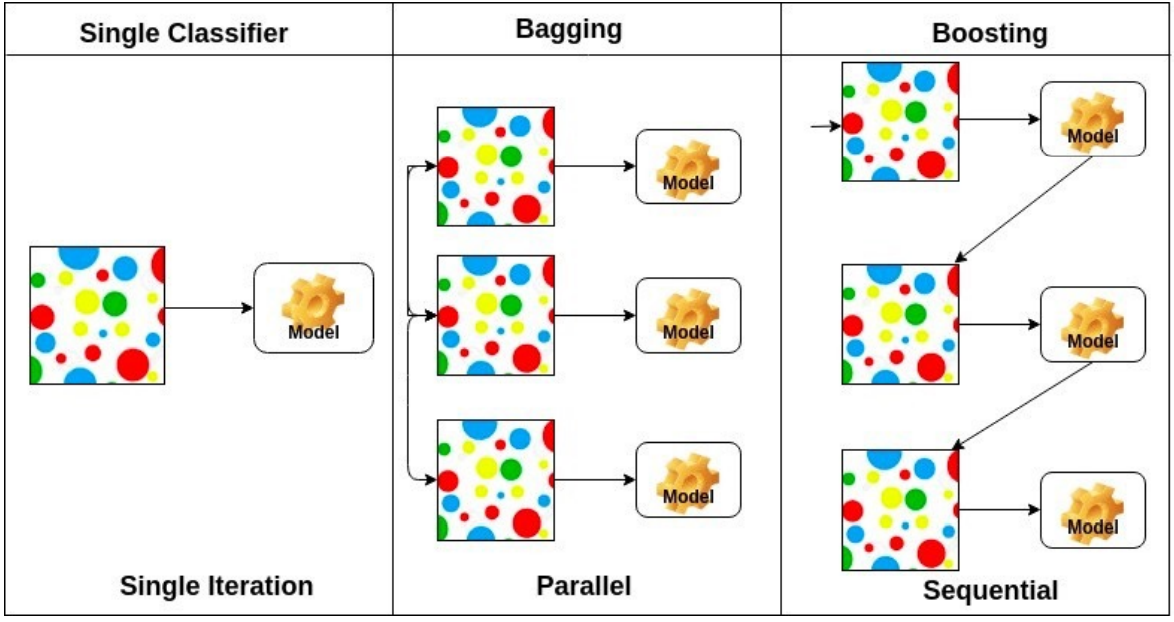
Bagging (Bootstrapping aggregating)

• Multiple models are being trained with bootstrapping
• ex) Base classifiers are fitted on random subset where individual
  predictions are aggregated (voting or averaging).

Boosting

• It focuses on those specific training samples that are hard to classify
• A strong model is built by combining weak learners in sequence
  where each learner learns from the mistakes of the previous weak
  learner.

p-value

대립가설 vs 귀무가설

출처

• 대립가설 : 우리가 증명 또는 입증하고자 하는 가설
• 귀무가설 : 우리가 증명하고자 하는 가설의 반대되는 가설

1종 오류 vs 2종 오류

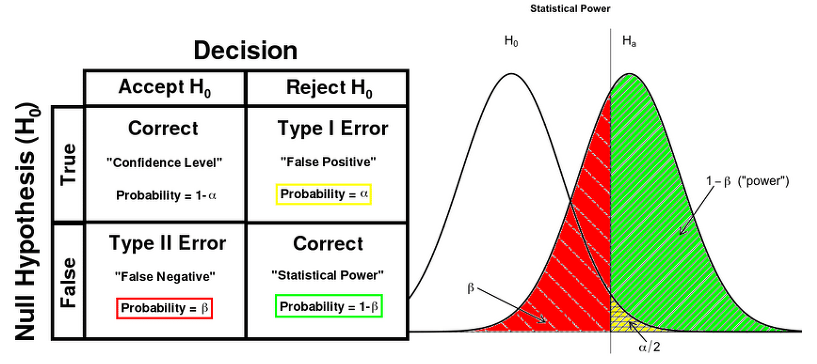
1종 오류 : 귀무가설이 참일때 기각할 경우

• 유의수준($\alpha$) : 귀무가설이 참일때 기각할 상한선

2종 오류 : 귀무가설이 거짓일때 채택할 경우

• 검정력($1-\beta$) : 대립가설이 참일때 귀무가설을 기각할 확률

p-value

귀무가설이 옳다는 가정하에 검정 통계량이 구해질 확률, 결국 p-value가 유의수준($\alpha$) 보다 작다면 귀무가설을 기각하게 된다.

KL divergence

출처

최대 가능도 추정법(Maximum Likelihood Estimation)

• 가능도(likelihood) 는 확률(probability) 와 다른 개념이다. 보통 확률 밀도함수나 확률 질량함수의 경우 모수가 정해졌을때 데이터에 따른 확률을 나타내지만 가능도 함수의 경우 데이터가 주어졌을때 모수에 따른 가능성을 나타낸다. 또한, 가능도 함수는 모수에 대해 적분을 하였을때 일반적으로 1이 되지 않는다.
  

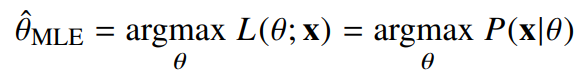
로그 가능도

• 데이터집합 X 가독립적으로추출되었을경우로그가능도를최적화합니다.
  

로그 가능도를 사용하는 이유는 여러가지가 있는데
(1) 로그가능도를최적화하는모수 는가능도를최적화하는MLE가됩니다.
(2) 데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수 억단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는것은 불가능합니다.
(3) 경사하강법으로 가능도를 최적화할때 미분연산을 사용하게 되는데,로그
가능도를 사용하면 연산량을 $O(n^2)$에서 $O(n)$으로줄여줍니다.

딥러닝에서 최대 가능도 추정법

• 딥러닝에서 분류문제를 풀때 아래와 같이 정답 레이블에 대한 로그 가능도를 최대화하는 모수를 구하는데 사용할 수 있다. 아래의 식은 크로스 엔트로피 라고도 부른다.
  

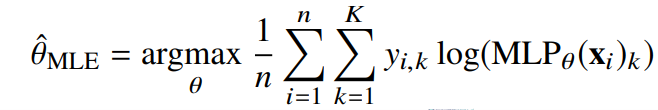
KL divergence

• 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터
  에서 관찰되는 확률분포의 거리를 통해 유도합니다.

• 데이터공간에 두 개의 확률분포 $P(x)$,$Q(x)$ 가 있을 경우 두 확률분포사이
  의 거리(distance)를 계산할때 다음과 같은 함수들을 이용합니다.
  - 총변동 거리(TotalVariationDistance,TV)
  - 쿨백-라이블러발산(Kullback-LeiblerDivergence,KL)
  - 바슈타인거리(WassersteinDistance)

• KL divergence는 다음과 같이 표현합니다.
  

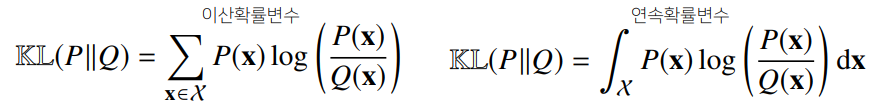
• 결국 분류문제에서 정답 레이블을 $P$,모델예측을 $Q$ 라고 두면 최대가능도추정법
  은 쿨백-라이블러발산을 최소화하는 것과 같습니다.