CV study 3 Optimization

목차

1. Lagrange multiplier 를 통해 equality constraint 가 포함된 최적화 문제를 푸는 방법
2. Lagrange multiplier 를 통해 최적화 문제를 풀기위해선 gradient가 0 이 되는 지점을 구해야하는데 함수의 차원이 높아지게 되면 그 지점을 찾기 어려워진다. 결국 알고리즘 적으로 접근하게 되는데, 그 방법으로 Newton's method와 Backtracking line search에 대한 설명
3. inequality constraint가 추가된 최적화 문제를 푸는 방법인 KKT condition에 대한 설명
4. 최적화 문제를 직접적으로 풀기 어려울때 Dual problem을 통해 Primal problem의 하한을 구하는 방법에 대한 설명
5. Convex Problem에 대해 KKT condition과 Optimal point와의 관계

1. Lagrange multiplier

$\nabla f(x^*)\cdot \vec u$ 의 의미

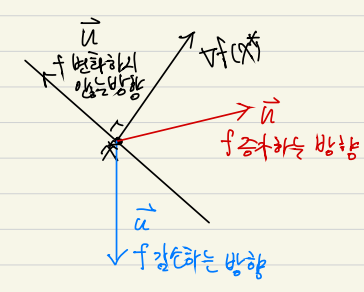
$\nabla f(x^*)\cdot \vec u = 0$ : $f$ 변화하지 않는 방향
$\nabla f(x^*)\cdot \vec u < 0$ : $f$ 감소하는 방향
$\nabla f(x^*)\cdot \vec u > 0$ : $f$ 증가하는 방향

$x=x^*$가 local minimum 이기 위한 필요조건

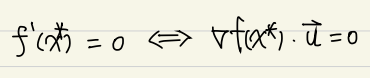
for $x^* +\delta \vec u \in dom f$

Lagrange multiplier

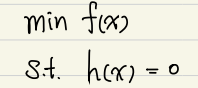
Equality constraint가 있을때 함수 $f(x)$ 를 최소화 시키는 최적점의 후보군을 찾는 방법론

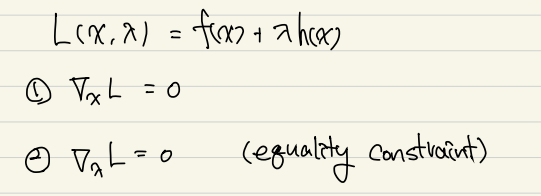
1번과 2번을 연립하여 local minimum이기 위한 필요조건을 만족하는 x와 lambda를 구하고 이렇게 구한 x를 f(x)에 대입하여 f(x)를 최소화 시키는 x를 찾는다.

$\nabla_x L = 0$ 증명

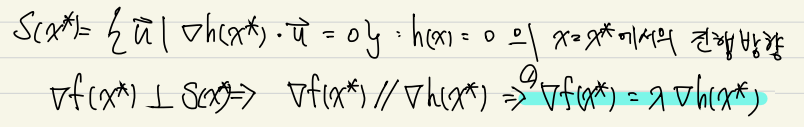
Lagrange multiplier 예제

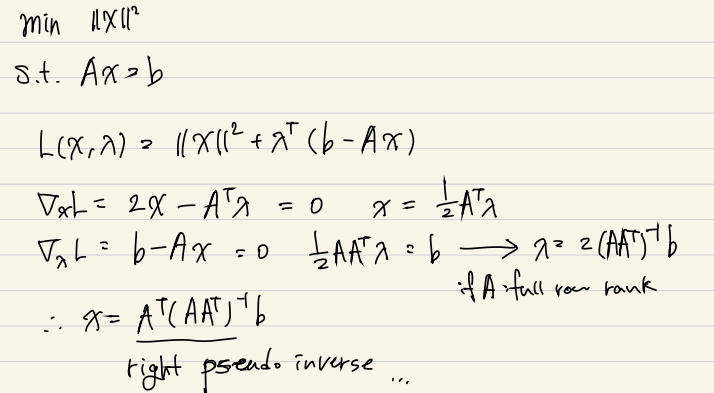
2. Lagrange multiplier 알고리즘 적으로 풀기

Lagrange multiplier를 적용하게 되면 gradient가 0 이 되는 지점을 찾아야한다.
하지만 Lagrangian function의 차수가 높아지게 되면 gradient가 0 이 되는 지점을 찾기 쉽지 않다. 따라서 보편적으로 그러한 경우 알고리즘을 통해 풀게 된다.

Newton's method

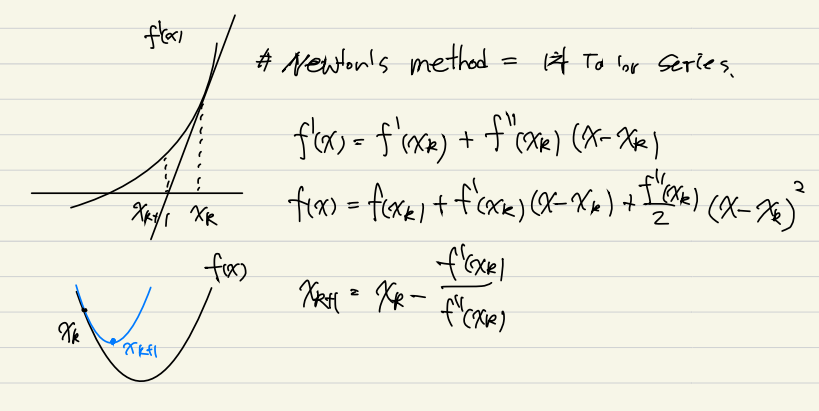
Newton's method 는 반복적인 1차 Taylor 근사를 통해 함수 값이 0이 되는 지점을 찾는 방법이다.

Newton's method 를 Lagarange multiplier 에 적용

w의 초기값이 constraint를 만족하지 않아도 되므로 이 방법론을 Infeasible start Newton method라고 부른다.

Backtracking line search

참고자료
Gradient descent에서 고정 step size를 사용하게 되면 진행 속도가 항상 동일하기 때문에, 경사가 가파른 구간에서는 최적점을 지나쳐서 진동할 수 있으며 경사가 평평한 구간에서는 진행이 느려질 수가 있다. 따라서, 곡면의 특성에 맞춰 속도를 조절하면서 진행해야 수렴도 보장되고 수렴 속도도 높아진다. 이와 같이 곡면의 특성에 맞춰 step size를 적응적으로 선택하는 방법 중 하나가 backtracking line search이다.

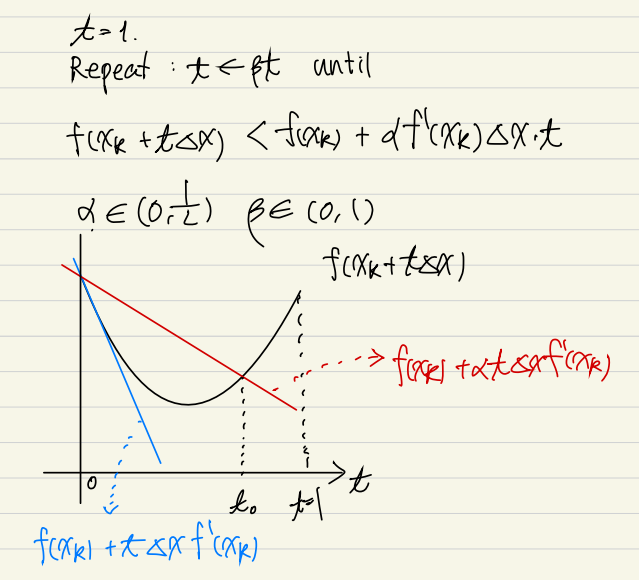
$\alpha$ 와 $\beta$ 는 모두 hyperparameter인데 $\alpha$의 경우 얼마나 빡빡하게 최적점을 찾을 것인가에 대한 것이고 $\beta$ 는 t를 업데이트할때 얼마나 줄여나갈것인가에 대한 값이다.

3. KKT condition

inequality constraint가 추가된 최적화 문제의 local minimum의 필요조건

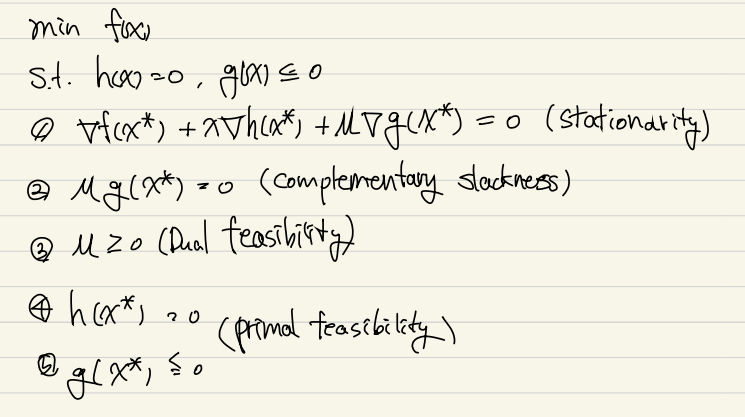
1번, 3번 조건 증명

2번 조건 증명

g(x) 의 경계에 있을때 g(x)=0 이므로 만족하게 되고, g(x) 내부에 local minimum이 존재하게 되면 inequality constraint를 고려하지 않아도 되므로 $\mu=0$ 가 되어 만족하게 된다.

Regularity condition

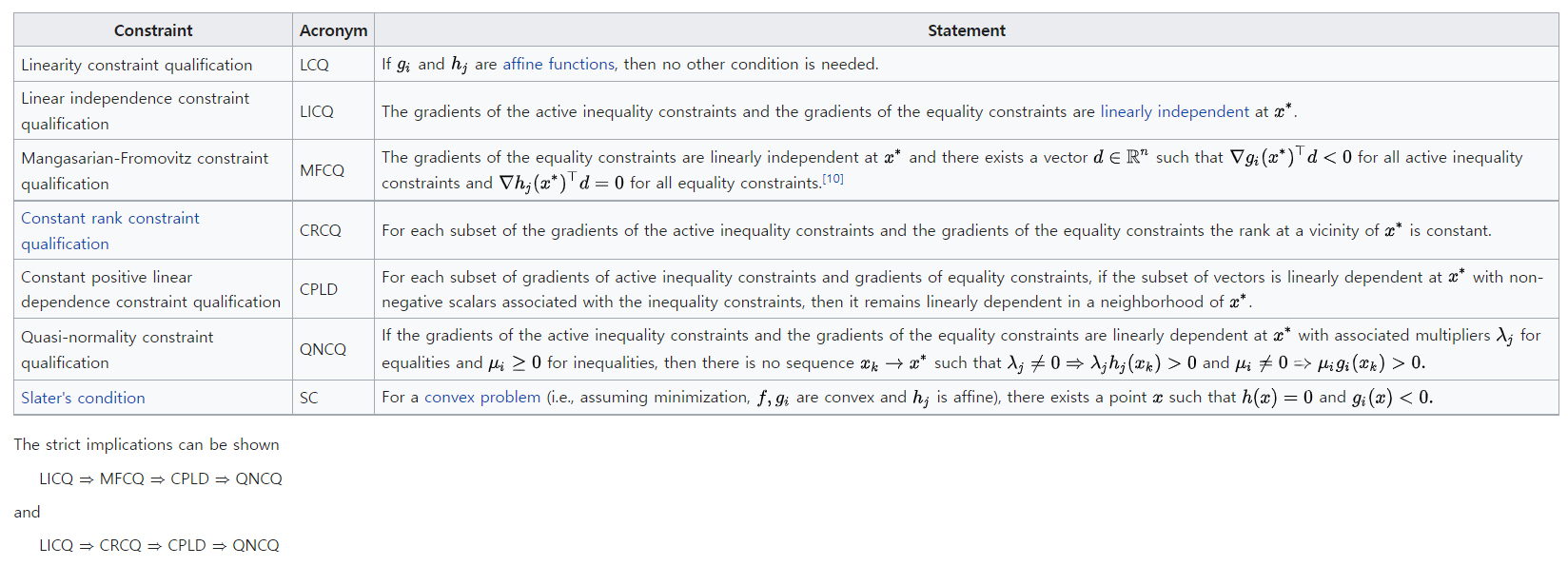
constraint 가 여러개일 경우 위의 조건중 하나만 만족하게 되면 kkt condition 이 local minimum이기 위한 필요조건이 성립하게된다. 특히, Slater's condition을 만족하게 되면 Strong duality가 성립한다.

4. Duality

직접적으로 목적함수를 최적화 시키는 Optimal을 찾기 어려울때 duality를 이용하여 Optimal value의 lower bound를 구할 수 있다.

우리가 풀고자하는 최적화 문제를 Primal problem이라고 하고 Lagrangian function을 x 에 대해 minimize하는 함수를 Lagrangian dual function, 최대화하는 최적화 문제를 Lagrange dual problem 이라고 한다.

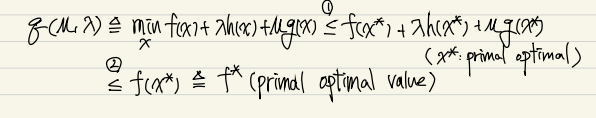
Lagrangian function을 x 에 대해 minimize하는 함수를 통해 $f^*$, 즉 주어진 조건을 만족하는 f(x)의 최소값의 lower bound를 구할 수 있다. 모든 $0\le \mu,\lambda$ 에 대해 위의 관계를 항상 만족하므로 $q(\mu,\lambda)$ 를 최대화 하는 $q^*$(Dual optimal value)또한 $f^*$ 보다 항상 작거나 같다.

결과적으로 $q^*$ 를 통해 best lower bound를 구할 수 있다.

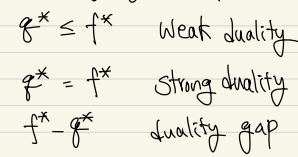
$f^*$ 가 $q^*$ 크거나 같은 것을 weak duality, 같을 때 strong duality, 두 값의 차이를 duality gap이라고 한다. 만약 $q(\mu,\lambda)=f(x)$ 를 만족하는 feasible 한 $\mu,\lambda,x$ 를 구할 수 있다면 $\mu,\lambda,x$는 optimal이며 Strong duality를 만족한다.

증명

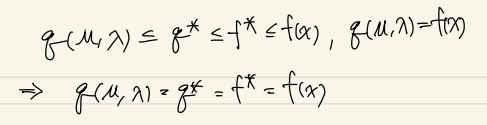
Duality 를 활용하는 이유

Primal problem을 직접적으로 풀기 어려울때가 많고 dual problem을 푸는 것은 상대적으로 쉽다. 왜냐하면 Lagrangian dual function 은 Concave 함수이기 떄문이다.

Concave 증명

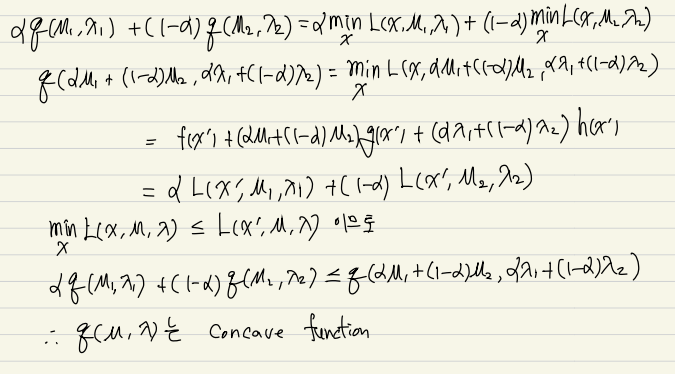
5. Convex problem

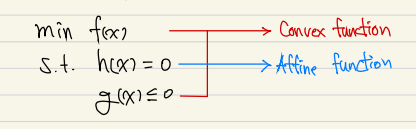
위 와 같이 목적함수와 inequality function이 convex function이고 equality constraint가 affine function인 문제를 convex problem이라고 한다.

$KKT\Rightarrow Optimal$

Convex problem에 대해 KKT condition을 만족하게 되면 Optimal이다.

증명

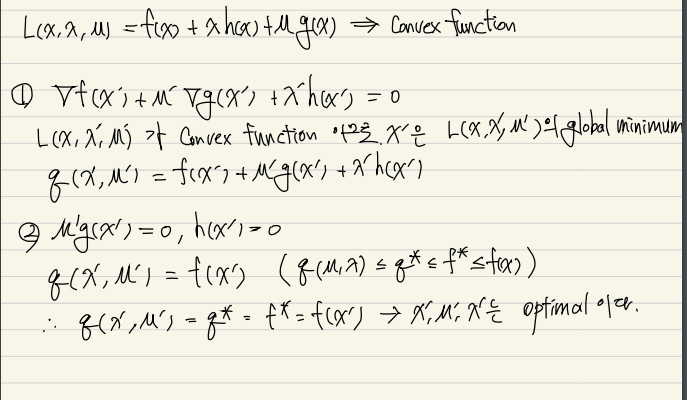
$KKT \Leftrightarrow Optimal$(Slater's condition)

Slater's condition을 만족하는 문제에 대해 KKT condition과 Optimal은 필요충분조건이다.

$KKT\Rightarrow Optimal$

Slater's condition은 convex를 전제로 하기때문에 만족한다.

$KKT\Leftarrow Optimal$

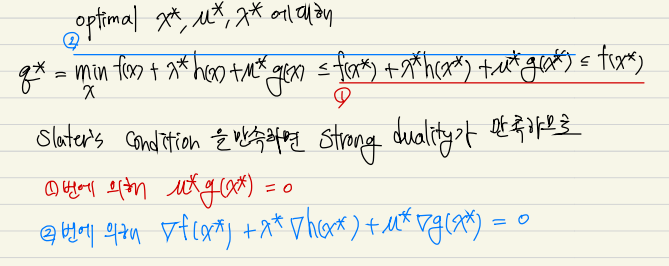
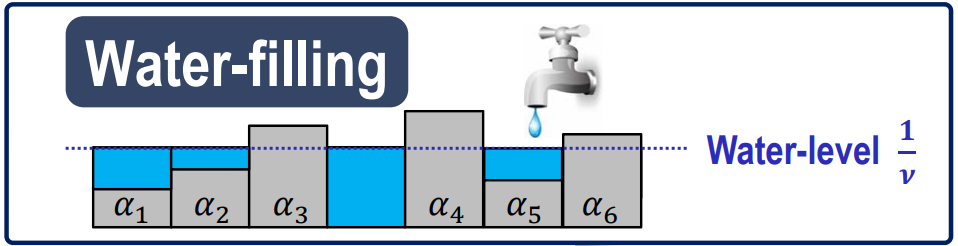
Convex problem 예제

참고자료

1. Lagrange multiplier 를 통해 equality constraint 가 포함된 최적화 문제를 푸는 방법
2. Lagrange multiplier 를 통해 최적화 문제를 풀기위해선 gradient가 0 이 되는 지점을 구해야하는데 함수의 차원이 높아지게 되면 그 지점을 찾기 어려워진다. 결국 알고리즘 적으로 접근하게 되는데, 그 방법으로 Newton's method와 Backtracking line search에 대한 설명
3. inequality constraint가 추가된 최적화 문제를 푸는 방법인 KKT condition에 대한 설명
4. 최적화 문제를 직접적으로 풀기 어려울때 Dual problem을 통해 Primal problem의 하한을 구하는 방법에 대한 설명
5. Convex Problem에 대해 KKT condition과 Optimal point와의 관계