RWKV: Reinventing RNNs for the Transformer Era
Problem posing
Limitations of Transformer
Transformer는 NLP에서 엄청난 파급력을 지녔지만 memory와 time complexity 측면에서 부담스럽다. Transformer 모델은 의 Time complexity를 지녔고 의 Space complexity를 지녔다.
그 말은 즉 sequence length가 길어질수록 그에 제곱에 해당하는 크기quadratic complexity로 시간이 오래걸리고 메모리를 많이 차지한다는 것이다.
Limitations of RNNs
그렇다면 RNN은 어떨까. RNN은 의 Time complexity와 의 Space complexity를 지니고 있기 때문에 Transformer보다 resource-friendly 하다고 할 수 있다. 하지만 parallelization 측면에서 Transformer는 아주 큰 블럭의 attention을 한번에 계산하는 반면 RNN은 모든 sequence를 하나씩 계산해나가야하기 때문에 떨어진다고 할 수 있다. 또한 RNN은 scalability 측면에서도 떨어지기 때문에 이제까지 빛을 받지 못하였다.
또한 RNN은 고질적으로 vanishing gradient problem을 가지고 있는데, 이는 RNN의 특성상 sequence 하나하나를 순차적으로 계산하기 때문에 발생한다. 이는 모델을 훈련할때 아주 긴 sequence의 텍스트를 훈련하는 데에 어려움을 준다.
Related Works
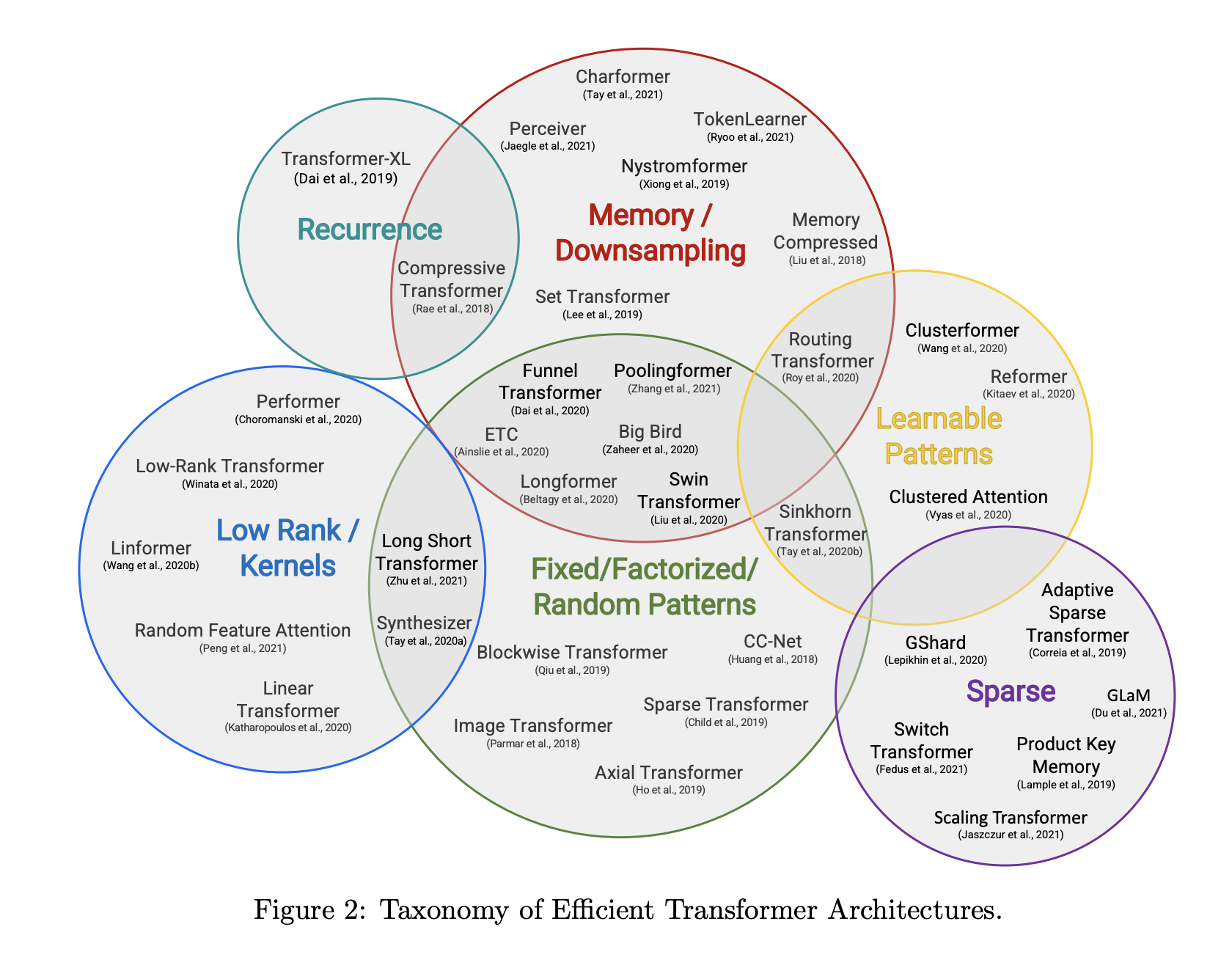
Transformer이 나온지 거의 5년이 지났지만 아직까지 새로운 대체 모델이 나오지 않았고 Transformer의 인기는 식지 않았다. 문제는 Transformer의 time complexity가 quadratic 하다는 것인데, 저자는 이 문제를 해결하려고 했던 논문들을 몇가지 소개했다. 다만 아직도 근본적으로 quadratic 하다는 문제를 해결하지는 못하였다.
Paper Contributions
Introduction to RWKV
저자는 이에 Receptance Weight Key Value (RWKV)라는 새로운 architecture을 제안한다. RWKV는 linear attention mechanism을 하용하며, Transformer의 효율적인 parallelization과 RNN의 효율적인 inference 측면을 동시에 쓸 수 있으므로 computational complexity와 memory complexity를 동시에 잡으면서 모델을 훈련하고 inference를 돌릴 수 있다. 또 scalability issue도 없어서 모델 사이즈를 마음대로 키울 수 있으며(robust scalability), 비슷한 사이즈의 Transformer와 비슷한 성능을 내었다.
RWKV Model
from RNN (LSTM)

저자는 앞서 설명했던 것과 같이 RNN과 LSTM에서도 아이디어를 얻어왔는데, 위와 같은 채널들을 구성해서 각 토큰마다 계산을 해나갔다. 각 cell안에 다음과 같은 수식들이 채널들로써 존재하고, 전 time step의 토큰을 이용해서 다음 토큰을 계산하는데, 이 과정이 해당 모델의 parallelization을 방해한다.
from Transformers and AFT
Transformer가 NLP 분야를 장악했다는 것은 말할 것도 없다. Transformer의 Attention을 계산할 때에는 밑의 식과 같은 방식으로 계산을 진행하게 된다.
Attention은 Q와 K의 dot product를 계산하는 과정에서 나오게 되는데, 이는 행렬의 dot product 연산으로, 모든 토큰들 중 두개씩 잡아서 계산하는 모든 경우의 수를 말한다. 그 식을 다음과 같이 t(0<=t<=seq_len)에 대해 전개할 수 있다.
두 변수 t와 i에 대해 모든 경우의 수의 Q와 K의 dot product를 곱해서 softmax를 씌우는 과정을 한 식에 나타냈다고 할 수 있다. Related Works 부분에서 소개했던 모델 중 하나인 AFT(Attention Free Transformer) 에서는 위의 식을 좀 더 변형해서 사용하고 있다. Attention Free Transformer는 Transformer가 Attention을 계산하는 과정에서 너무나도 큰 Matrix block을 한 번에 곱하기 때문에 계산량이 너무 커 이를 줄이기 위해 고안되었다. 그에 영감을 받아 식을 밑과 같이 변형하여 RWKV에서 사용하고 있다.
의 값은 (seq_len, seq_len) 사이즈의 matrix로, learned pair-wise position bias를 나타낸다. 이 모델 역시 Attention Free 모델로, Attention을 계산하는 과정이 위의 식과 같은 방식으로 이루어진다. 이 Attention 계산은 WKV Cell에서 이루어진다. 모델 전체의 전개도와 함수를 한 번에 지켜보면 좀 더 쉽게 이해할 수 있었다.
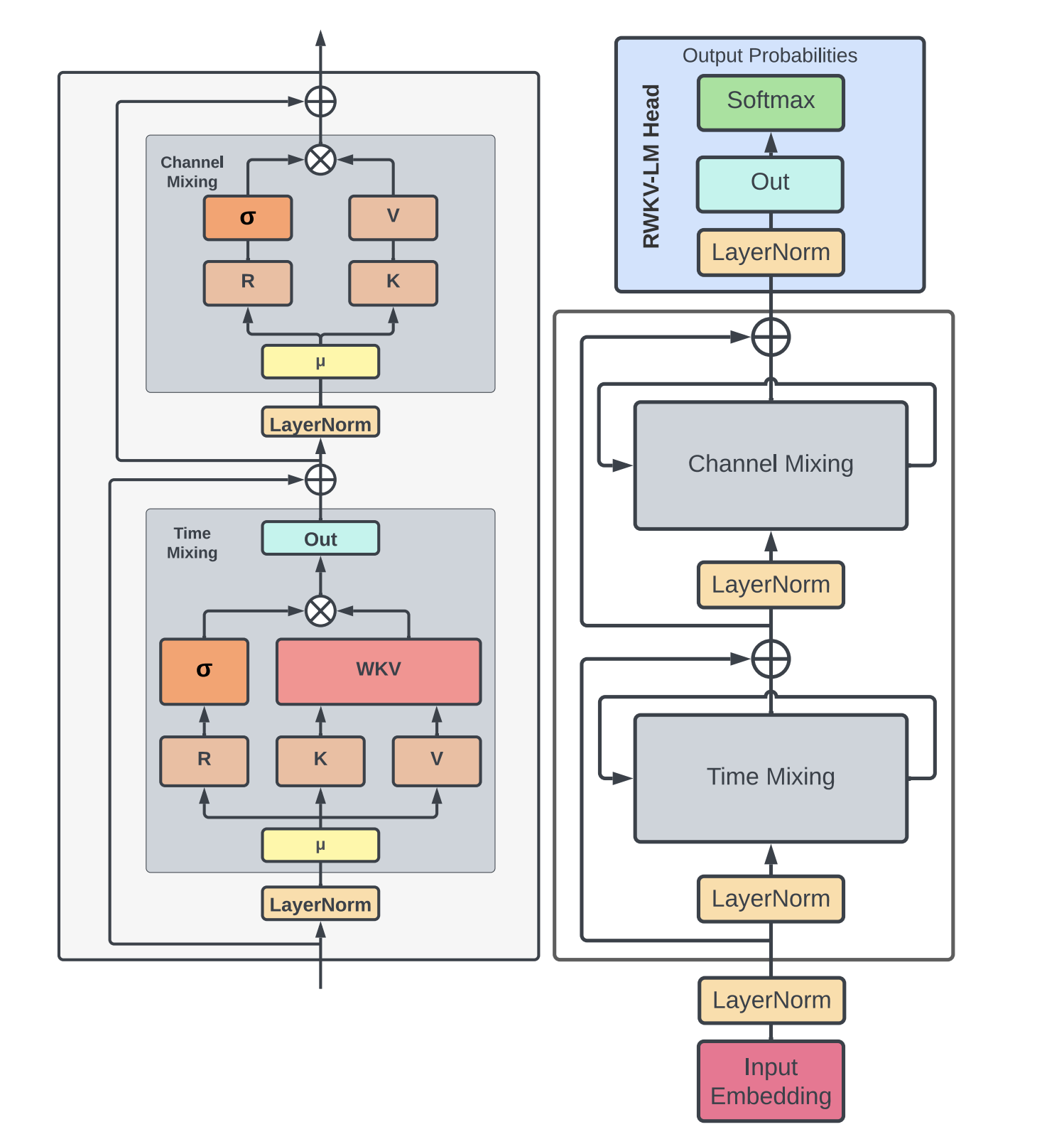
다음은 함수의 전개도이다. 나머지는 모두 linear layer를 뜻하므로 이해하기 어렵지 않은데, \mu와 WKV는 어떻게 연산하는지 잘 이해하기 힘들다. RWKV와 이 둘을 한 번 이해해보자.
Time Mixing
이 논문의 제목인 RWKV는 각각 Receptance, Weight, Key, Value를 의미한다.
-
R: Receptance는 과거의 정보를 어느 정도 수용하는 레이어다. forget gate의 아이디어를 사용하여 전 토큰의 정보를 가져오되 전체가 아니라 어느정도만 가져오고 나머지는 버리는 형식이다. 또한 이 이후 Receptance의 경우에는 Sigmoid를 적용하여 불필요한 과거 정보를 소거한다.
-
W: Weight는 다른 것들과는 다르게 파라미터의 형식이다. 코드에서는 bias=False인 Linear 레이어로 구상되게 되는데 R, K, V를 계산할 때 각각 곱하게 되는 훈련할 수 있는 파라미터이다.
-
K, V: Key와 Value는 Transformer의 Attention에서도 나온다. 다만 여기서는 Q와 dot product를 하지 않는다.
time decay의 경우 (, ) 각 원소들 간의 위치 관계를 얼마나 민감하게 살펴볼건지를 결정한다. 각 파라미터의 경우도 훈련가능한 파라미터로, 학습을 돌리면서 훈련하게 된다. 새로운 정보가 들어올수록 과거의 정보의 영향력이 점점 줄어가는 과정에 매우 중요한 역할을 수행하게 된다.
\mu는 time mix된 결과를 가리킨다. 먼저 time shift라는 변수를 만들어 한 토큰씩 오른쪽으로 민 변수를 만들어낸다. 예를 들어 [4, 59, 10] 이라는 토큰이 주어진다면 한 토큰씩 오른쪽으로 민 변수 time shift는 [0, 4, 59] 가 될 것이다. 코드에서는 nn.ZeroPad((0, 0, 1, -1))를 이용하여 계산한다. 이 이후에는 time_mix_key라는 parameter를 만들어 그 비율만큼 전 토큰과 이후 토큰을 섞어주게 된다. 이에 해당하는 식은 다음과 같다.
위와 같은 식의 형태는 여러 곳에서 사용된 적이 많았는데, 저자는 QRNN에서 아이디어를 얻었다고 언급했다. dynamic average pooling 이라고 명명된 이 식은 forget gate로 사용된다. 즉 LSTM의 forget gate와 비슷하게, 전 토큰의 정보를 어느 정도만 수용하는 것이다.
그렇게 계산된 각각을 각각의 Linear layer에 통과시킨 후 계산을 이어가게 된다.
그 이후에 구조에 나와있는대로 Attention을 계산하기 위해 WKV를 계산하게 된다. 이 과정은 조금 복잡해서 저자에 의하면 코드를 짤 때 numerical stability와 training speed를 올리기 위해서 Custom CUDA Kernel을 직접 제작해서 넣었다고 한다. 다만 이 글에서는 이 점까지는 다루지 않고 파이썬 CPU 연산에서는 계산할 때 어떤 일이 벌어지는지를 알아보려고 한다.
시그마를 제외하고 식을 써보면 어떻게 코드를 짤지가 한눈에 보인다. WKVt를 시그마 대신 WKV{t-1}에 대한 점화식으로 표현해 보면 다음과 같다.
시그마를 풀어보면 위와 같이 나타낼 수 있었으며, 과 의 size는 k_t와 같은 사이즈이다.
그 이후에 와 서로 곱하기 연산을 하게 된다.
FeedForward Layer
Feedforward의 경우에는 비교적 계산과정이 훨씬 쉽다.
Small Init Embedding
Transformer를 학습시킬 때 embedding matrix가 느리게 바뀌는 문제가 있었는데 이는 모델 초반에 noisy한 embedding layer을 달고서 학습이 진행되므로 문제가 될 수 있다. 이 문제점을 해결하기 위해 embedding layer를 작은 숫자들로 initialize한 후에 추가적으로 LayerNorm layer을 붙여서 해결했다. 이를 통해 훈련 과정이 좀 더 빨라지고 안정적으로 진행됐으며, convergence도 더 잘 진행되었다. 결국 LayerNorm 이후에 있는 레이어들이 방향성을 잘 찾아 학습되었다.
Evaluations
우리는 새로운 아키텍쳐인 RWKV 모델에게 몇가지 질문을 해야한다.
N^2의 트랜스포머 구조와 비교했을 때 같은 파라미터 수와 같은 훈련 토큰 개수에 대해 성능이 비빌만 한가?
과연 트랜스포머와 비교해서 성능이 비빌만 한가?
만약 파라미터 수를 늘리면 훈련때 loss가 줄어드는게 보인다면, 트랜스포머가 효율적으로 할 수 없는 작업들을 처리할 수 있나?
밑의 자료를 보면 RWKV는 computationally efficient 하다고 할 수 있다. 6개의 벤치마크에서 모두 트랜스포머 아키텍쳐를 사용한 모델들과 비교해서 성능이 비슷하게 나왔다.
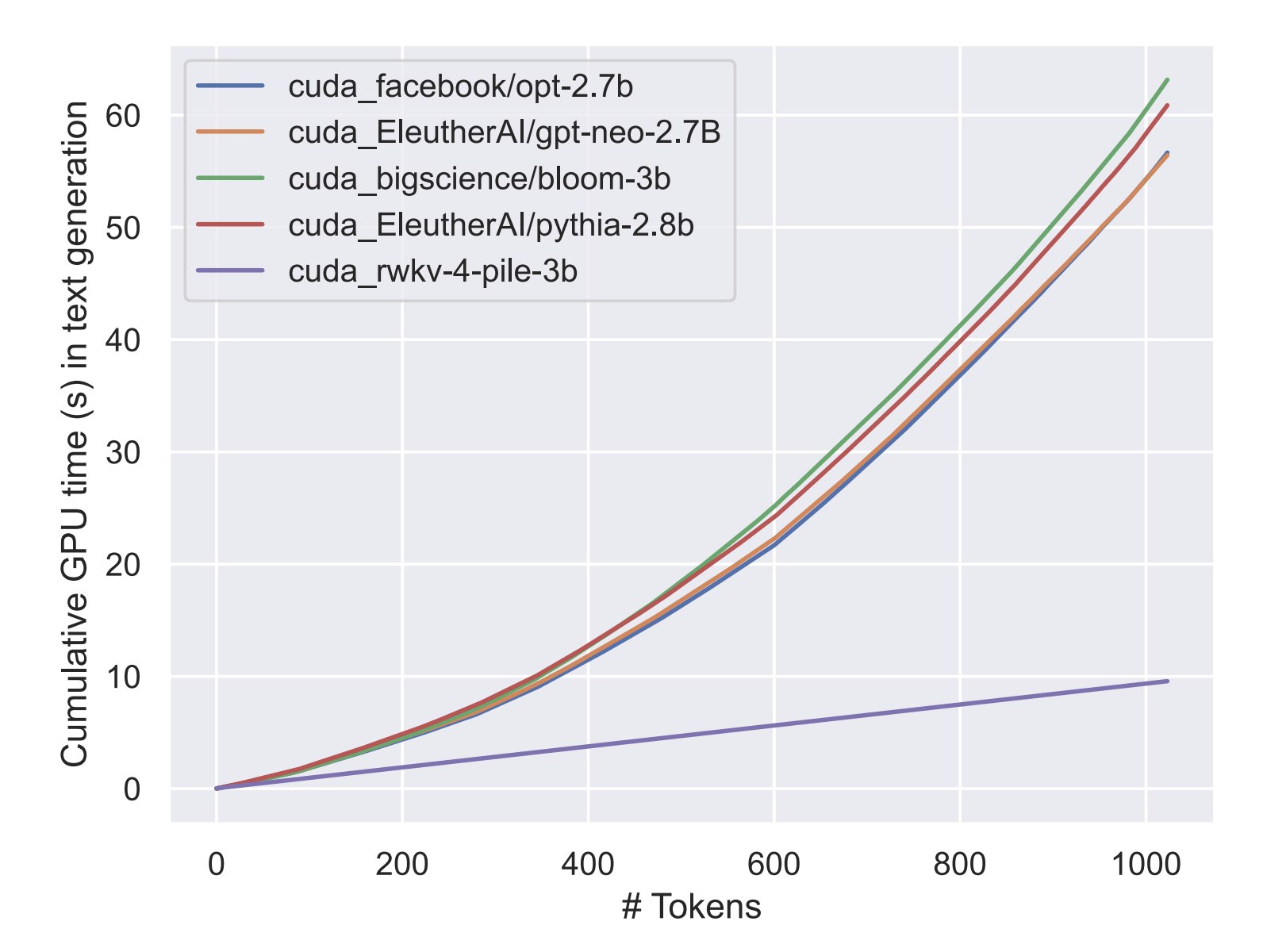
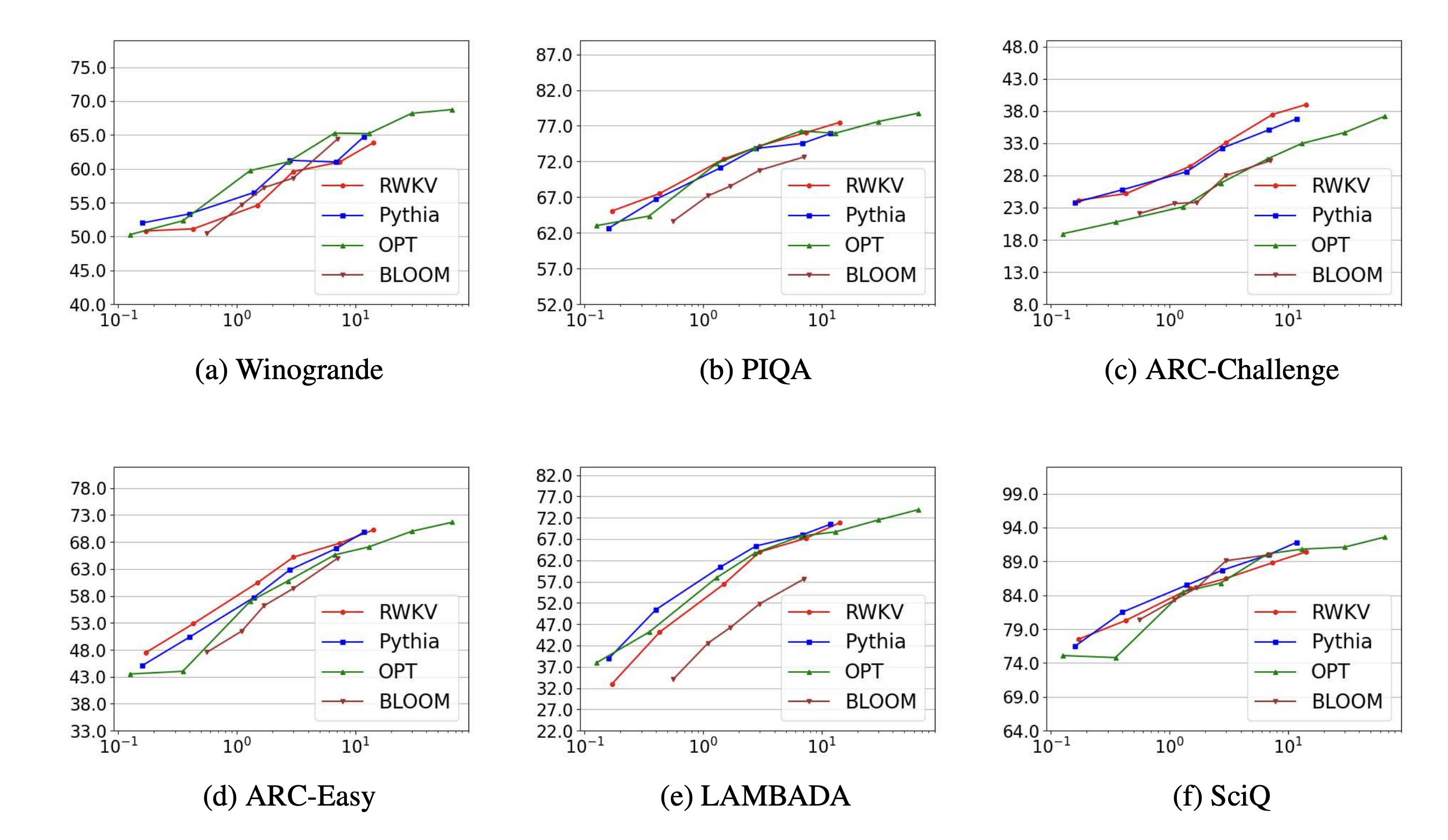
Summary
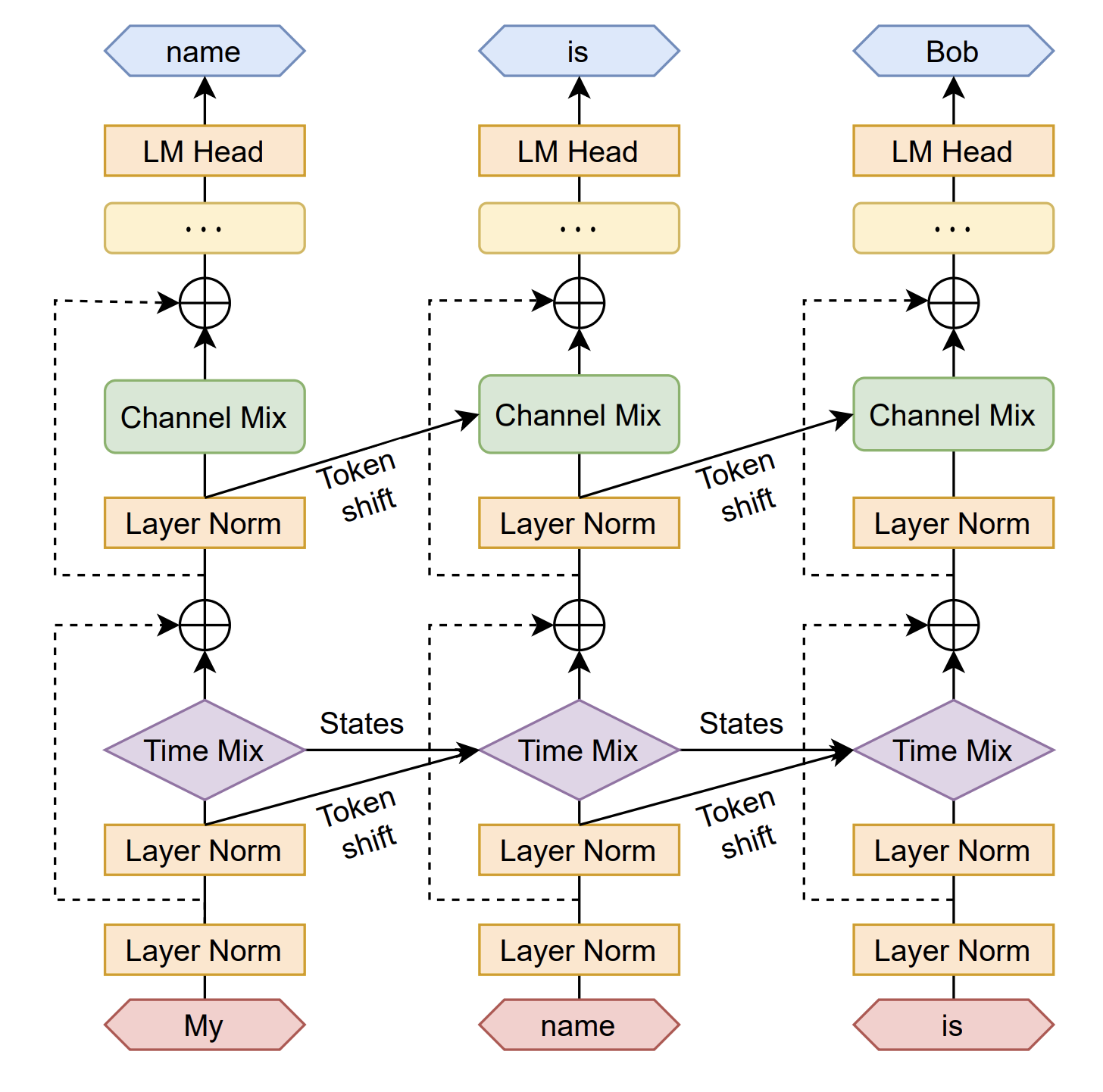
위와 같은 과정을 통해 계산을 하게 되면 RNN과 Attention mechanism을 쓰면서도 parallel하게 확장을 할 수 있게 되므로 Transformer와 비슷한 성질을 갖게 된다.
Limitations
RWKV가 꽤 잘 작동하지만 여러가지 한계점이 있다.

