문제 정의

업데이트 버전을 적용하기 전에 업데이터의 컨텐츠와 방식에 대한 전반적인 내용이 변경될 때 유저의 반응을 테스트

소스코드 및 데이터 : GitHub

AB test

다양한 웹페이지, 어플리케이션, 게임, 마케팅 등 서로 다른 2개의 상황에서의 반응률을 비교하여 어떤 상황이 더 효과적인지 판단하는 방법론이다.
A는 기존 B는 변경 사항을 비교하거나 혹은 A의 버튼 색, 카피 등과 B의 버튼 색, 카피 등을 비교한다.

데이터 확인

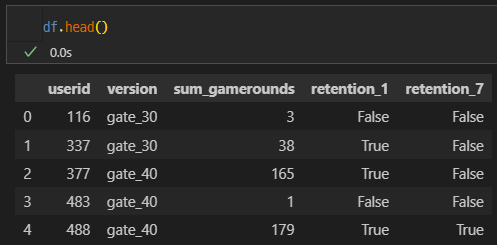
• 데이터 features

user_id	version	sum_gamerounds	retention_1	retention_7
사용자 ID	버젼	총 플레이 횟수	1일 이후 재방문	7일 이후 재방문

데이터 EDA & 전처리

기본 정보

version
버전은 두 가지가 있다.

df['version'].unique()
---
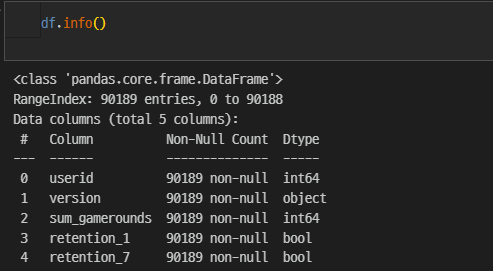
array(['gate_30', 'gate_40'], dtype=object)

data info

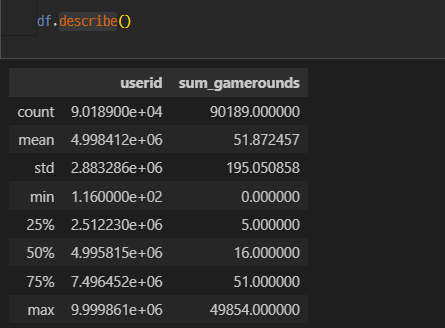
data describe
sum_gamerounds는 평균에 비해서 최대값이 크다.
데이터를 좀 더 확인해보고 최대값을 가지는 것이 이상치인지 확인을 해야한다.

밀도 그래프로 값들의 분포를 확인해보자.
대부분 0에 가까운 값(평균값이 52정도)에 몰려있는 것을 확인할 수 있다.
최대값은 이상치로 보는 것이 합당한 것으로 보인다.(이상치는 도메인 지식 기반으로 처리를 진행하는 것이 합당하다)

plt.figure(figsize=(12, 8))
sns.distplot(df['sum_gamerounds'])
plt.show()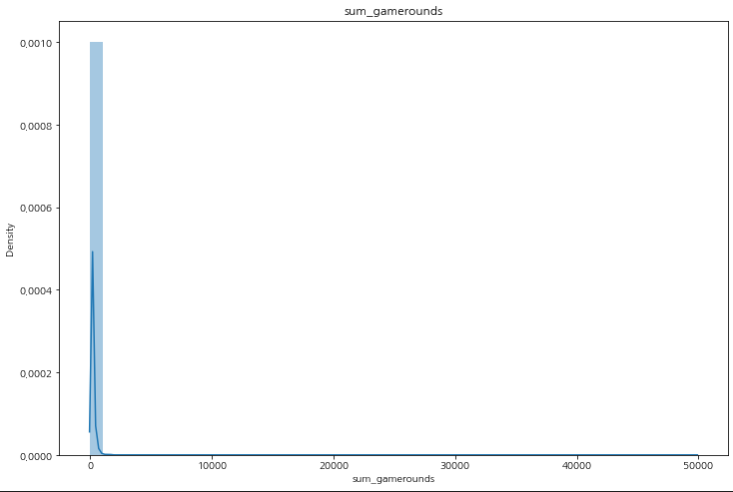

2,000이 넘어가는 데이터를 확인해보면 아래와 같은데,
최대값도 보이는 것으로 보아 이상치라고 판단하는 것이 더 합당하다.

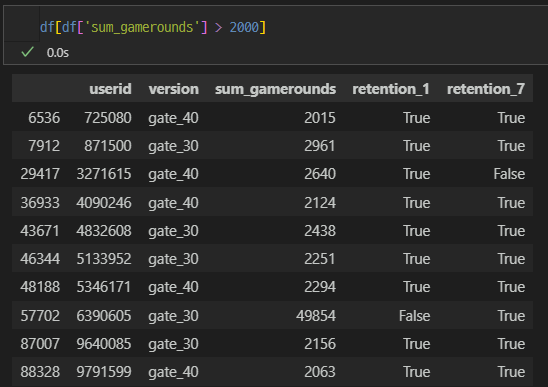
이상치라고 판단이 된다면 1,000이하의 값들로 다시 통계값들을 확인해보자.

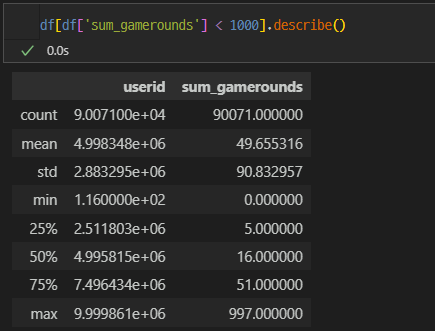
데이터 치우침
sum_gamerounds는 데이터의 쏠림 현상이 있다.

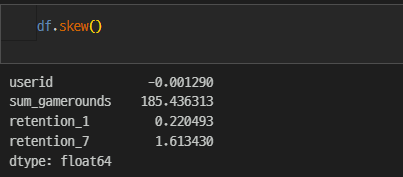
결측치
결측치는 없다.

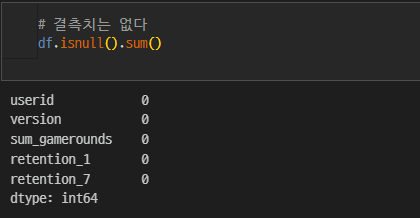
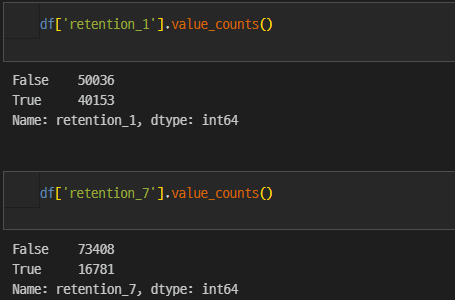
retention
retention_7은 클래스 불균형이 존재한다.

version data 분포

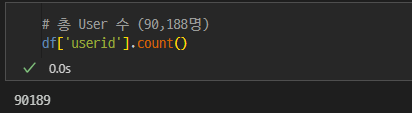
AB test를 진행한 총 유저의 수는 약 9만명으로 확인된다.

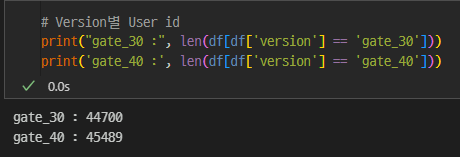
그리고 버전별 유저는 약 50:50으로 균등하게 나뉘어져 있다.
버전에 대한 유저수도 균등하게 나눠져 있다는 것이 확인된다.

그렇다면 버전별 플레이 횟수에 대한 분포는 어떤지 확인해보자.

sns.kdeplot(df[df['version']=='gate_30']['sum_gamerounds'], shade=True, label='gate_30')
sns.kdeplot(df[df['version']=='gate_40']['sum_gamerounds'], shade=True, label='gate_40')
plt.gcf().set_size_inches(25, 5)
plt.legend()
plt.xlim(-100, 100)
plt.show()

버전별로 유저 플레이 횟수에 대한 큰 차이는 보이지 않지만 gate 30이 조금 더 높은 것이 확인 된다.

retention_1에 대한 버전별 차이를 확인하고

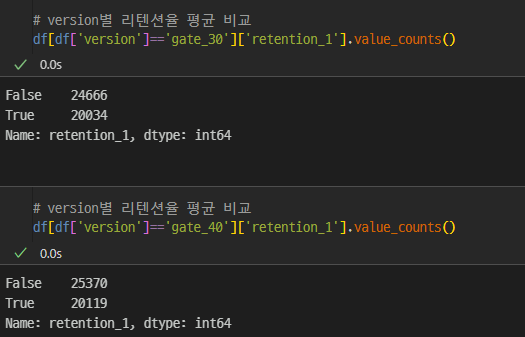
retention_7에 대한 버전별 차이를 확인하였을 때,

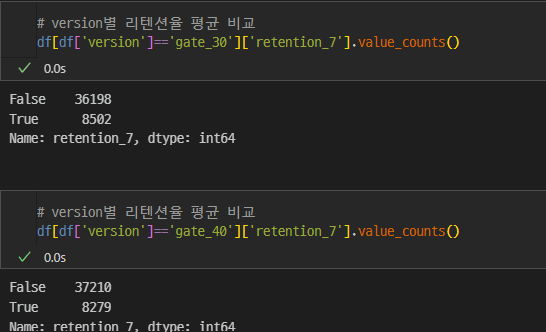
gate 30이 조금 더 접속률이 높은 것을 확인할 수 있다.

retention 전처리

bool 타입의 retention을 0과 1로 대체.

# retention 값 변경
df['retention_1'] = np.where(df['retention_1'] == True, 1, 0)
df['retention_7'] = np.where(df['retention_7'] == True, 1, 0)

변수 확인

버전별 연속형 변수 sum_gamerounds와 범주형 변수 retention가 있다.

연속형 변수는 평균값으로 범주형 변수는 반응률(버전별 접속률)로 확인을 진행한다.

# 연속형 변수는 평균, 범주형 변수는 반응률
df.groupby('version')[['sum_gamerounds', 'retention_1', 'retention_7']].agg(['mean', 'count', 'sum'])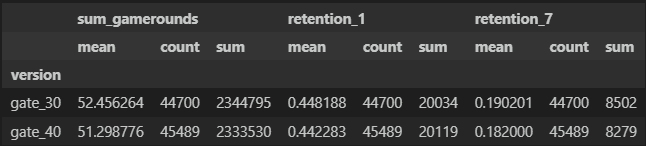

인덱스 정리 및 멀티 인덱스로 되어있는 컬럼을 정리한다.

# 연속형 변수는 평균, 범주형 변수는 반응률, reset_index로 multi index를 제거
df_pivot = pd.DataFrame(df.groupby('version')[['sum_gamerounds', 'retention_1', 'retention_7']].agg(['mean', 'count', 'sum']).reset_index())

# column 정리
df_pivot.columns = ['version', 'sum_gamerounds_mean', 'sum_gamerounds_count', 'sum_gamerounds_sum',
                    'retention_1_mean', 'retention_1_count', 'retention_1_sum', 
                    'retention_7_mean', 'retention_7_count', 'retention_7_sum']
                    
df_pivot = df_pivot[['version', 'sum_gamerounds_mean', 'retention_1_count', 'retention_1_sum', 'retention_7_count', 'retention_7_sum']]

# 반응률 계산
df_pivot['retention_1_ratio'] = df_pivot['retention_1_sum'] / df_pivot['retention_1_count']
df_pivot['retention_7_ratio'] = df_pivot['retention_7_sum'] / df_pivot['retention_7_count']

반응률

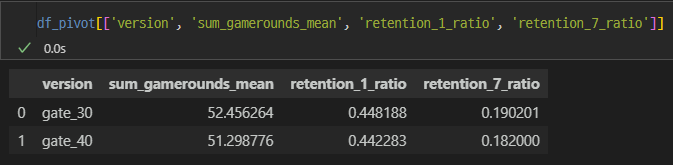
version 차이

T/Chi2 - test

연속형 변수(sum_gamerounds)는 t-test로 범주형 변수(retention)은 Chi2-test로 진행한다.

T - test

참조 : 독립 표본 t 검정
버전 2개의 등분산성 확인
p value가 0.05보다 작기에 버전 간의 플레이 횟수에 대한 분산은 다르다는 것이 확인 된다.

tstat, pvalue = stats.bartlett(df[df['version'] == 'gate_30']['sum_gamerounds'], df[df['version'] == 'gate_40']['sum_gamerounds'])
print("P-value:", round(pvalue,4))
>
P-value: 0.0

독립 표본 t 검정
tstat는 양수로 버전 30의 데이터들의 평균이 더 크지만,
p value가 0.05 이상으로 버전 두 개의 평균 수준은 '같다'라고 할 수 있다.

tstat, pvalue = stats.ttest_ind(df[df.version == 'gate_30'].sum_gamerounds, df[df.version == 'gate_40'].sum_gamerounds, equal_var=False)
print('tstat: ', tstat)
print("P-value:", round(pvalue,3))
>
tstat:  0.8854374331270672
P-value: 0.376

Chi2-test

참조 : 카이제곱 검정
카이제곱 검정을 통해 두 변주형 변수가 서로 독립적인지 확인해보자.

retention 1과 7의 반응률에 대한 비교를 진행한다.

retention 1

retention에 반응한 수와 아닌 수에 대한 데이터를 생성한다.

# 필요한 Data만 추출
df_pivot_1 = df_pivot[['version', 'retention_1_count', 'retention_1_sum']]

# 반응한 고객과 반응하지 않은 고객에 대한 관찰 빈도가 필요함
df_pivot_1['retention_1_no'] = df_pivot_1['retention_1_count'] - df_pivot_1['retention_1_sum']
df_pivot_1 = df_pivot_1[['retention_1_sum', 'retention_1_no']]
df_pivot_1.columns = ['yes', 'no']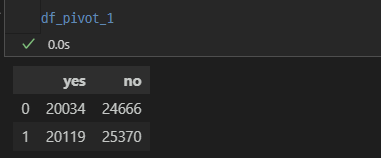

검정
p-value가 0.05 이상인 것으로 보아, 서로 독립적이지 않은 즉, retention의 반응률에는 차이가 없는 것으로 보인다.

statistics, p_value, dof, expected = stats.chi2_contingency(df_pivot_1)

print('p-value :', p_value)
>
p-value : 0.07550476210309086

retention 7

retention에 반응한 수와 아닌 수에 대한 데이터를 생성한다.

# 필요한 Data만 추출
df_pivot_2 = df_pivot[['version', 'retention_7_count', 'retention_7_sum']]

# 반응한 고객과 반응하지 않은 고객에 대한 관찰 빈도가 필요함
df_pivot_2['retention_7_no'] = df_pivot_2['retention_7_count'] - df_pivot_2['retention_7_sum']
df_pivot_2 = df_pivot_2[['retention_7_sum', 'retention_7_no']]
df_pivot_2.columns = ['yes', 'no']
df_pivot_2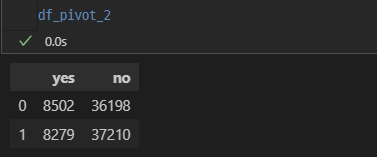

검정
p-value가 0.05 미만인 것으로 보아, 서로 독립적이므로 retention의 반응률에는 차이가 있는 것으로 보인다.

statistics, p_value, dof, expected = stats.chi2_contingency(df_pivot_2)
print('p-value :', p_value)
>
p-value : 0.0016005742679058301

결론

버전별 차이를 확인해보자.

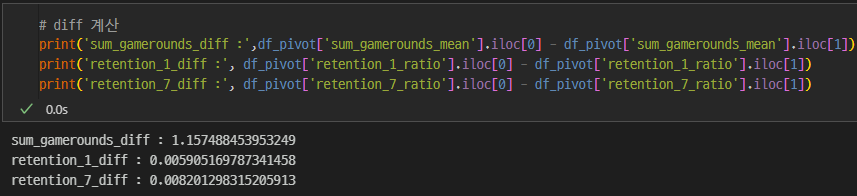
# diff 계산 Gate30 - Gate40
print('sum_gamerounds_diff :',df_pivot['sum_gamerounds_mean'].iloc[0] - df_pivot['sum_gamerounds_mean'].iloc[1])
print('retention_1_diff :', df_pivot['retention_1_ratio'].iloc[0] - df_pivot['retention_1_ratio'].iloc[1])
print('retention_7_diff :', df_pivot['retention_7_ratio'].iloc[0] - df_pivot['retention_7_ratio'].iloc[1])

>
sum_gamerounds_diff : 1.157488453953249
retention_1_diff : 0.005905169787341458
retention_7_diff : 0.008201298315205913

• Gate30이 Gate40 대비 +0.04 더 많은 게임플레이횟수를 보였으나 우연에의해 차이가 발생했을 확률이 높다
• Gate30이 Gate40 대비 +0.005%p 더 많은 설치 후 1일 이내 리텐션율을 보였고, 유의성이 없다
• Gate30이 Gate40 대비 +0.008%p 더 많은 설치 후 7일 이내 리텐션율을 보였고, 신뢰수준 98%(p-value가 0.0016) 이상으로 유의성이 있다.

기대 효과

도메인 지식 하에 통계가 유의미하다면, version 30 선정을 하는 것이 더 유의미하다.
버전을 업데이트 확정 및 진행