최소 신장 트리란?
최소 신장 트리를 알아보기 전에 신장 트리를 알아보자
신장트리 : 어떤 그래프의 부분 그래프이면서 동시에 모든 정점을 포함하는 트리를 이르는 말
정점이 V개일 때 간선은 V-1개이며 트리이므로 사이클이 생겨서는 안된다는 특징이 있다.
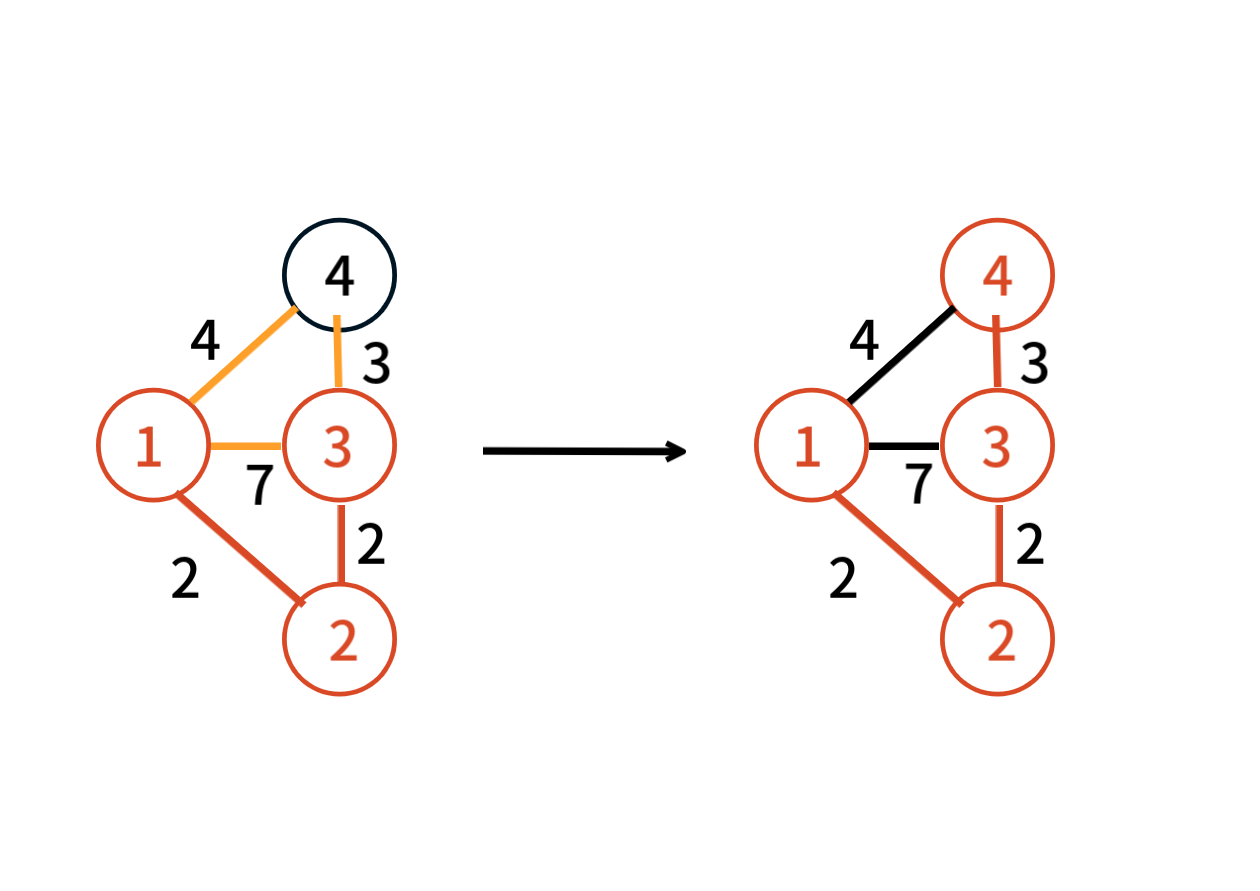
최소 신장 트리는 신장 트리 중에서 간선의 합이 최소인 트리를 말한다.
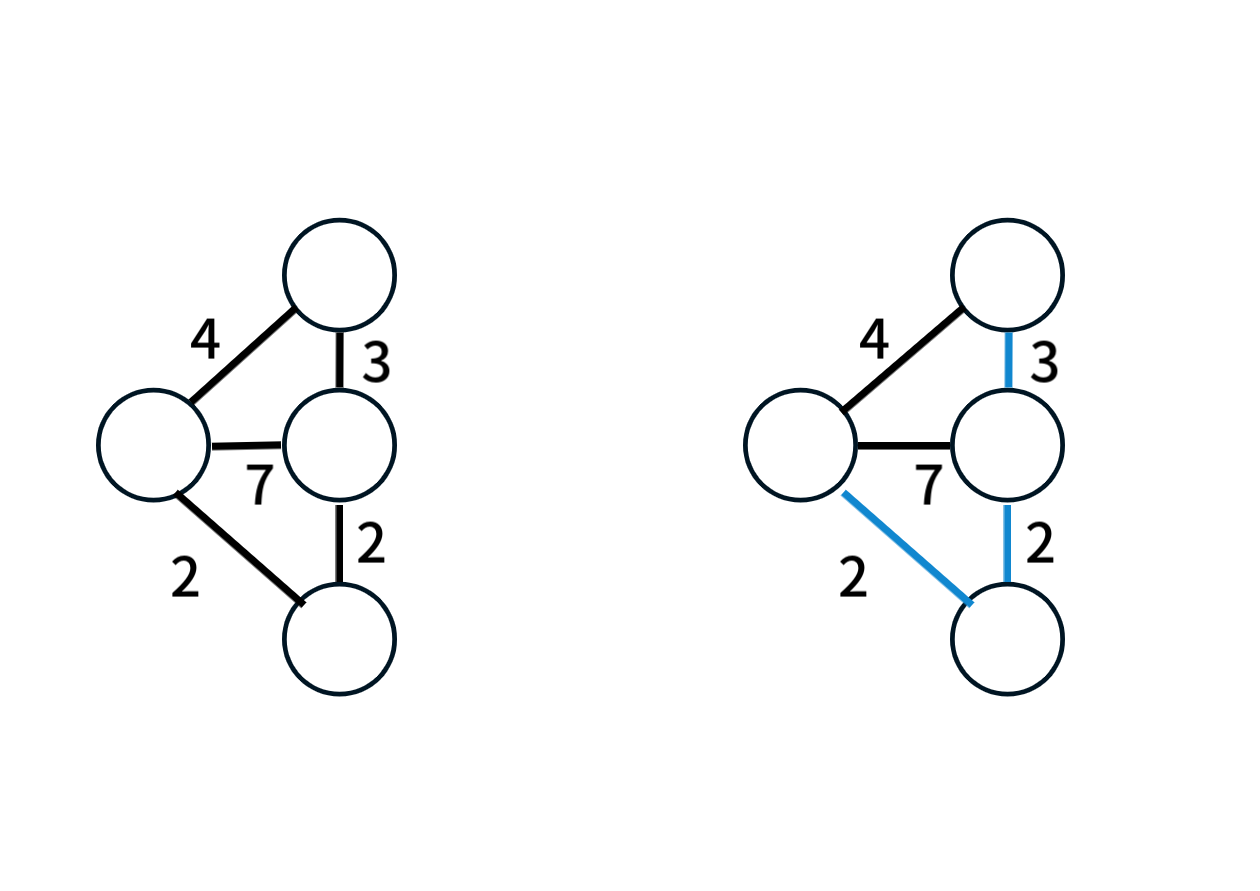
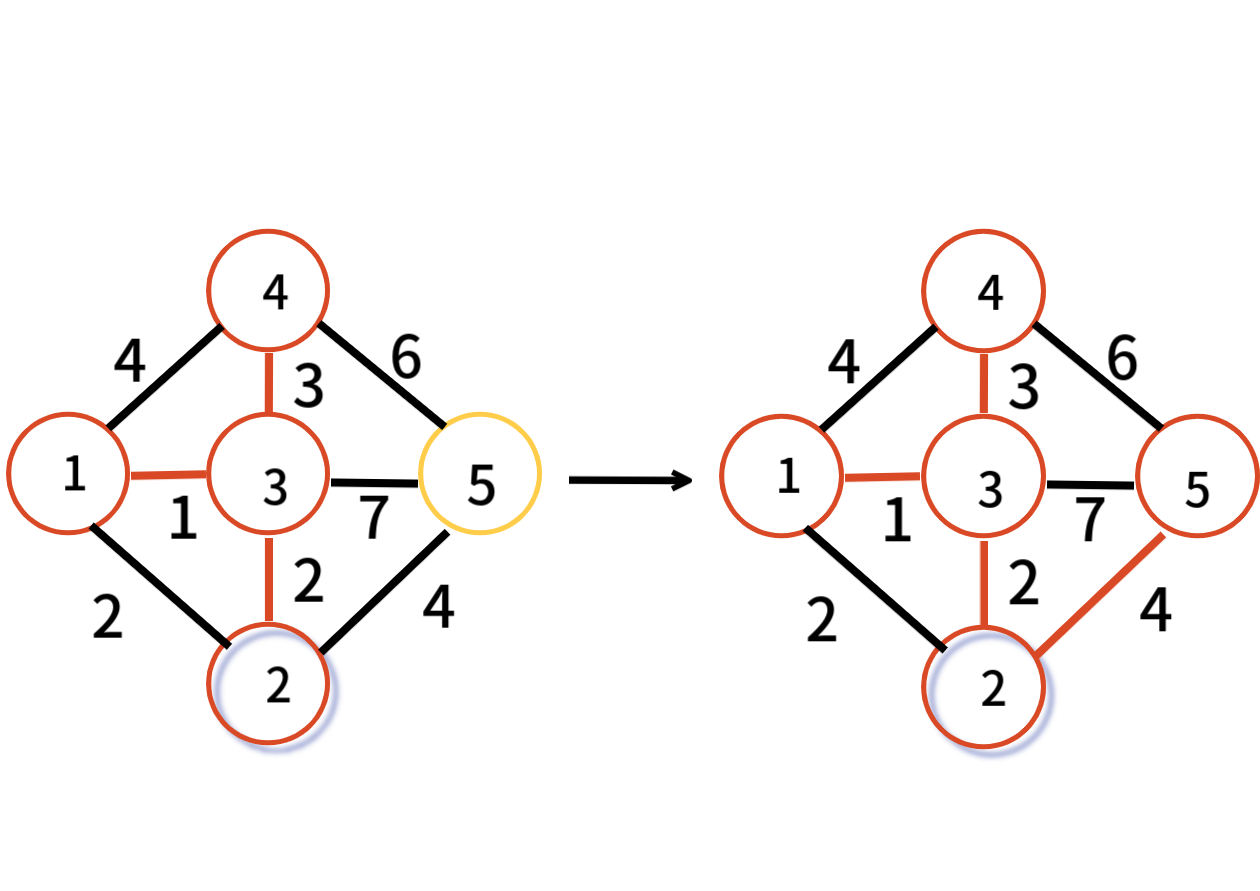
오른쪽 트리는 왼쪽 그래프의 최소 신장 트리이다. (간선의 합 7)
그럼 이제 최소 신장 트리를 어떻게 구현할 수 있는지 알아보자.
최소 신장 트리는 두가지 방법으로 구현할 수 있다.
1. 프림 알고리즘
프림 알고리즘은 간단히 말하면 한 정점에서 시작해 확장해나가는 알고리즘이다.
과정을 먼저 살펴보자.
1-1 프림 알고리즘 과정
- 임의의 정점을 선택해 최소 신장 트리에 추가한다
- 최소 신장 트리에 포함된 정점과 포함되지 않은 정점을 연결하는 간선 중 가중치가 가장 작은 것을 최소 신장 트리에 추가
- 최소 신장 트리에 V-1개의 간선이 추가될 때 까지 2번을 반복한다
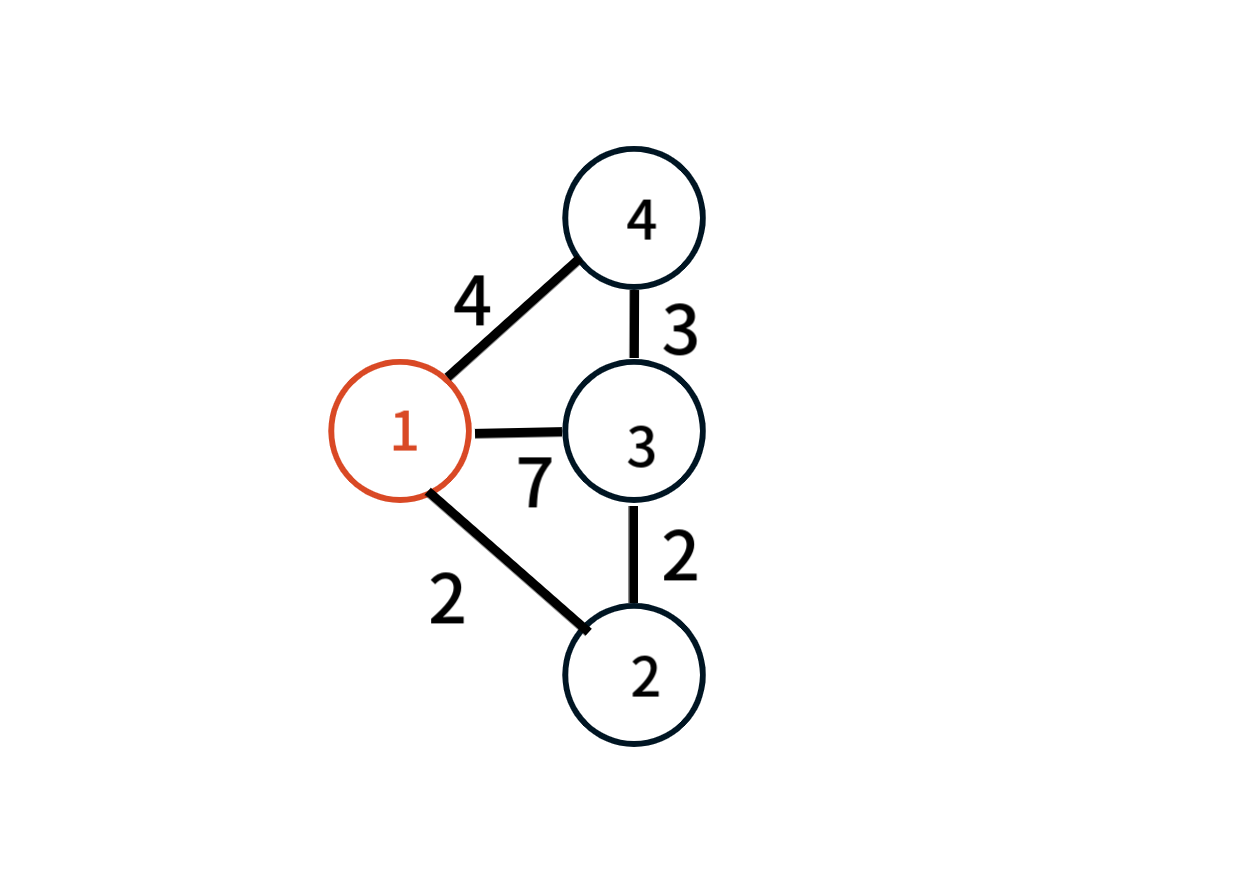임의의 정점으로 1번 정점을 선택한고 최소 신장 트리에 포함시킨다
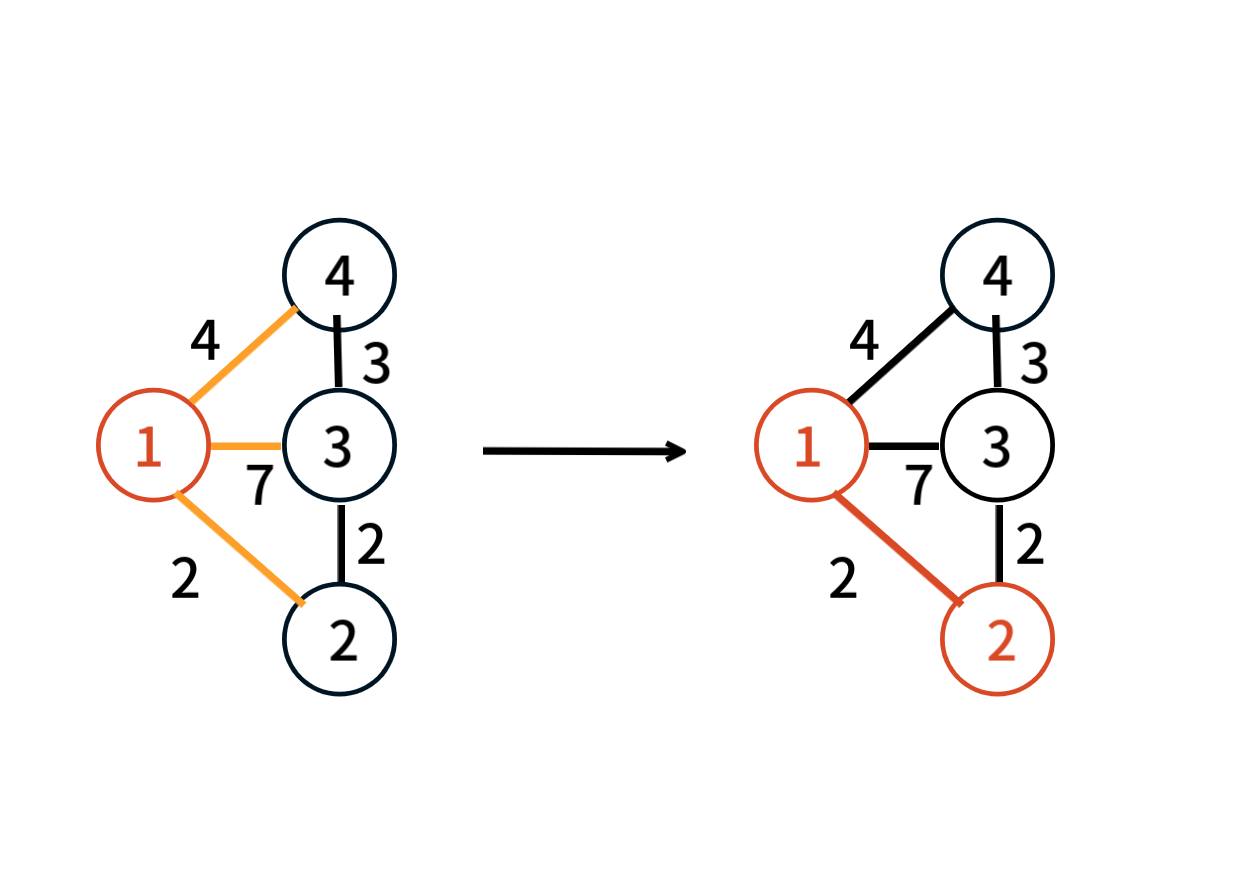최소 신장 트리에 포함된 1번 정점과 인접한 정점을 연결하는 간선 중 가중치가 가장 작은 것을 최소 신장 트리에 추가한다
반복한다
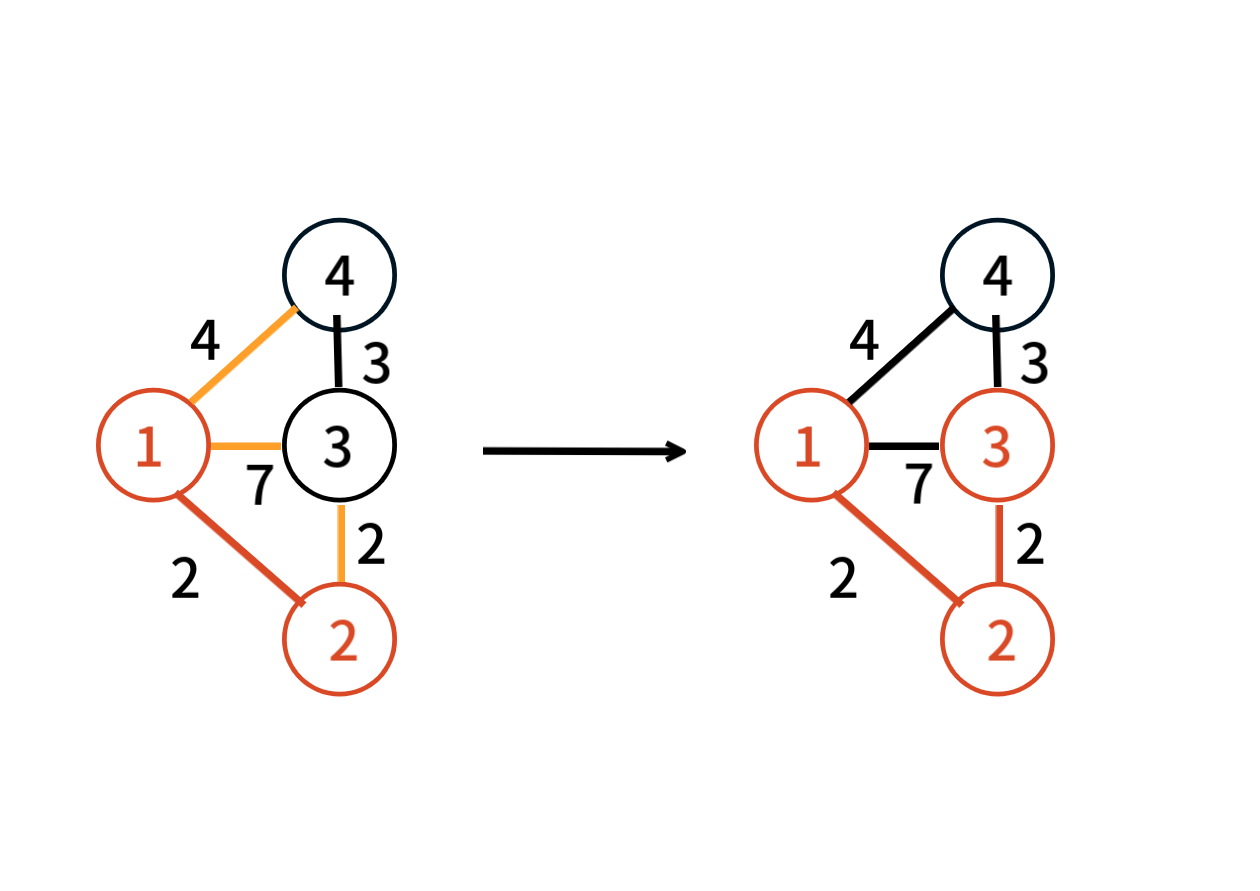
V-1개의 간선이 선택되면 알고리즘이 끝나게 된다
항상 최소가 되는 간선을 선택해야하므로 우선순위 큐를 사용하여 구현할 수 있다.
1-2 프림 알고리즘 구현 코드
#include <bits/stdc++.h>
using namespace std;
// <가중치,정점 번호>
vector <pair<int,int>> adj[10002];
// <가중치,정점1,정점2>
priority_queue <tuple<int,int,int>,
vector<tuple<int,int,int>>,
greater<tuple<int,int,int>> > pq;
//정점이 최소 신장 트리에 속해있는지를 나타내는 배열
bool chk[10002];
int main()
{
int v,e;
cin >> v >> e;
int a,b,value;
for(int i=1; i<=e; i++)
{
cin >> a >> b >> value;
adj[a].push_back({value,b});
adj[b].push_back({value,a});
}
//임의 정점을 최소 신장 트리에 포함한다(여기선 1)
chk[1] = 1;
for(auto nxt : adj[1])
{
pq.push({nxt.first,1,nxt.second});
}
int cnt=0;
int value_sum=0;
while(cnt <v-1) //v-1개의 간선이 포함되도록
{
int a,b,cost;
//cost,a,b에 각각 가중치가 가장 작은 간선의 비용,시작정점,끝정점을 대입
tie(cost,a,b) = pq.top();
pq.pop();
if(chk[b])
continue;
chk[b]=1;
cnt++;
value_sum+=cost;
for(auto nxt: adj[b])
{
if(!chk[nxt.second])
pq.push({nxt.first,b,nxt.second});
}
}
cout << value_sum;
}위에서 본 과정을 이해했다면 구현은 어렵지 않지만 STL이 익숙하지 않다면 어려울 수 있다.
우선순위 큐에 간선의 비용,시작 정점,끝 정점을 담기 위해 tuple을 사용한다. pq.push({nxt.first,b,nxt.second})는 우선순위 큐에 간선의 비용,시작 정점,끝 정점 순으로 넣는 것이고 가중치가 가장 작은 간선이 top에 오게 되는 것이다.
1-3 프림 알고리즘 시간 복잡도
우선순위 큐의 삽입, 삭제의 시간복잡도는 O(lgE)이고 각 간선은 우선순위 큐에 최대 1번 삽입, 삭제 !
되므로 프림 알고리즘의 시간 복잡도는 O(ElgE)이다.
*참고: 이 코드는 백준 1197번 최소 스패닝 트리를 프림 알고리즘으로 구현한 것이다.
2. 크루스칼 알고리즘
크루스칼 알고리즘은 가중치가 작은 간선을 선택해나가며 최소 신장 트리를 만든다.
2-1 크루스칼 알고리즘 과정
- 간선을 가중치가 작은 순으로 정렬한다.
- 정렬된 간선 순으로 간선을 선택한다. 선택된 간선의 두 정점 u,v가 같은 그룹이면 넘어가고 다른 그룹이면 같은 그룹으로 만들고 선택한 간선을 최소 신장 트리에 추가한다.
- 최소 신장 트리에 포함되 간선이 V-1개 일 때까지 2,3번을 반복한다.
각 정점의 그룹을 각각 다르게 설정한다.
간선이 가중치가 작은 순으로 정렬되있다고 하자.
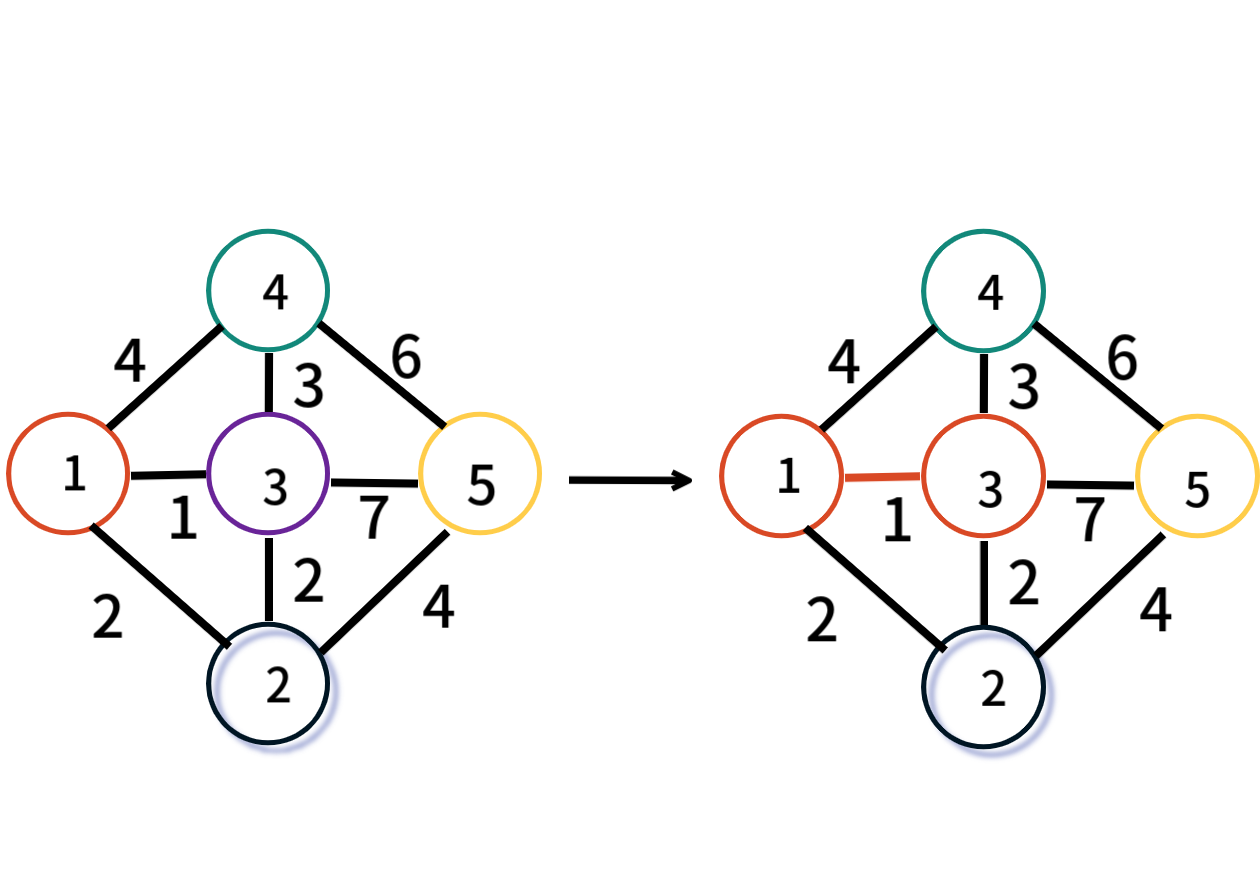
1번 정점과 3번 정점을 잇는 가중치 1의 간선이 선택된다.
1번과 3번의 그룹이 다르니 같은 그룹으로 만들고 최소 신장 트리에 추가한다.
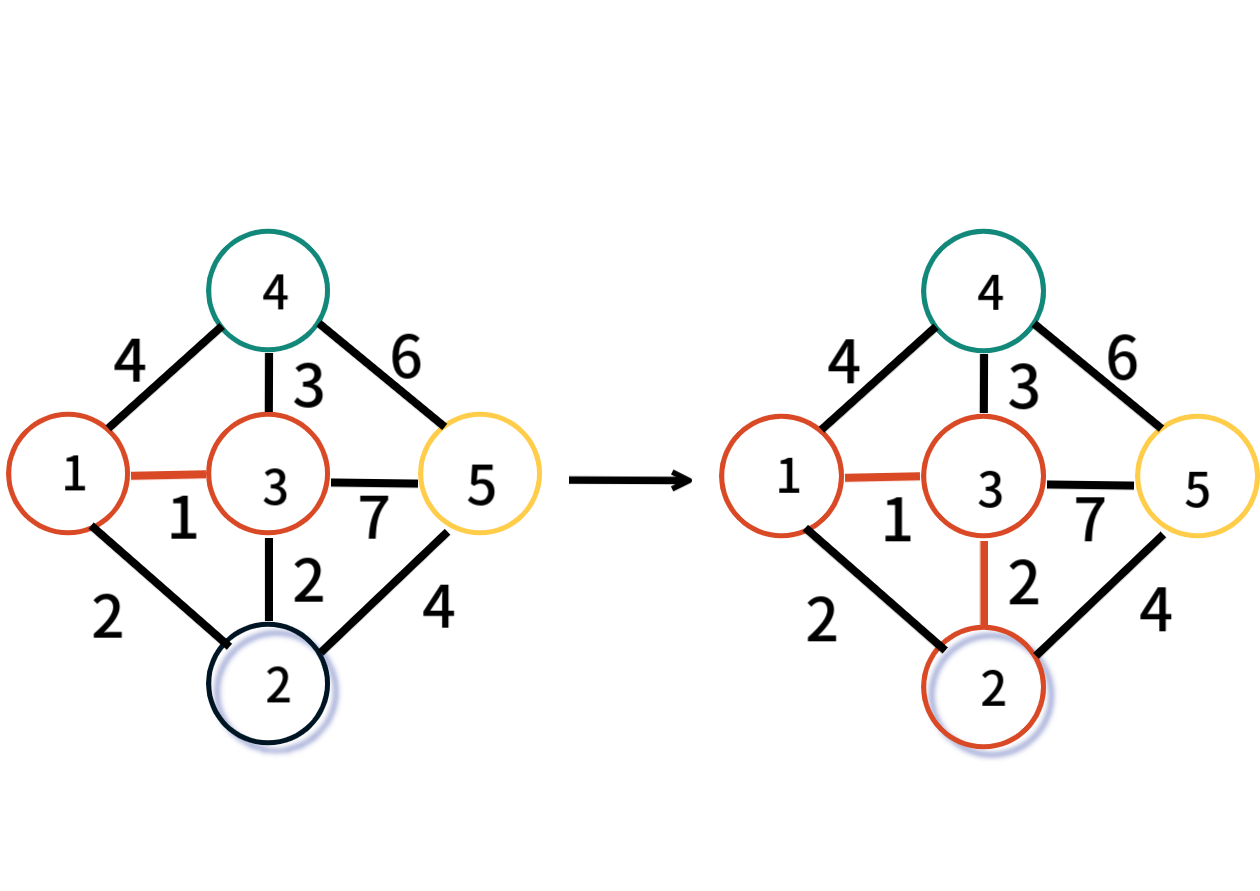다음으로는 2번 정점과 3번 정점을 잇는 가중치 2의 간선이 선택되고 2번과 3번의 그룹이 다르니 같은 그룹으로 만들고 최소 신장 트리에 추가한다.
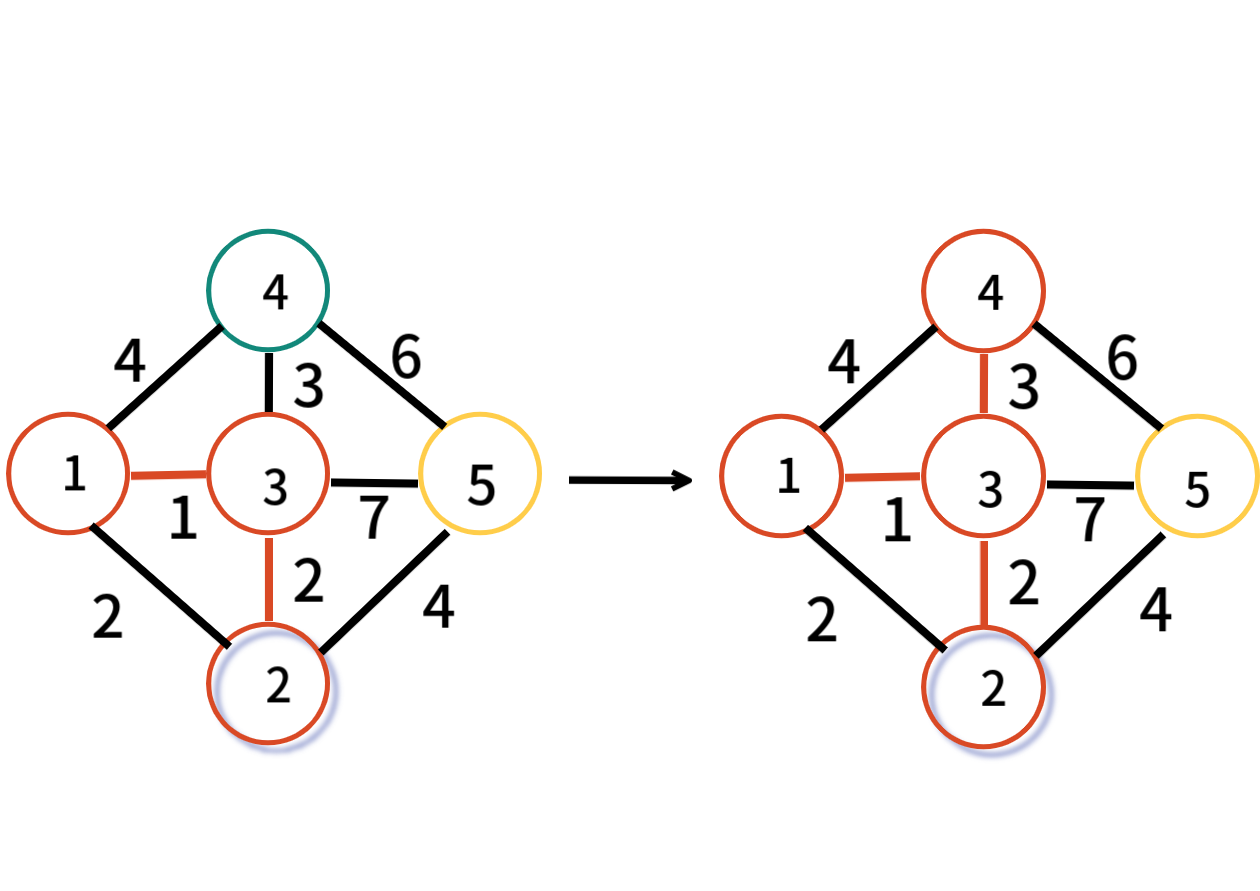1번 정점과 2번 정점을 잇는 가중치 2의 간선이 선택되야 하는데 1번과 2번은 같은 그룹이므로 간선 선택시 사이클이 생긴다. 따라서 선택하지 않는다.
다음 순서인 3번과 4번을 잇는 가중치 3의 간선이 선택되고 3번과 4번의 그룹이 다르니 같은 그룹으로 만들고 최소 신장 트리에 추가한다.
2번과 5번을 잇는 가중치 4의 간선이 선택되고 2번과 5번의 그룹이 다르니 같은 그룹으로 만들고 최소 신장 트리에 추가한다.
V-1개의 간선을 선택했으니 알고리즘이 종료된다.
2-2 크루스칼 알고리즘 구현 코드
#include <bits/stdc++.h>
using namespace std;
vector <tuple<int,int,int>> adj;
int v,e;
int parent[10002];
//자신이 어느 그룹에 속해있는지를 알려주는 find함수
int find(int x)
{
if(parent[x] == x)
return x;
return parent[x] = find(parent[x]);
}
//두 정점의 그룹이 다르면 같게 만들고 false를 리턴하고 같으면 true를 리턴한다
bool Union(int x, int y)
{
x = find(x);
y = find(y);
if(x==y)
return true;
if(x < y)
{parent[y] = x;}
else
{parent[x] = y;}
return false;
}
int main()
{
cin >> v >> e;
//각 정점의 그룹을 다르게 설정한다
for(int i=1; i<=v; i++)
parent[i] = i;
int a,b,value;
for(int i=1; i<=e; i++)
{
cin >> a >> b >> value;
adj.push_back({value,a,b});
}
//간선의 가중치를 기준으로 오름차순 정렬
sort(adj.begin(),adj.end());
int sum=0;
int cnt=0;
for(auto nxt : adj)
{
if(cnt == v-1)
break;
int a,b,cost;
tie(cost,a,b) = nxt;
//두 정점의 그룹이 같으면 건너뛴다
if(Union(a,b))
continue;
sum+=cost;
}
cout << sum;
}크루스칼 알고리즘을 구현 하기 위해서는 Union-find 알고리즘을 이해해야한다. 여기서 다루기엔 내용이 길어지니 간단히 기능만 설명하겠다..!
parent배열은 자신이 어느 그룹에 속해있는지를 나타내는 배열이다. 자신의 그룹을 자신의 정점 번호로 초기화 한 뒤 알고리즘을 실행한다.
int find(int x)
{
if(parent[x] == x)
return x;
return parent[x] = find(parent[x]);
}find함수는 자신이 속한 그룹을 리턴해주는 함수이다.
bool Union(int x, int y)
{
x = find(x);
y = find(y);
if(x==y)
return true;
if(x < y)
{parent[y] = x;}
else
{parent[x] = y;}
return false;
}Union함수는 두개의 정점 각각의 그룹을 find함수를 통해 찾고 그룹이 같으면 true를 리턴해서 건너뛰게 한다.
그룹이 다르면 두 그룹을 같게 만든다. 위에 그림 과정에서 3의 그룹을 1의 그룹과 같게 했는데 parent[3]=1; 을 한것과 같다.
간선이 V-1개 추가될때까지 반복문을 돌리고 빠져나온다.
2-3 크루스칼 알고리즘 시간복잡도
Union-find는 상수의 시간복잡도를 갖는다. 또한 모든 간선을 정렬하는 알고리즘의 시간 복잡도는 O(ElgE)이기 때문에 O(ElgE)이다.
*참고: 이 코드는 백준 1197번 최소 스패닝 트리를 크루스칼 알고리즘으로 구현한 것이다.
최소 신장 트리 관련 문제
백준 16398 행성 연결 / 난이도: 골드4
기본 최소 신장 트리 문제
16398 행성 연결 문제풀이
백준 10423 전기가 부족해 / 난이도: 골드2
가상의 정점을 생각해야 하는 문제
10423 전기가 부족해 문제풀이
