다익스트라 알고리즘은 한 정점에서 다른 정점들 까지의 최단거리를 계산하는 알고리즘이다.
다익스트라 알고리즘 과정
- 시작점으로 둘 정점을 지정한다.
- 최단거리 테이블을 초기화한다.
- 시작점으로부터 거리가 최소인 정점을 선택,방문처리
- 선택된 정점과 인접한 정점의 거리를 구하고 최단거리 테이블을 초기화 한다.
- 3,4번을 반복한다.
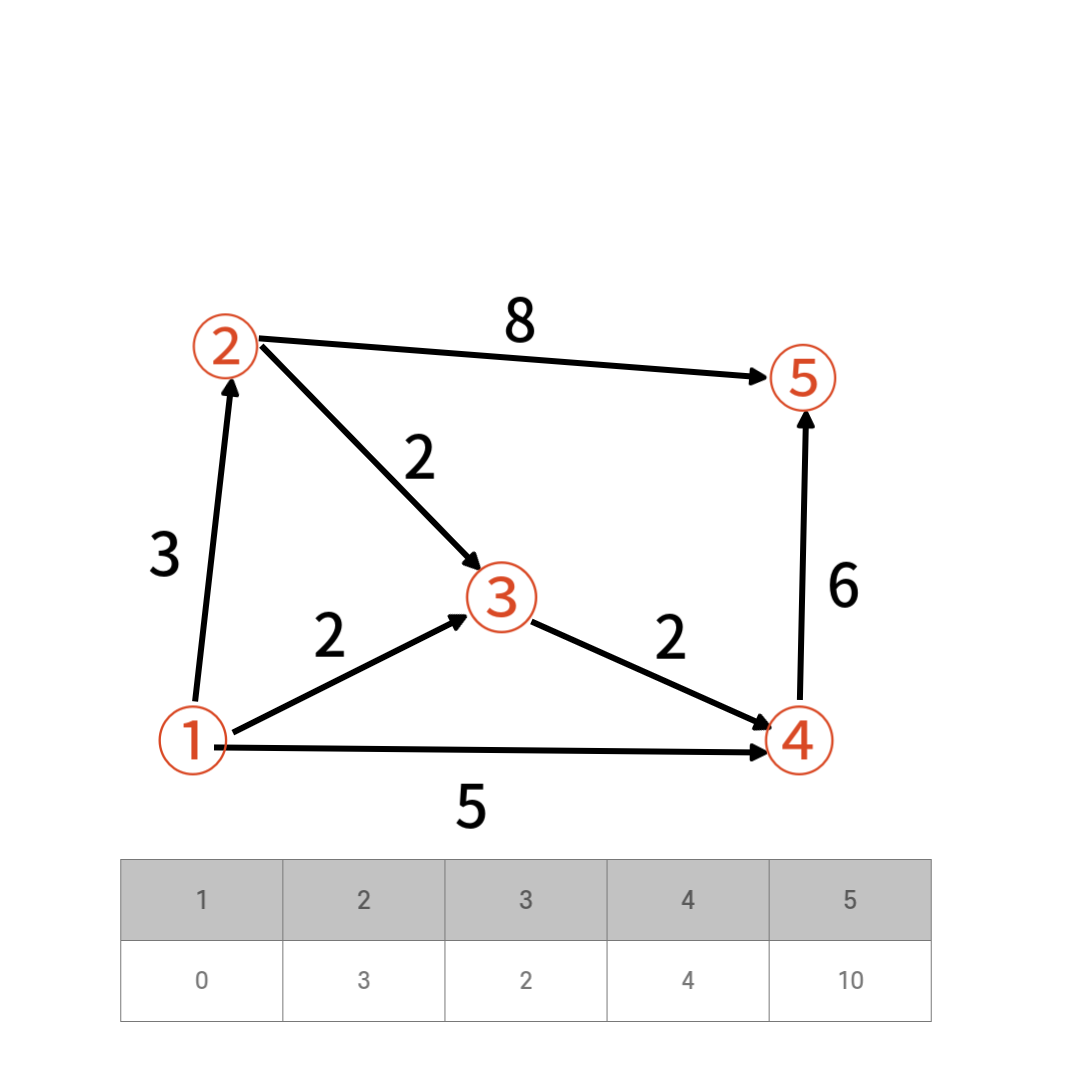
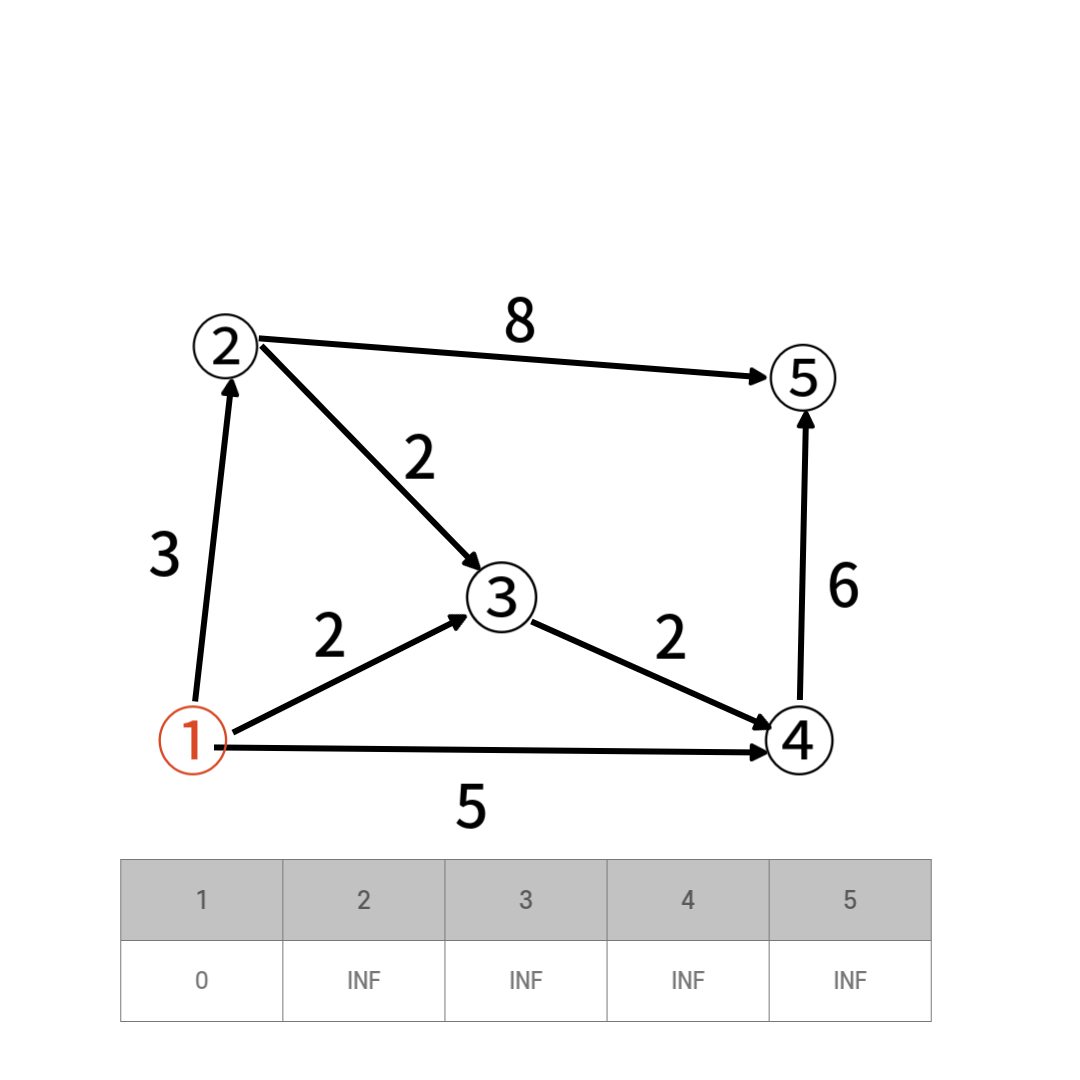1번 정점을 시작정점으로 지정하고 최단거리 테이블을 초기화한다
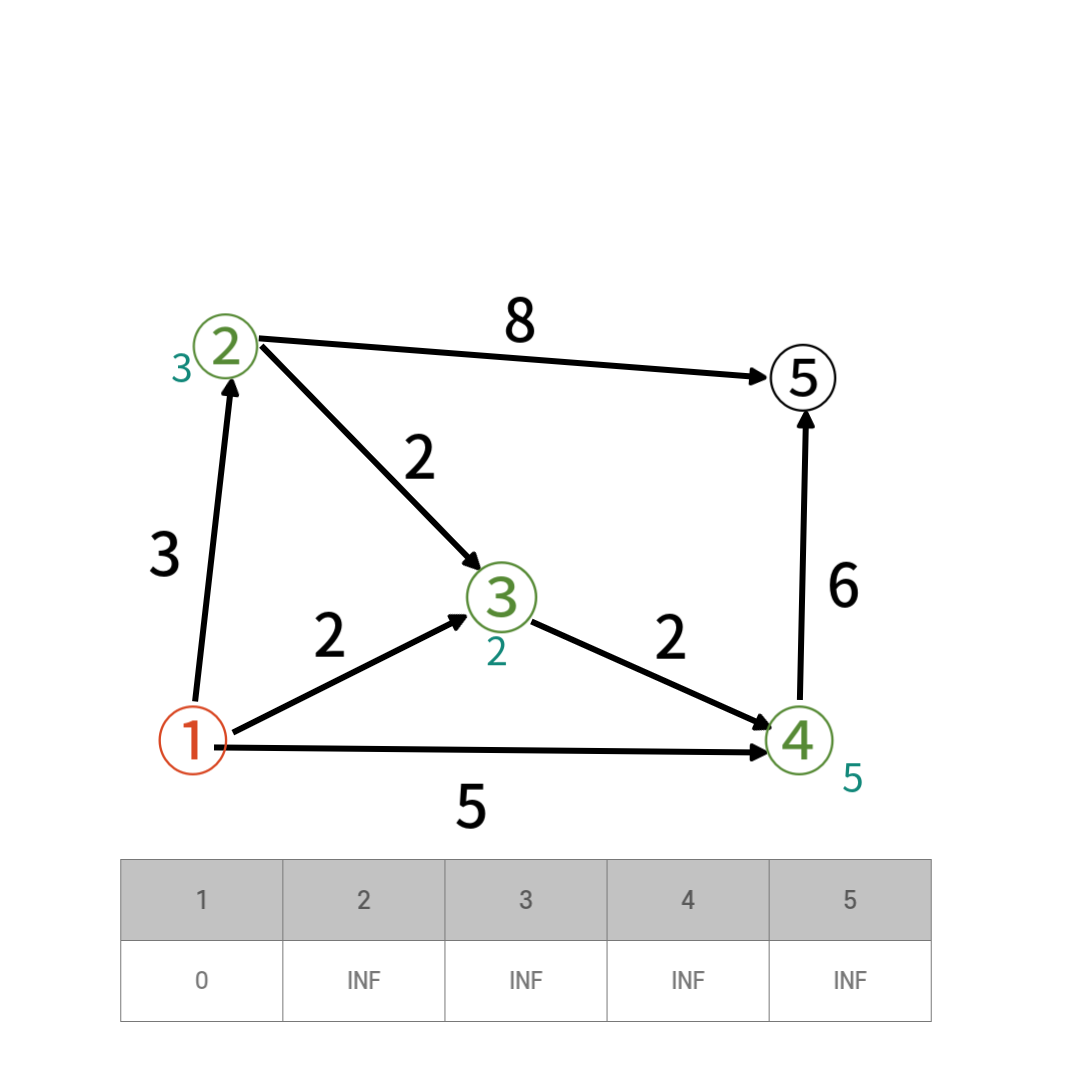1번 정점과 인접한 정점은 2,3,4번 정점이고 거리는 각 3,2,5다
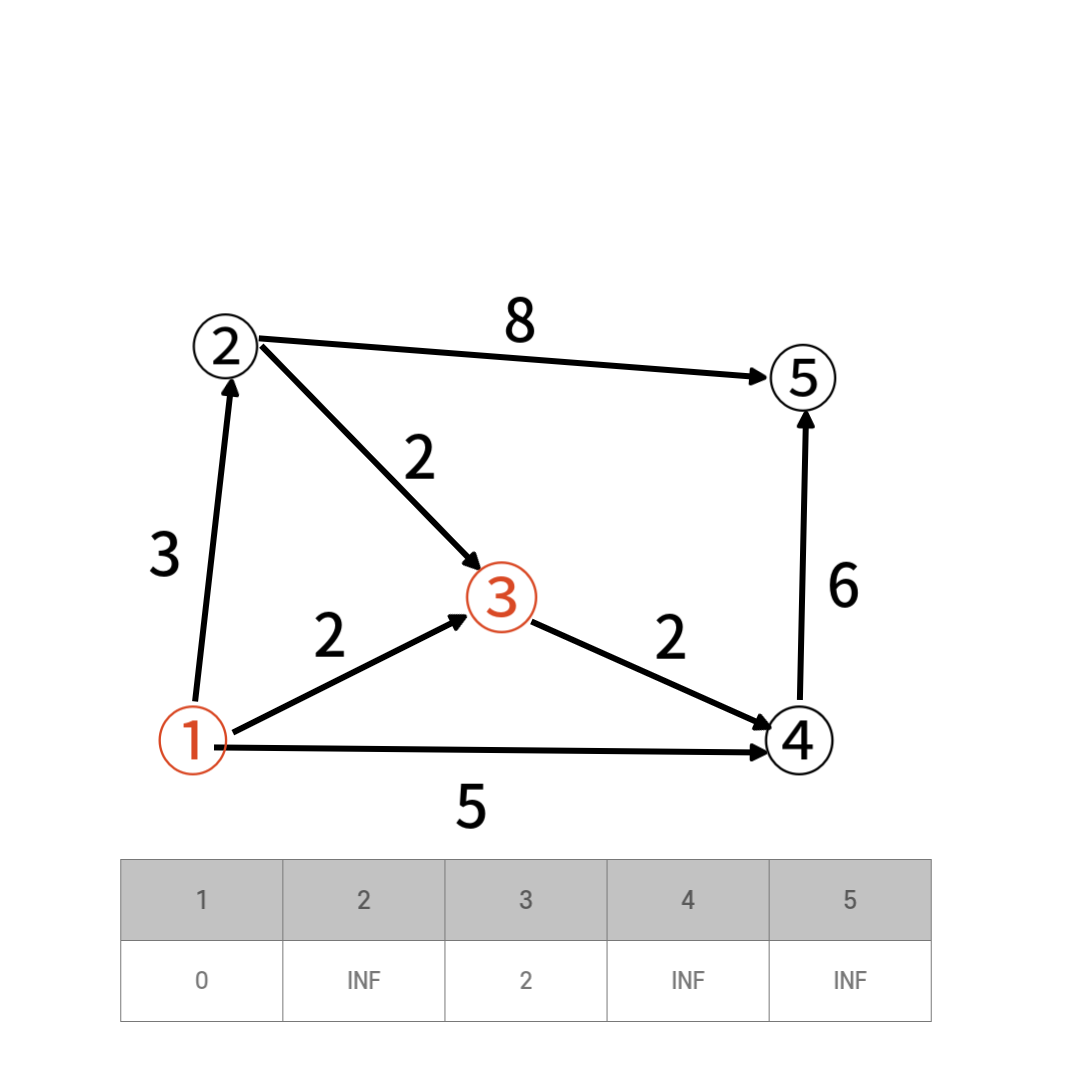거리가 가장 가까운 3번정점을 선택하고 방문처리 한다.
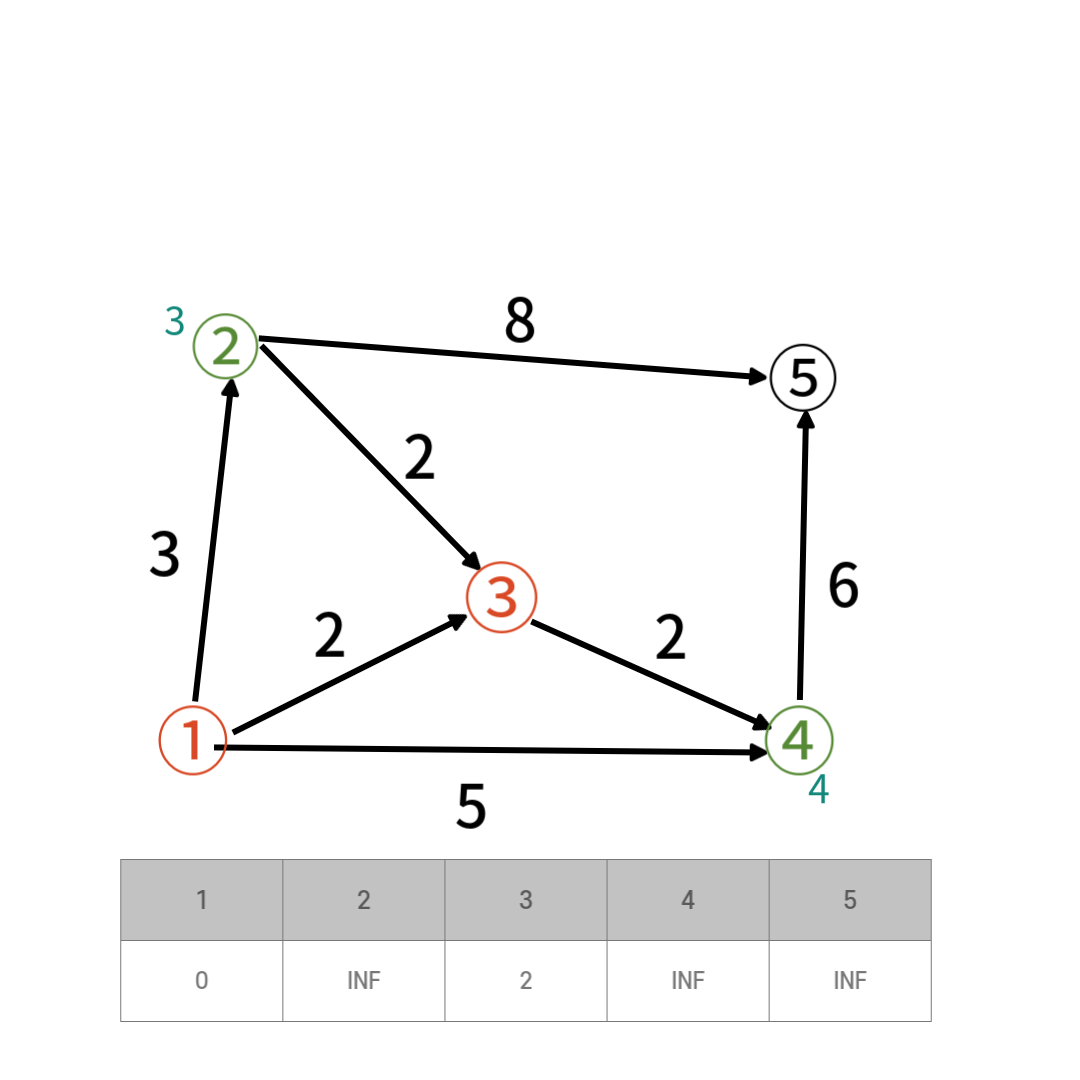선택된 1번 3번 정점에서 갈 수 있는 정점은 2,3번 정점이고 거리는 각 정점까지의 거리는 3,4이다.
여기서 4번정점 까지의 거리는 1 -> 3 -> 4 과정으로 갈때 최소이다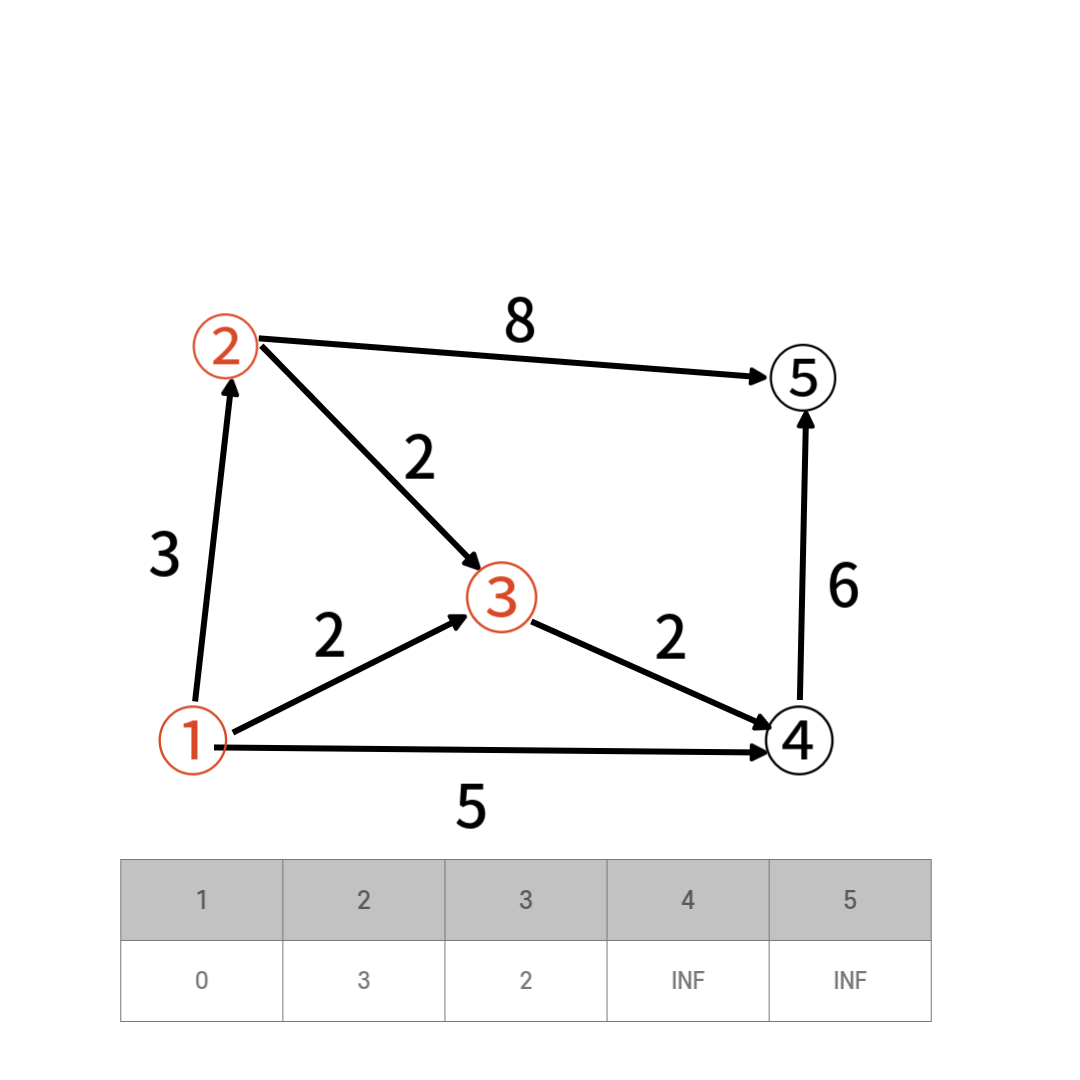
거리가 최소인 2번정점을 선택하고 방문 처리한다
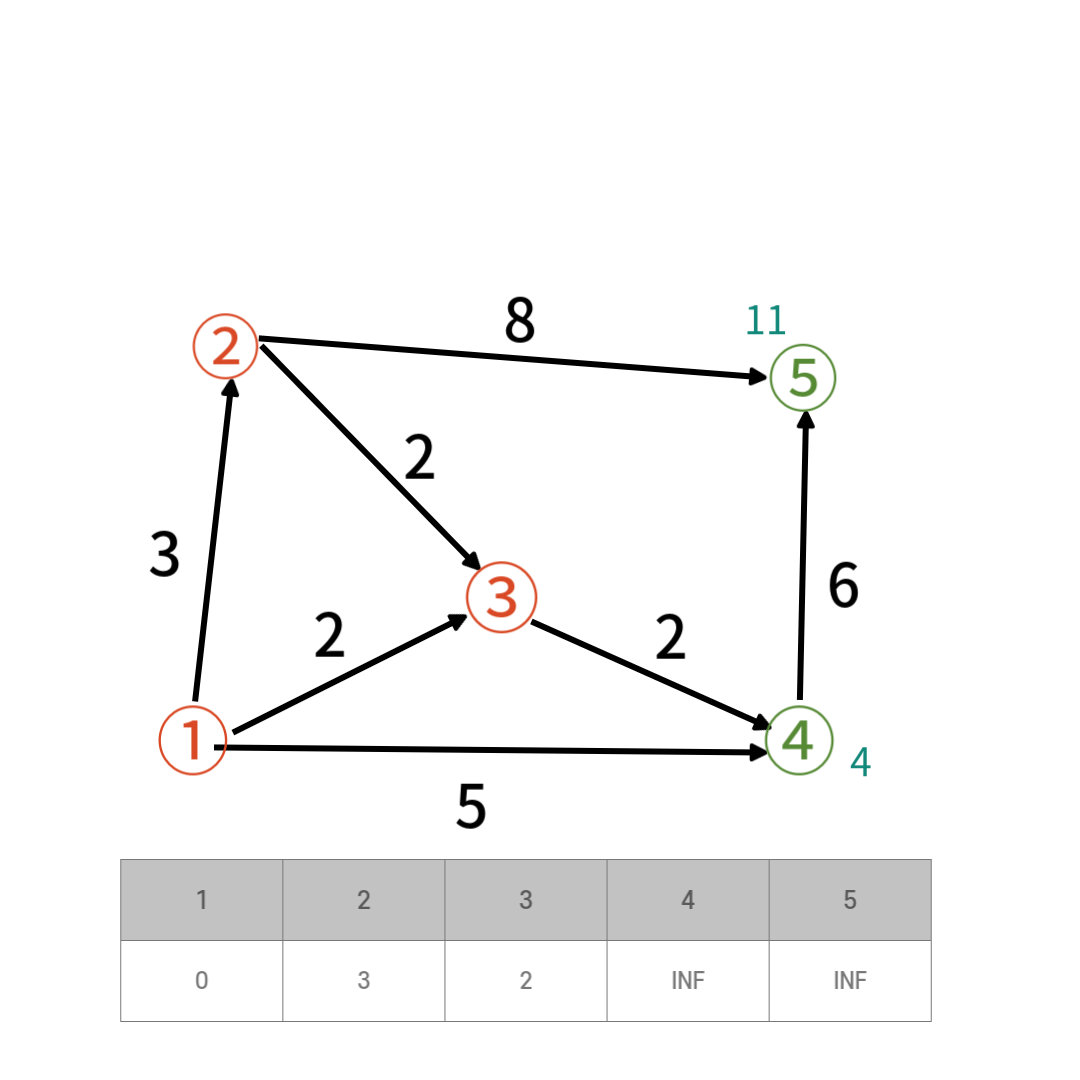선택된 1번 3번 2번정점에서 갈 수 있는 정점은 4,5번 정점이고 거리는 각 정점까지의 거리는 4,11이다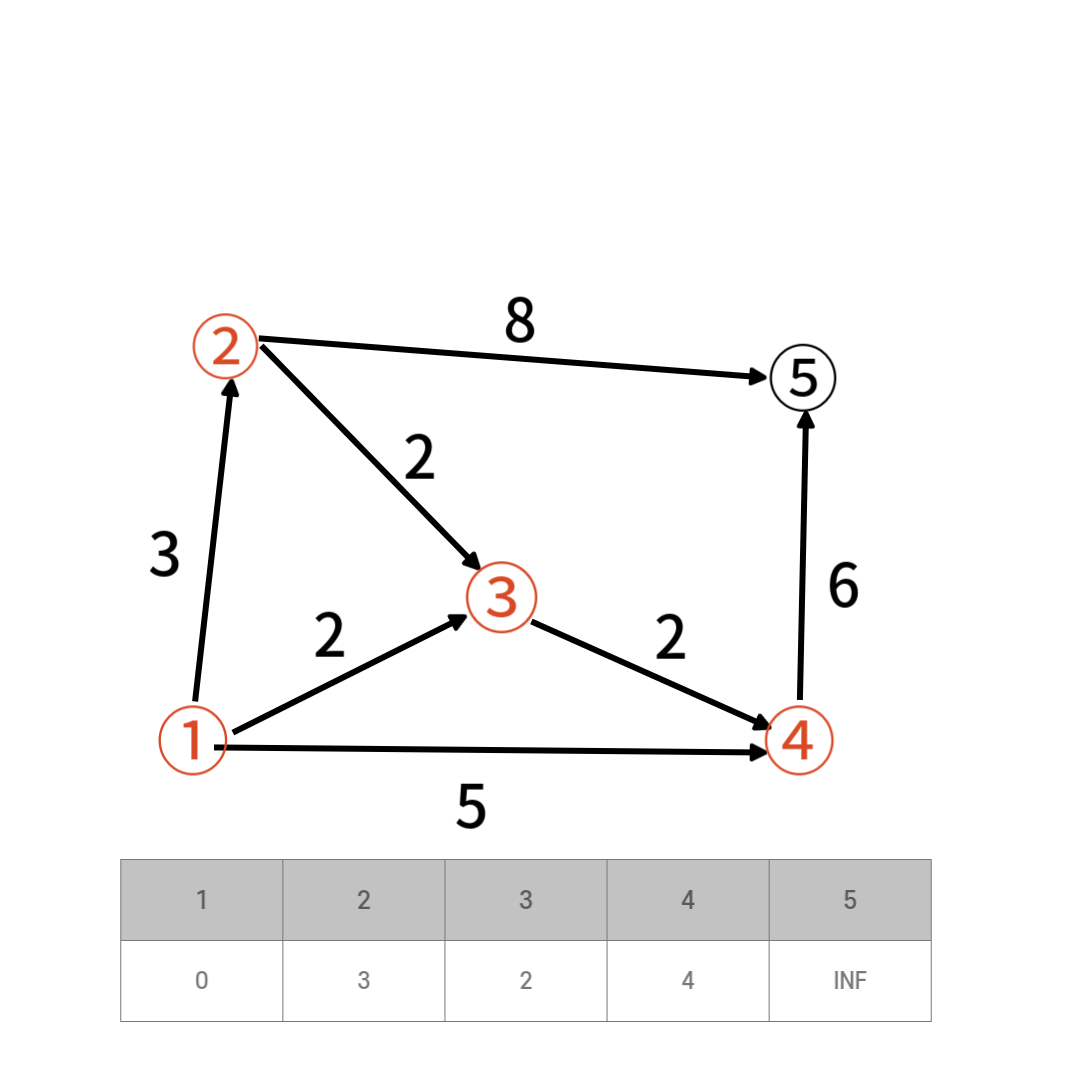
거리가 최소인 4번정점을 선택하고 방문 처리한다
위와 같은 과정을 반복하여 최단거리 테이블을 채운다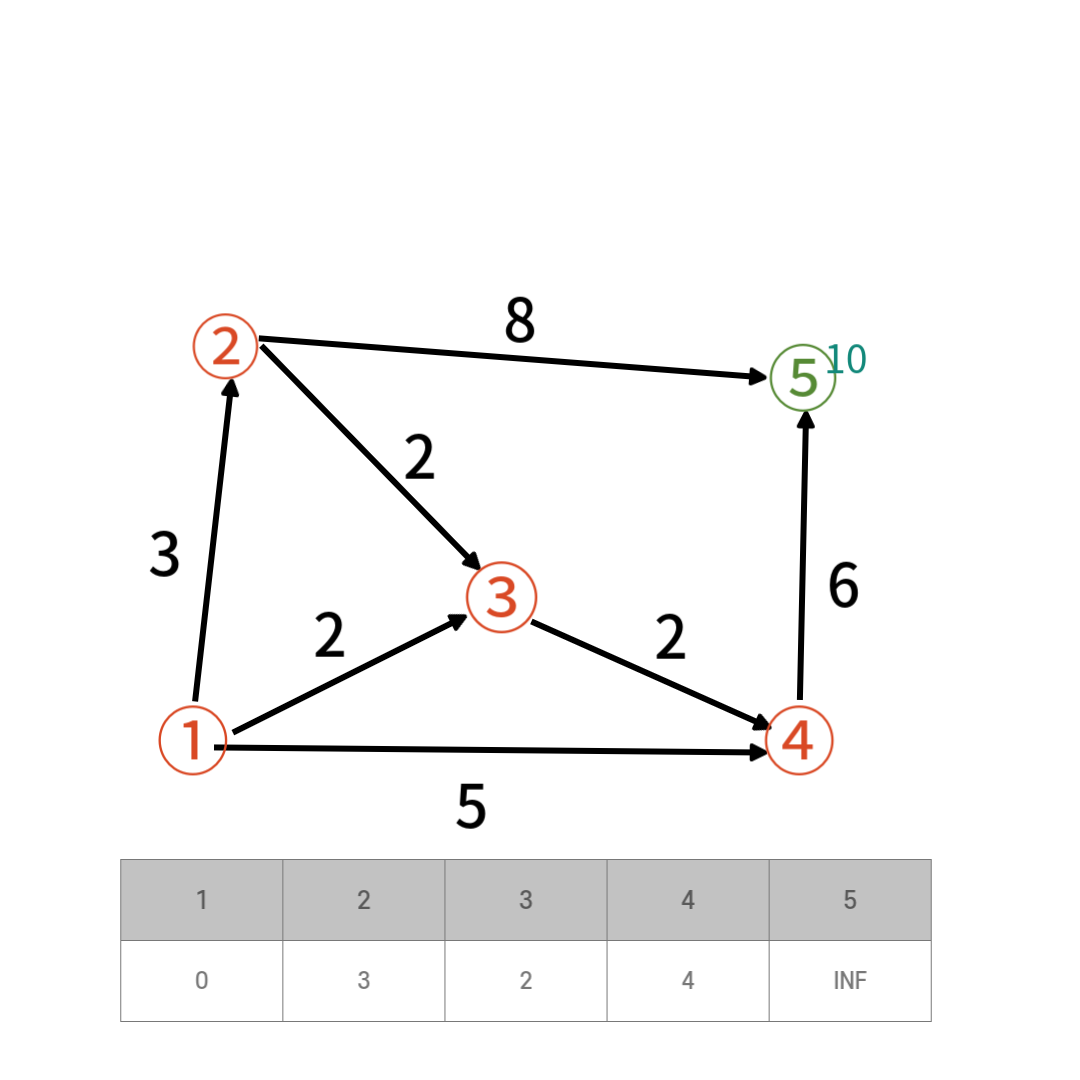
다익스트라 알고리즘 구현
#include <bits/stdc++.h>
using namespace std;
vector <pair<int,int>> adj[6]; //<비용 ,간선 번호>
int dist[6];
bool vis[6];
const int INF = 1e9;
int v = 6;
void Dijkstra(int st)
{
//모든 정점의 거리를 INF로 설정하고 시작 정점의 거리를 0으로 둔다
fill(dist,dist+6+1,INF);
dist[st] = 0;
int idx = st;
while(true)
{
int idx = -1;
//선택된 정점을 제외하고 가장 가까운 정점을 찾는다
for(int i=1; i<=6; i++)
{
if(vis[i])
continue;
if(idx == -1)
idx = i;
else if(dist[i] < dist[idx])
idx = i;
}
//선택할 정점이 없으면 반복문을 나간다
if(idx == -1)
break;
vis[idx] = true; // 가장 가까운 정점을 방문처리한다
for(auto nxt : adj[idx])
{
dist[nxt.second] = min(dist[nxt.second], dist[idx]+nxt.first);
}
}
}위 과정을 토대로 구현한 다익스트라 알고리즘이다.
dist배열은 최단거리 테이블을 나타낸 것이고 vis배열은 선택된 정점을 방문처리 한 것이다
이와 같은 방법의 구현은 시간복잡도가 O(V2+E) 이다.
우선순위 큐를 이용한 다익스트라 알고리즘
다익스트라 알고리즘을 구현하는 다른 한가지 방법은
우선순위 큐를 사용하는 방법인데 이 방법은 시간 복잡도가 O(ElgE) 이다.
첫번째 방법은 알고리즘 실행 시 거리가 최소인 하나의 정점만 최단거리를 업데이트했지만, 우선순위 큐를 사용했을땐 선택된 정점과 인접한 정점의 거리를 모두 업데이트 한다는 차이점이 있다.
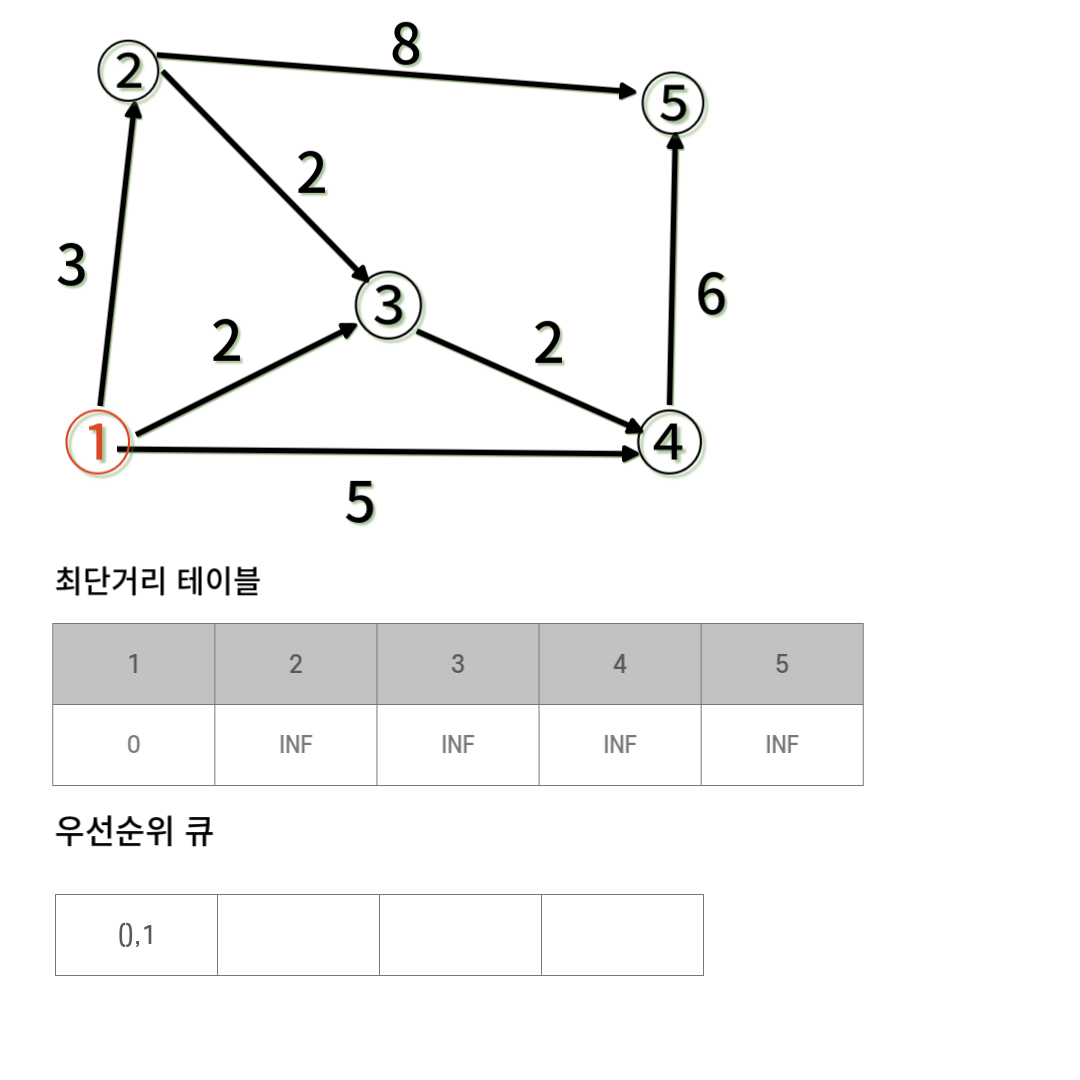
<거리,정점>으로 되어있는 우선순위 큐에시작점의 거리와 정점을 넣는다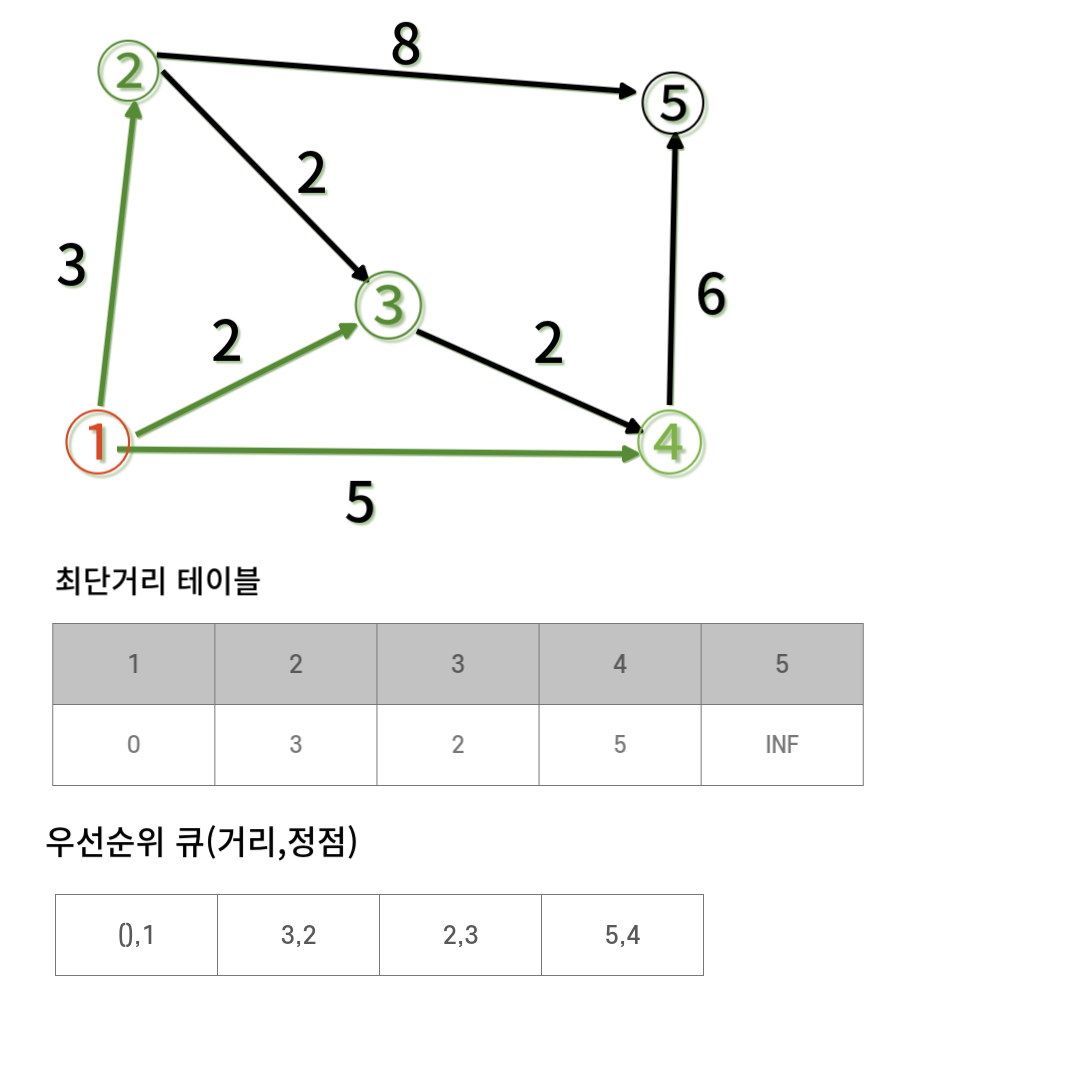
우선순위 큐의 가장 첫번째에 있는 정점과 인접한 정점들의 거리를 최단거리 테이블에 추가하고 우선순위 큐에 추가한다.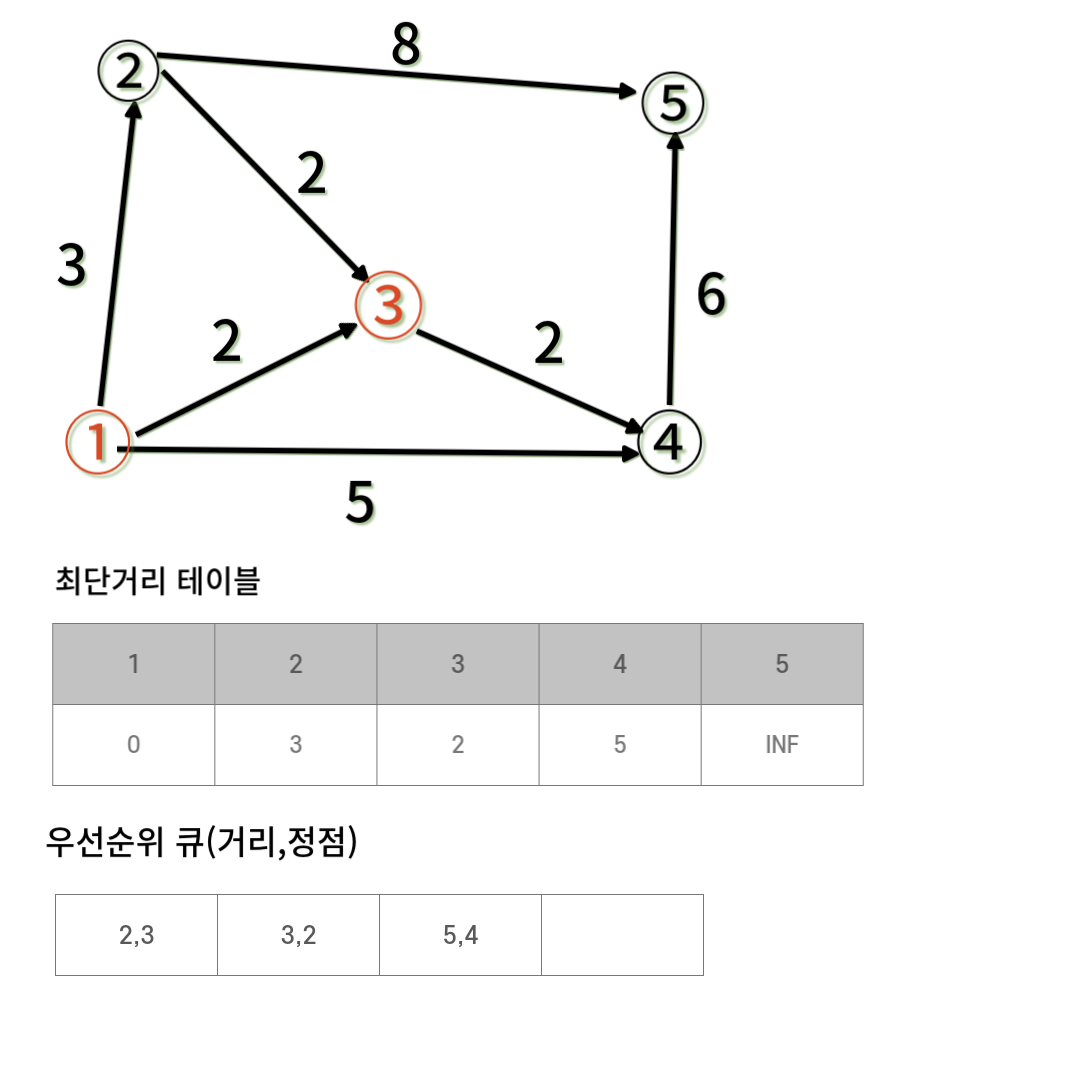
그 다음에 우선순위 큐에 첫번째는 2,3이 된다. 3번 정점과 인접한 정점의 최단거리를 구하고 우선순위 큐에 추가한다.
이와 같은 과정을 반복한다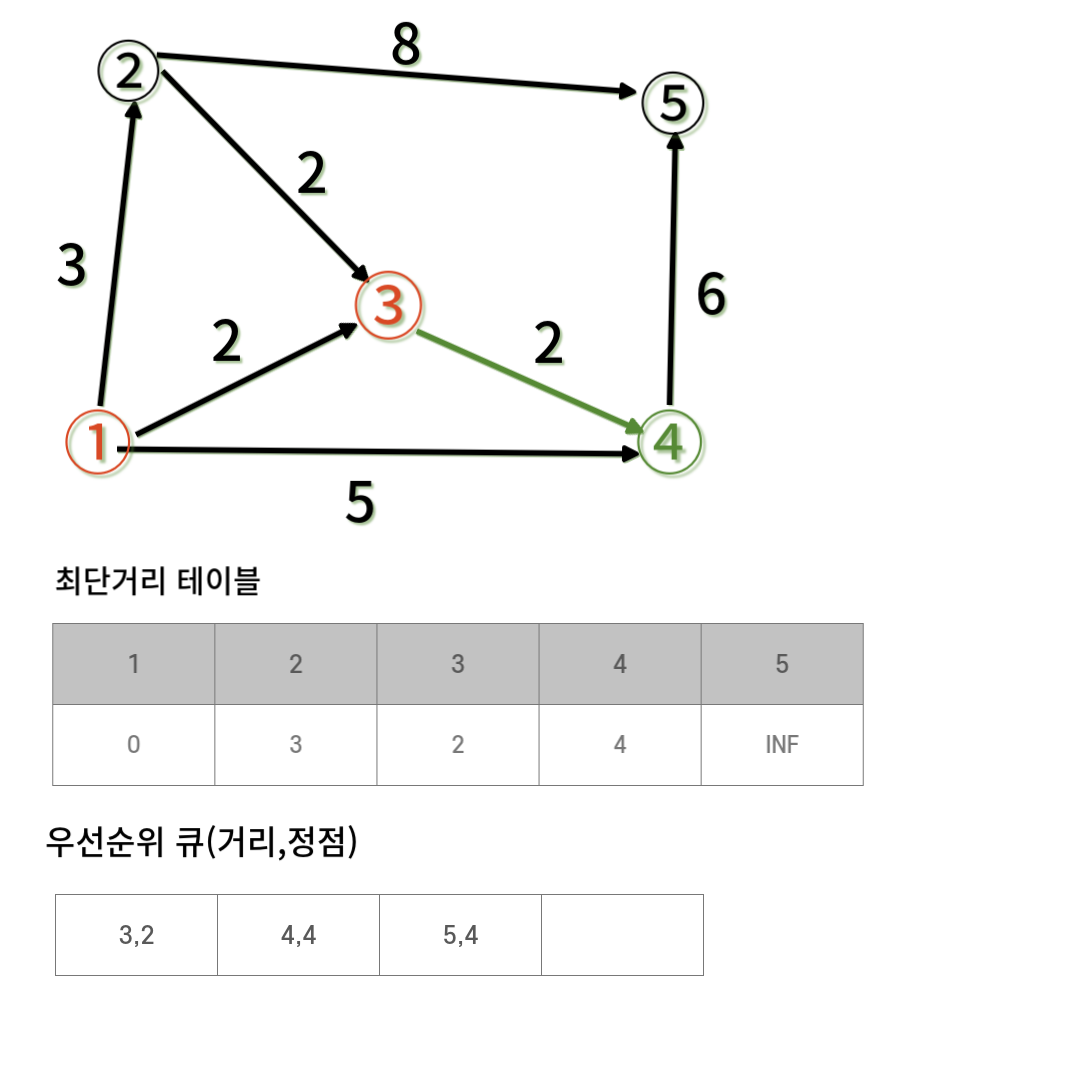
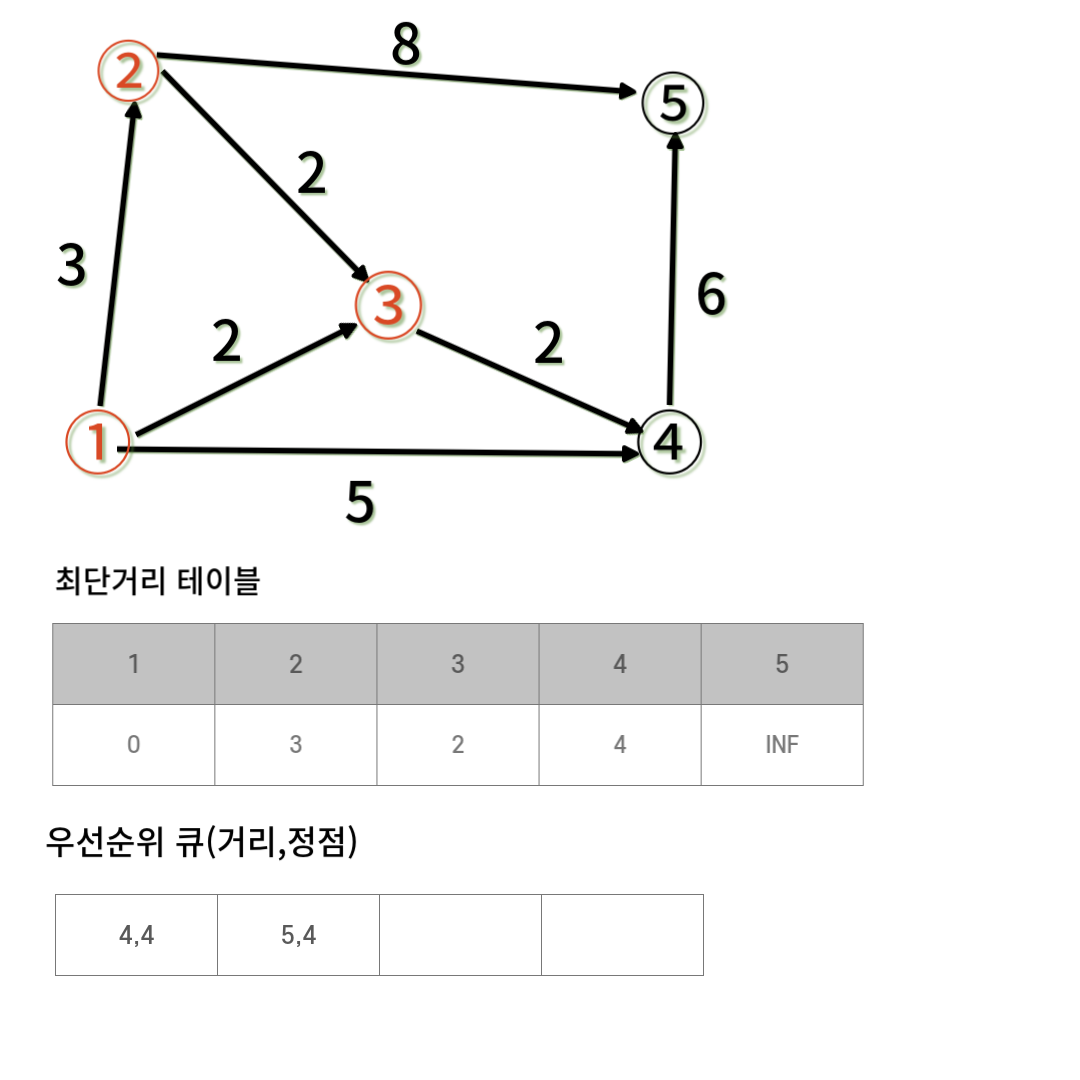다음 과정은 생략하고 바로 구현 코드를 보자
#include <bits/stdc++.h>
using namespace std;
vector <pair<int,int>> adj[7];
priority_queue <pair<int,int>, vector<pair<int,int>>,
greater <pair<int,int>> > pq;
int dis[7];
int INF = 1e9;
int n = 6;
void dijkstra(int start)
{
fill(dis,dis+n+1, INF);
dis[start] = 0;
pq.push({0,start});
while(!pq.empty())
{
auto idx = pq.top();
pq.pop();
//최솟값으로 갱신이 여러번 됐을때 이전에 갱신된 값이 들어갈 수 있기 때문
if(dis[idx.second] != idx.first)
continue;
for(auto nxt : adj[idx.second])
{
if(dis[nxt.first] > dis[idx.second] + nxt.second)
{
dis[nxt.first] = dis[idx.second] + nxt.second;
pq.push({dis[nxt.first],nxt.first});
}
}
}
}
if(dis[idx.second] != idx.first)
continue;
이 코드가 이해가 안 될 수 있는데
위에 과정에서 우리는 4번정점까지의 거리를 우선순위 큐에 넣을때 (5,4)를 넣었던 적이 있다.
하지만 (4,4)를 넣게 됨으로써 최단거리는 4가 되고 (5,4)는 버려야하는 상황이 되었다. 따라서 최단거리 테이블에 있는 거리와 우선순위 큐에 들어있는 거리가 다르면 건너뛴다.
다익스트라 알고리즘 관련 문제
1753번 최단경로 / 난이도: 골드4
위에서 배운 기본적인 다익스트라 알고리즘을 활용하는 문제
1753 최단경로 문제풀이
1504번 특정한 최단경로 / 난이도: 골드4
다익스트라를 여러 번 사용해야하는걸 생각해야하는 문제
1504 특정한 최단경로 문제풀이
17835번 면접보는 승범이네 / 난이도: 골드2
그래프를 역방향으로 생각해야 하는 문제
17835 면접보는 승범이네 문제풀이
