[알고리즘] 위상 정렬(Topological Sort)

Flame🔥·2023년 10월 27일

알고리즘

목록 보기

3/5

1.위상 정렬이란?

위상 정렬은 방향 그래프에서 정점간의 선수 관계를 위배하지 않도록 나열하는 정렬이다.

2.위상 정렬 과정

간선을 입력받으며 indegree 테이블을 채운다.
2.indegree가 0인 정점들을 큐에 넣는다
3.큐에서 정점을 꺼내 위상 정렬 결과에 추가한다.
4.결과에 추가된 정점과 연결된 모든 정점의 indegree값을 1 감소시킨다. 이때 indegree값이 0이 된다면 정점을 큐에 추가한다.
5.큐가 빌 때 까지 3,4번 과정을 반복한다

여기서 indegree는 자신의 정점으로 들어오는 간선의 수를 말한다.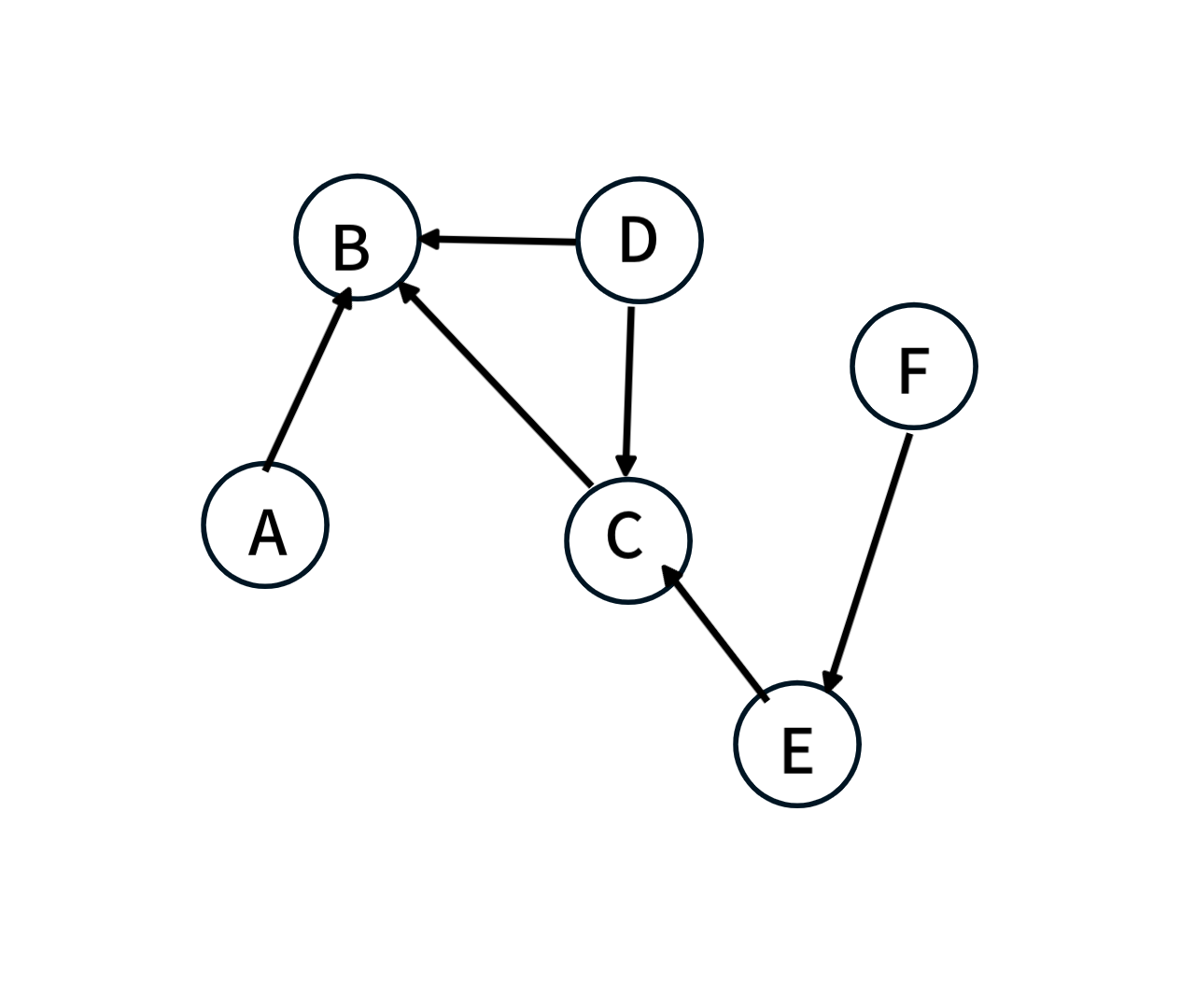
위와 같은 그래프에서 indegree는 A:0 B:3 C:2 D:0 E:1 F:0 이다.

그러면 과정을 그림을 통해 살펴보자
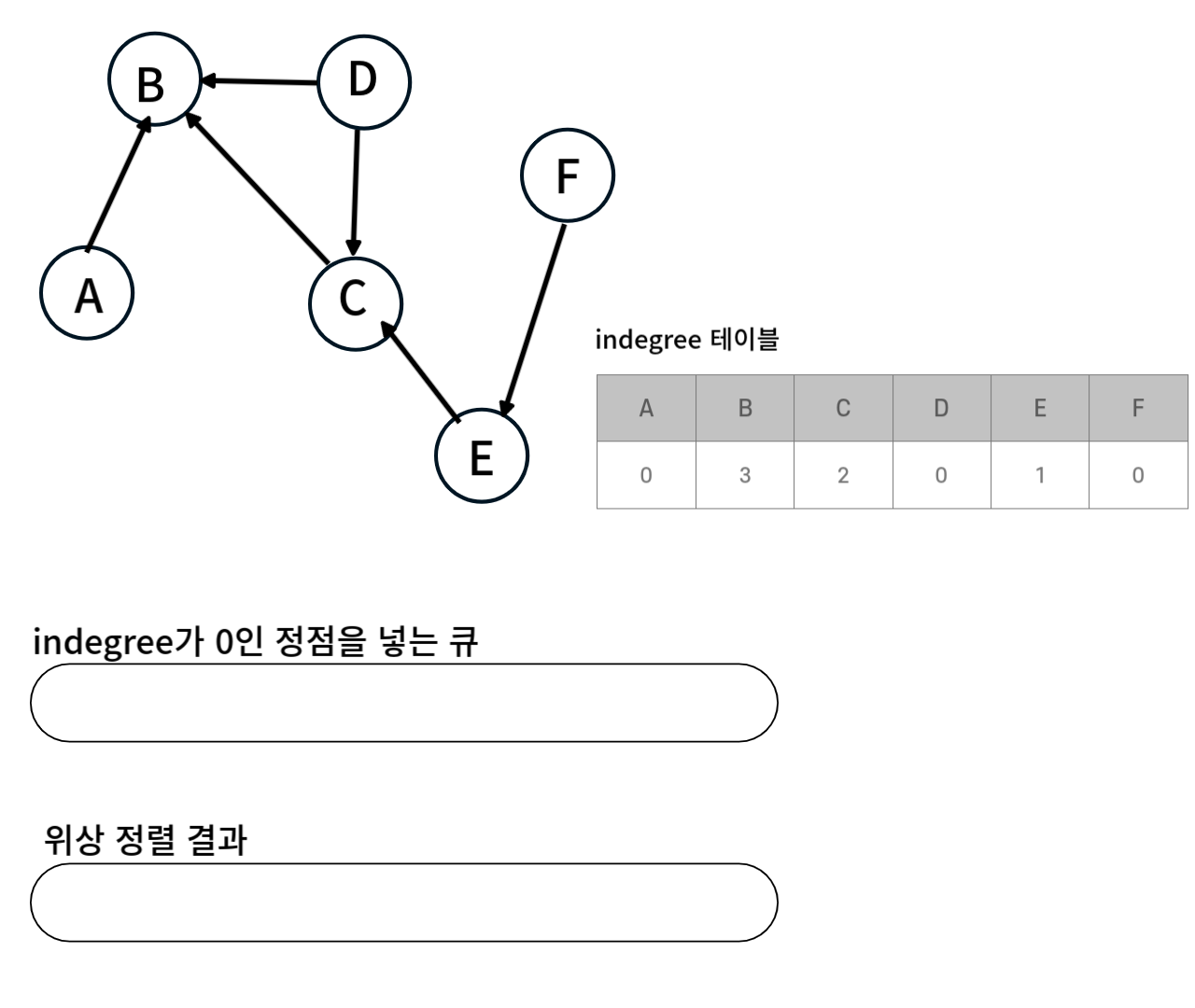각 정점의 indegree를 입력받고 배열에 넣는다
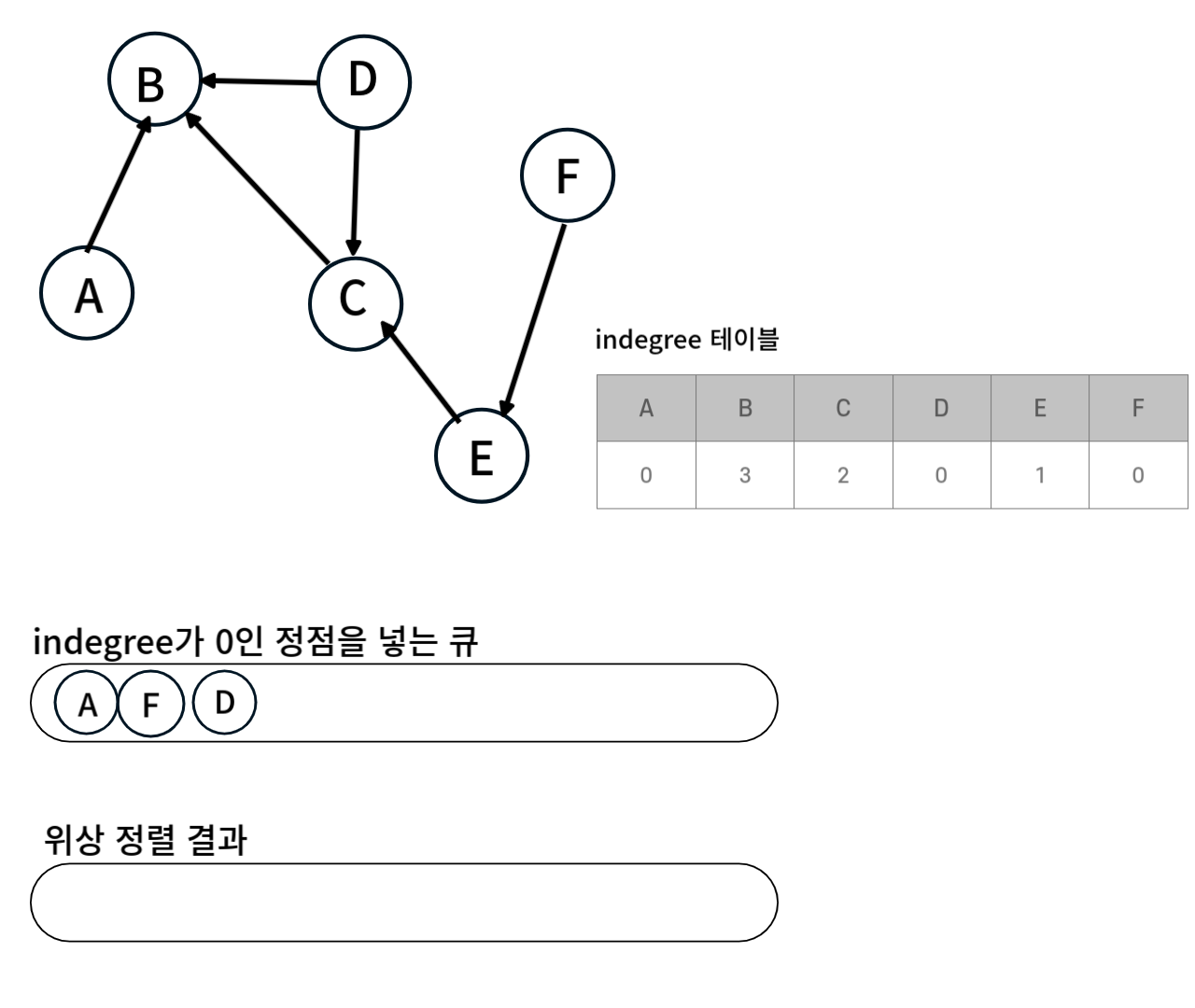indegree가 0인 정점을 큐에 모두 넣는다
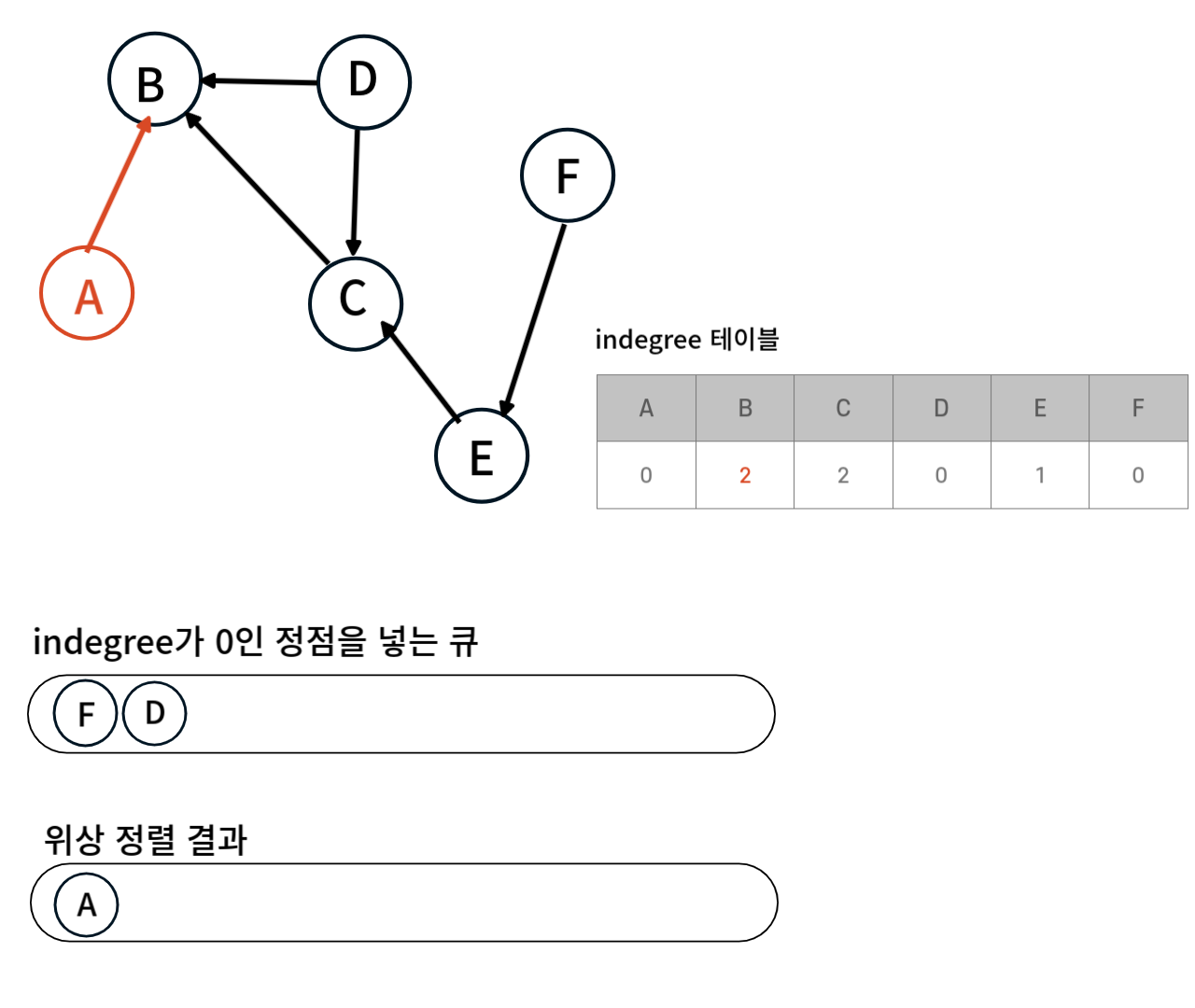큐의 맨 앞에 있는 A를 위상 정렬 결과에 추가한 뒤 A가 가르키고 있는 정점인 B의 indegree값을 1 감소시킨다.
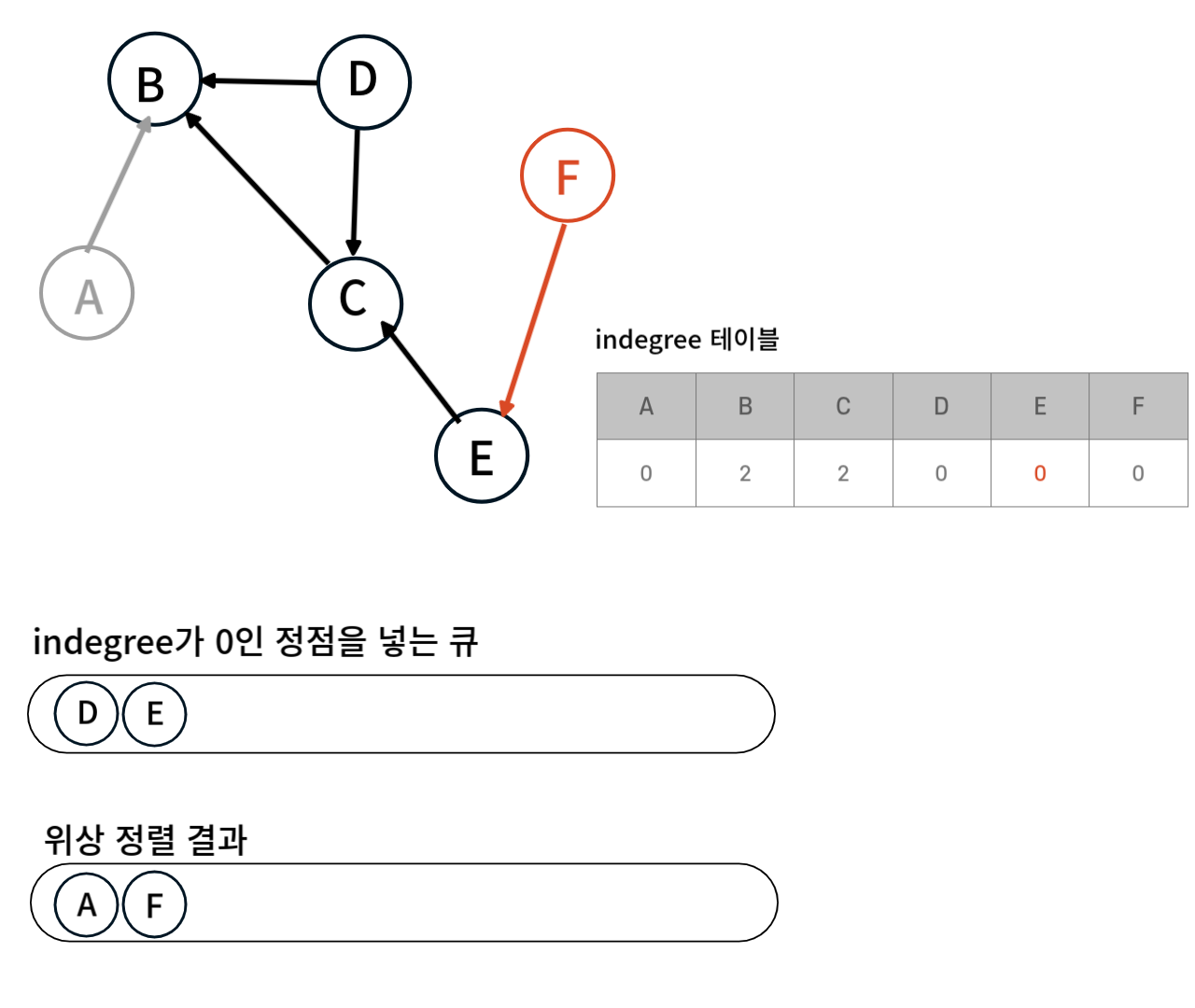큐의 맨 앞에 있는 F를 위상 정렬 결과에 추가한 뒤 F가 가르키고 있는 정점인 E의 indegree값을 1 감소시킨다. 이 때 E의 indegree값이 0이 되었으므로 큐에 추가한다.
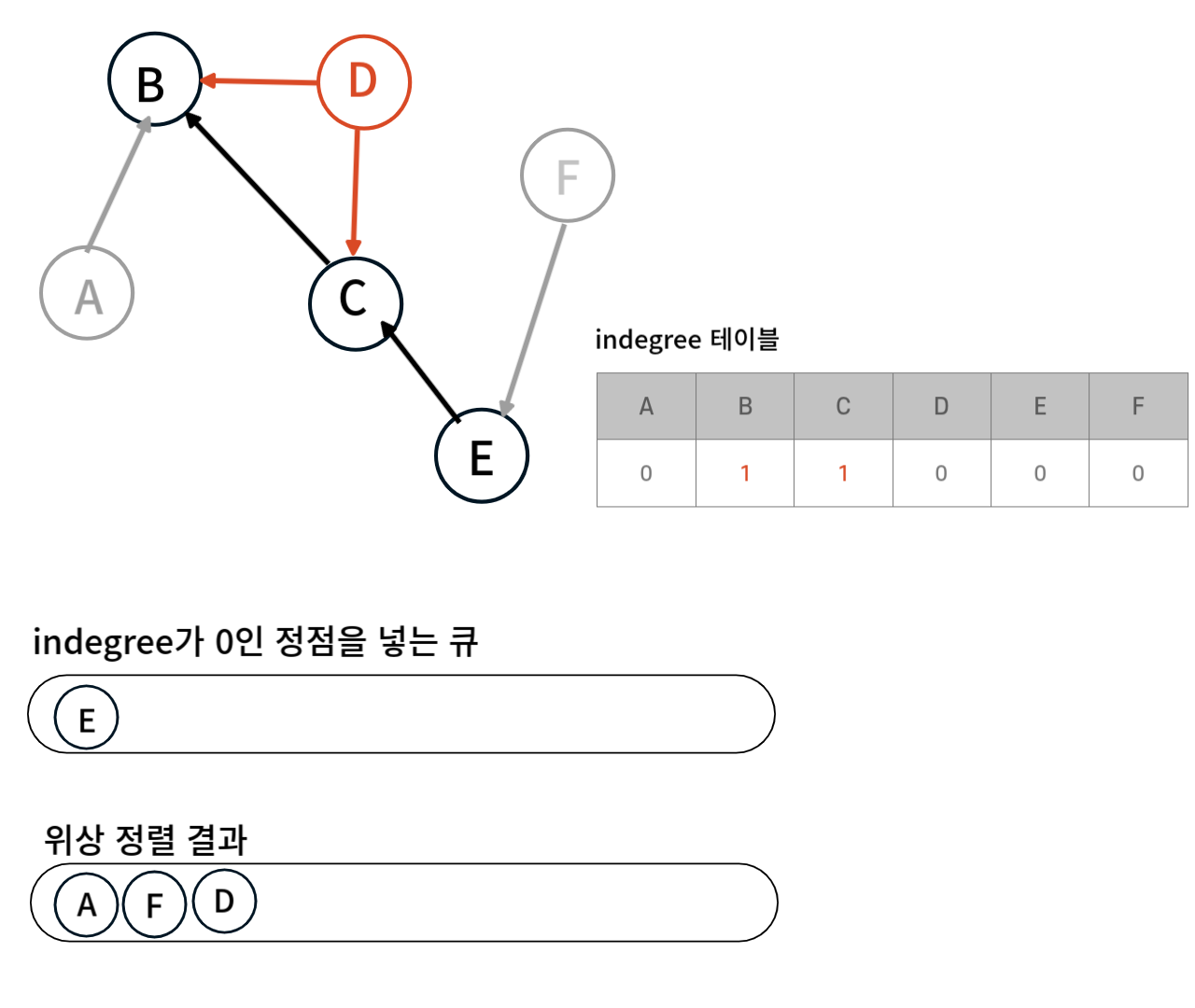큐의 맨 앞에 있는 D를 위상 정렬 결과에 추가한 뒤 D가 가르키고 있는 정점인 B와 C의 indegree값을 1 감소시킨다.
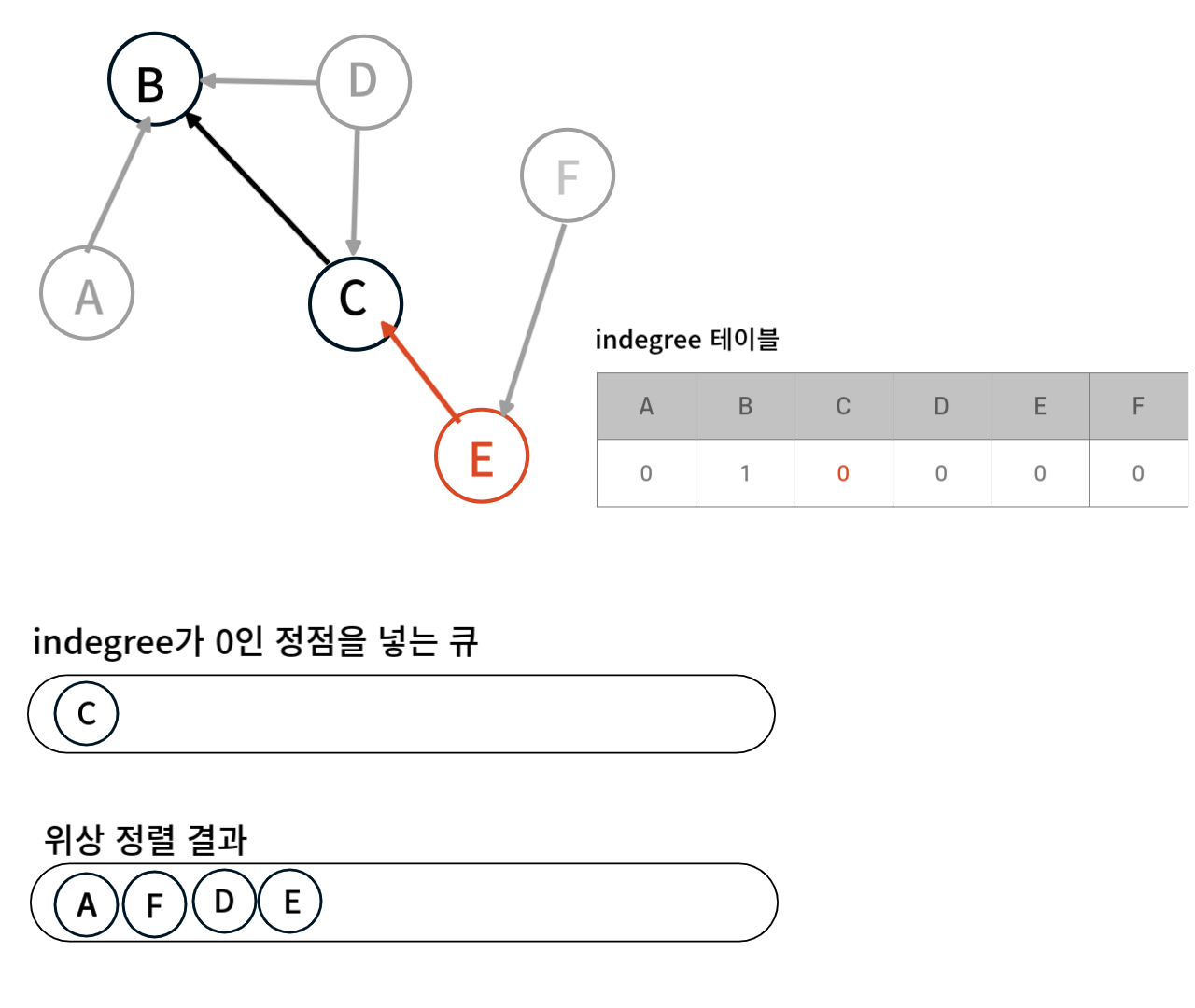큐의 맨 앞에 있는 E를 위상 정렬 결과에 추가한 뒤 E가 가르키고 있는 정점인 C의 indegree값을 1 감소시킨다. 이 때 C의 indegree값이 0이 되었으므로 큐에 추가한다.
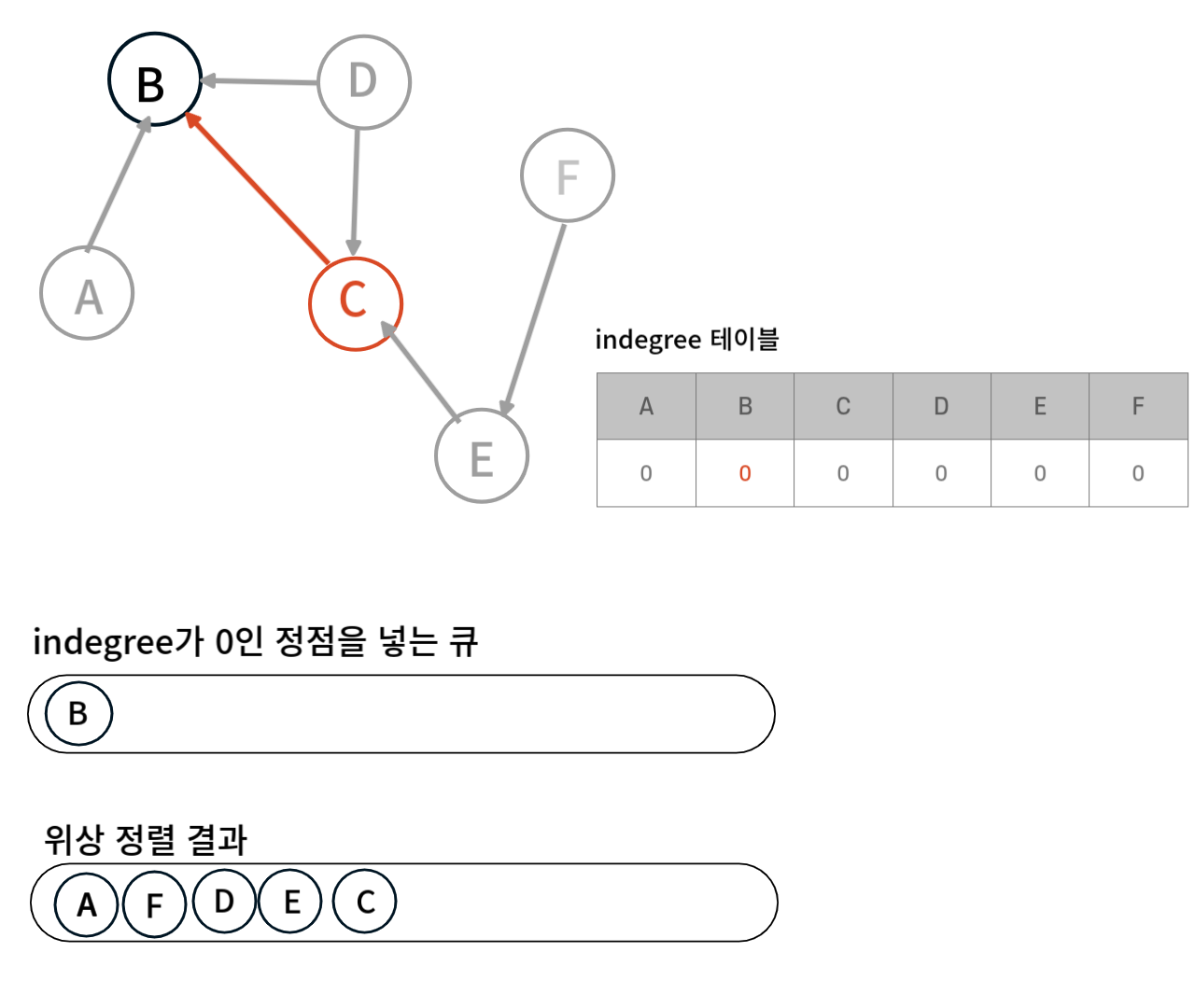앞의 과정 반복
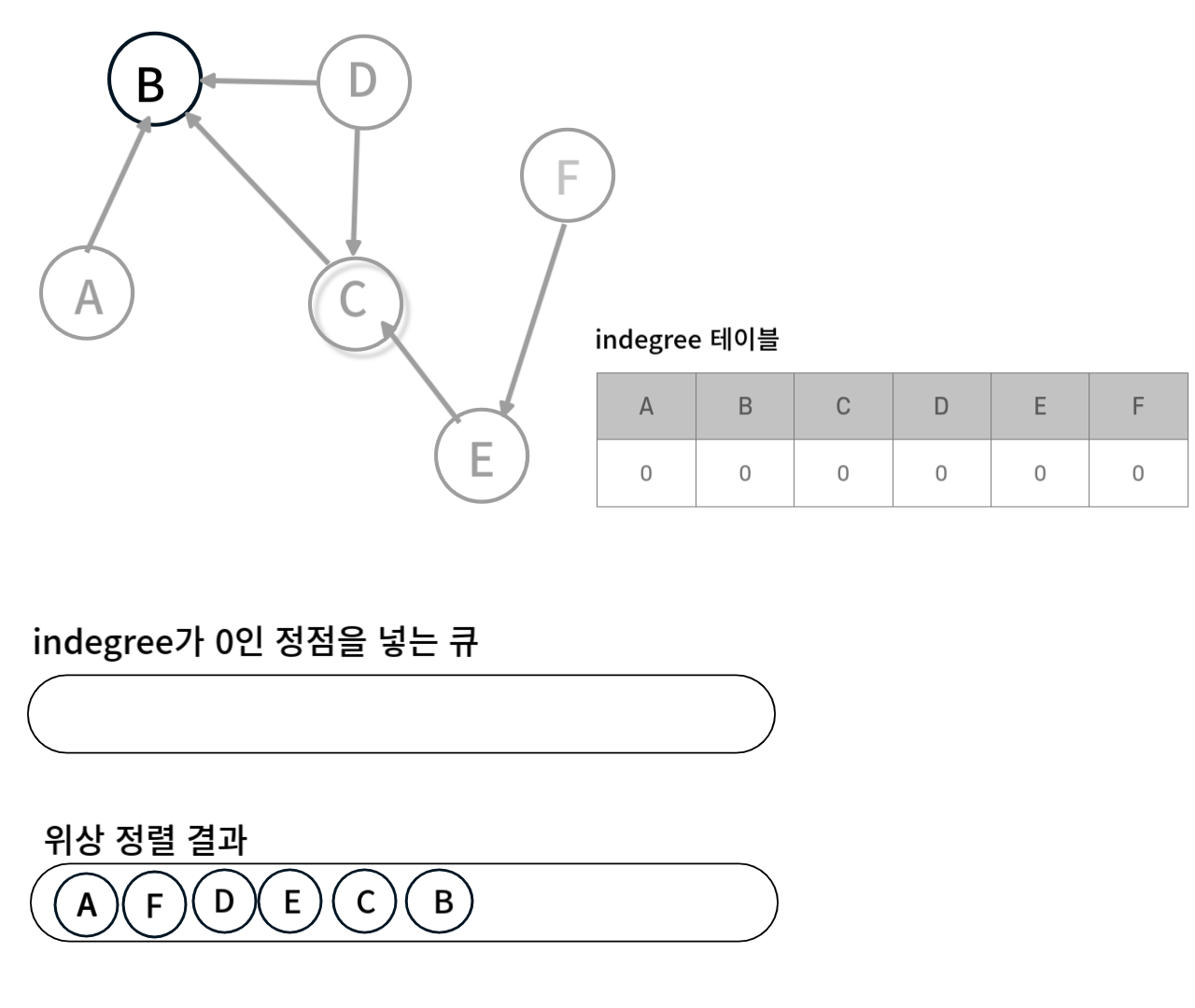큐가 비게 되면 위상 정렬의 과정이 끝나게 된다.

그래프에 사이클이 있을 때는 indegree가 0이 될 수 없어 위상 정렬이 불가능하다

3. 위상 정렬 코드

#include <bits/stdc++.h>
using namespace std;

vector <int> adj[32001];
vector <int> res;
int indegree[32001];

void topological_sort(int n)
{
    queue <int> q;
    //가장 먼저 indegree가 0인 정점을 큐에 추가한다
    for(int i=1; i<=n; i++)
    {
        if(indegree[i] == 0)
            q.push(i);
    }

    while(!q.empty())
    {
        //큐에서 정점을 꺼내 위상 정렬 결과에 추가한다.
        int cur = q.front();
        res.push_back(cur);
        q.pop();
        
        
        for(int nxt:adj[cur])
        {
            //결과에 추가된 정점과 연결된 모든 정점의 indegree값 을 1 감소시킨다.
            indegree[nxt]--;
            
            //이때 indegree값이 0이 된다면 정점을 큐에 추가한다.
            if(!indegree[nxt])
                q.push(nxt);
        }
    }

    for(int ele : res)
        cout << ele << " ";
}    

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n,m;
    cin >> n >> m;
    
    int x,y;
    
    //x->y인 x와 y를 입력받고 y의 indegree값을 1증가시킨다
    for(int i=0; i<m; i++)
    {
        cin >> x >> y;
        adj[x].push_back(y);
        indegree[y]++;
    }

    topological_sort(n);
}