[알고리즘] 이분 탐색(Binary Search)

Flame🔥·2023년 11월 2일

cpp 알고리즘 이분탐색

알고리즘

목록 보기

4/5

1.이분 탐색이란?

이분 탐색은 정렬된 배열에서 배열을 반으로 쪼개가며 원하고자 하는 값을 찾는 알고리즘이다.

순차 탐색도 있는데 이분 탐색을 사용하는 이유는?
순차탐색은 시간복잡도가 O(n)이고 이분탐색은 시간복잡도가 O(log n) 더 빠르기 때문이다.

n의 값이 작으면 순차탐색이 빠르겠지만 n의 값이 커지면 이분탐색이 더 빨라진다.

2.이분 탐색 과정

배열을 오름차순으로 정렬한다

배열의 처음을 st, 마지막을 en으로 설정하고 mid를 (st+en)/2로 설정한다.

찾고자하는 값이 mid보다 크면 st = mid+1, 작으면 en = mid -1로 변경한다.

mid의 값을 바꿔준다 mid = (st+en)/2

찾고자하는 값이 mid가 될때까지 3,4번을 반복한다.

그림을 통해 살펴보자!!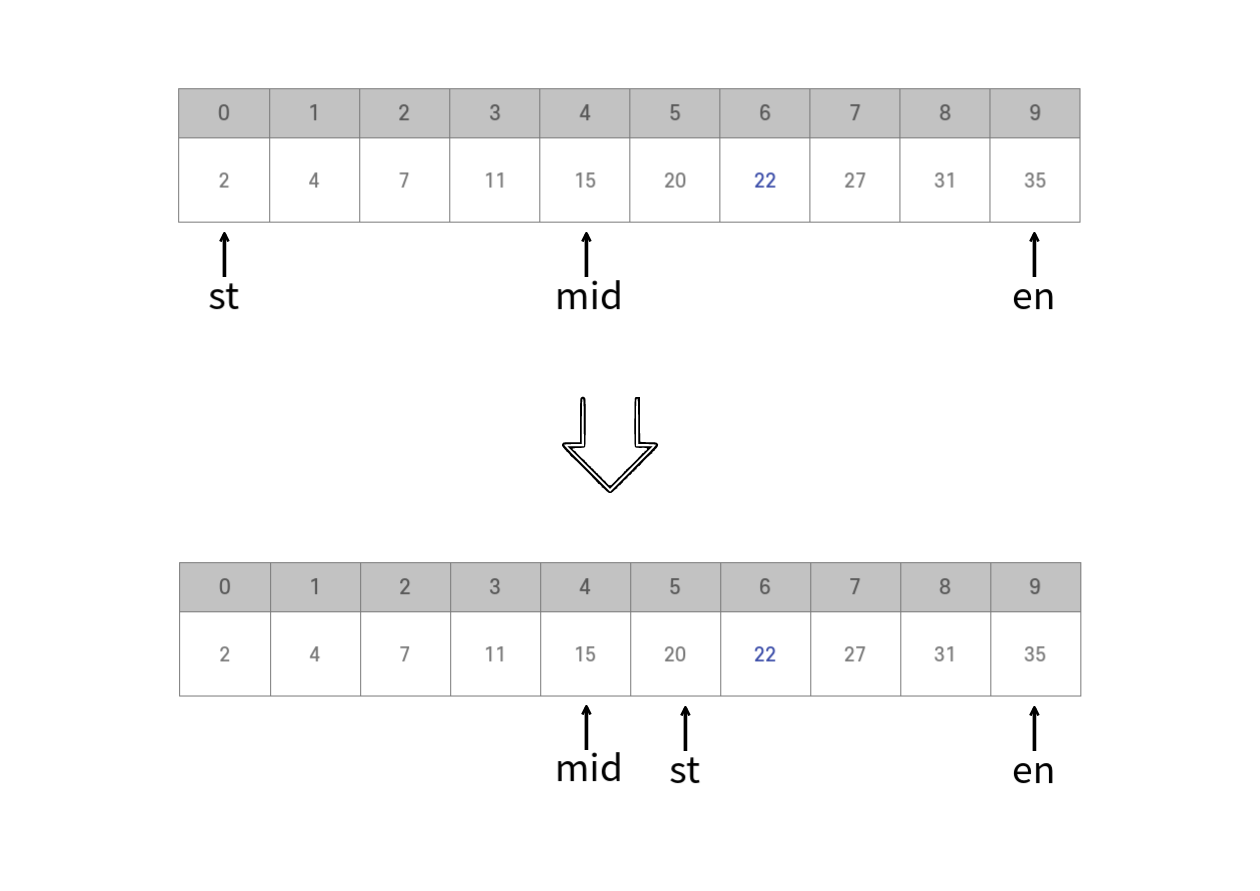우리가 찾고자하는 값을 22라고 하자.

오름차순으로 정렬된 배열에서 시작한다. 배열의 인덱스가 0부터 9까지이다. st=0, en=9, mid = (0+9) / 2 = 4

위 배열을 A라고 했을 때 A[mid] = 15 < 22 이다. 따라서 st = mid + 1 = 5로 변경한다.
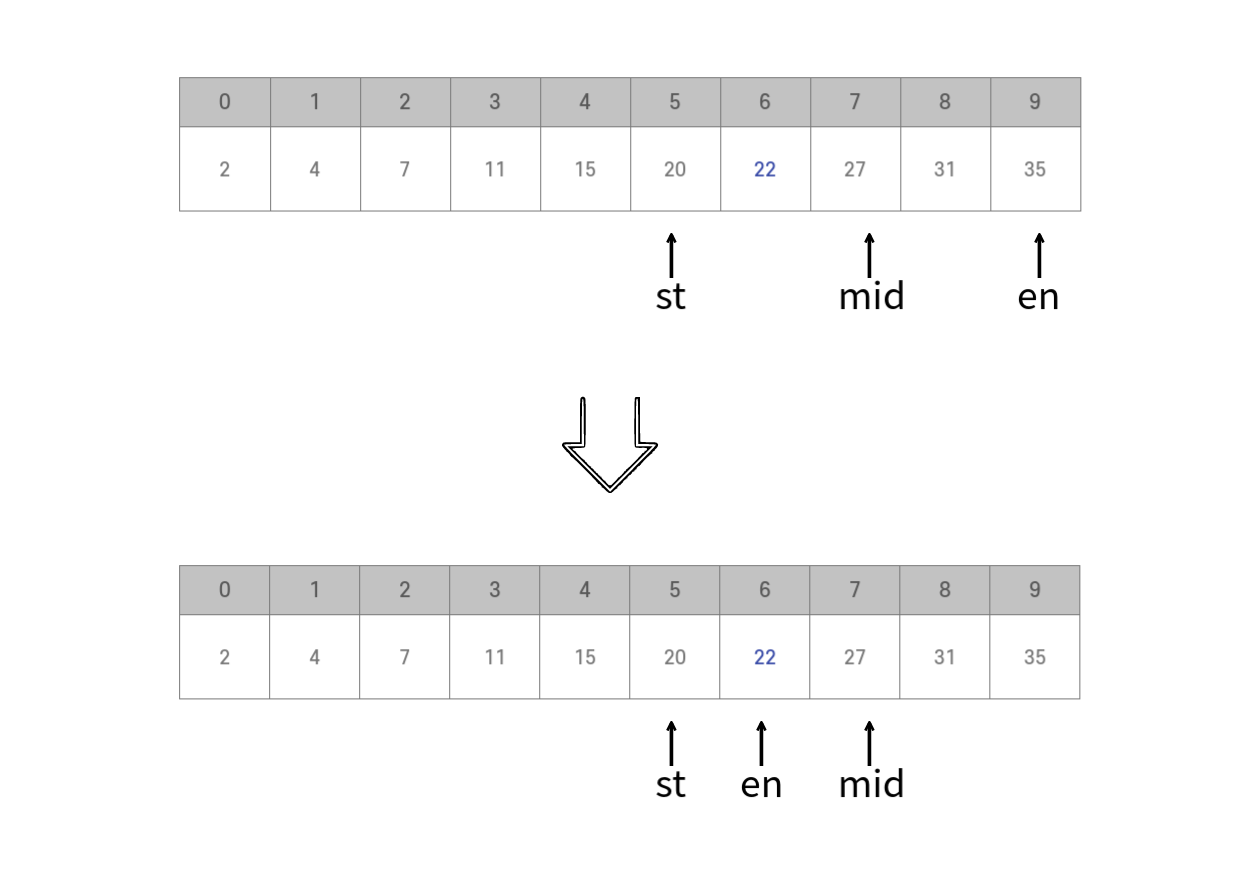mid = (5+9) / 2 = 7이 된다. A[mid] = 27 > 22 이다. 따라서 en = mid - 1 = 6으로 변경한다.
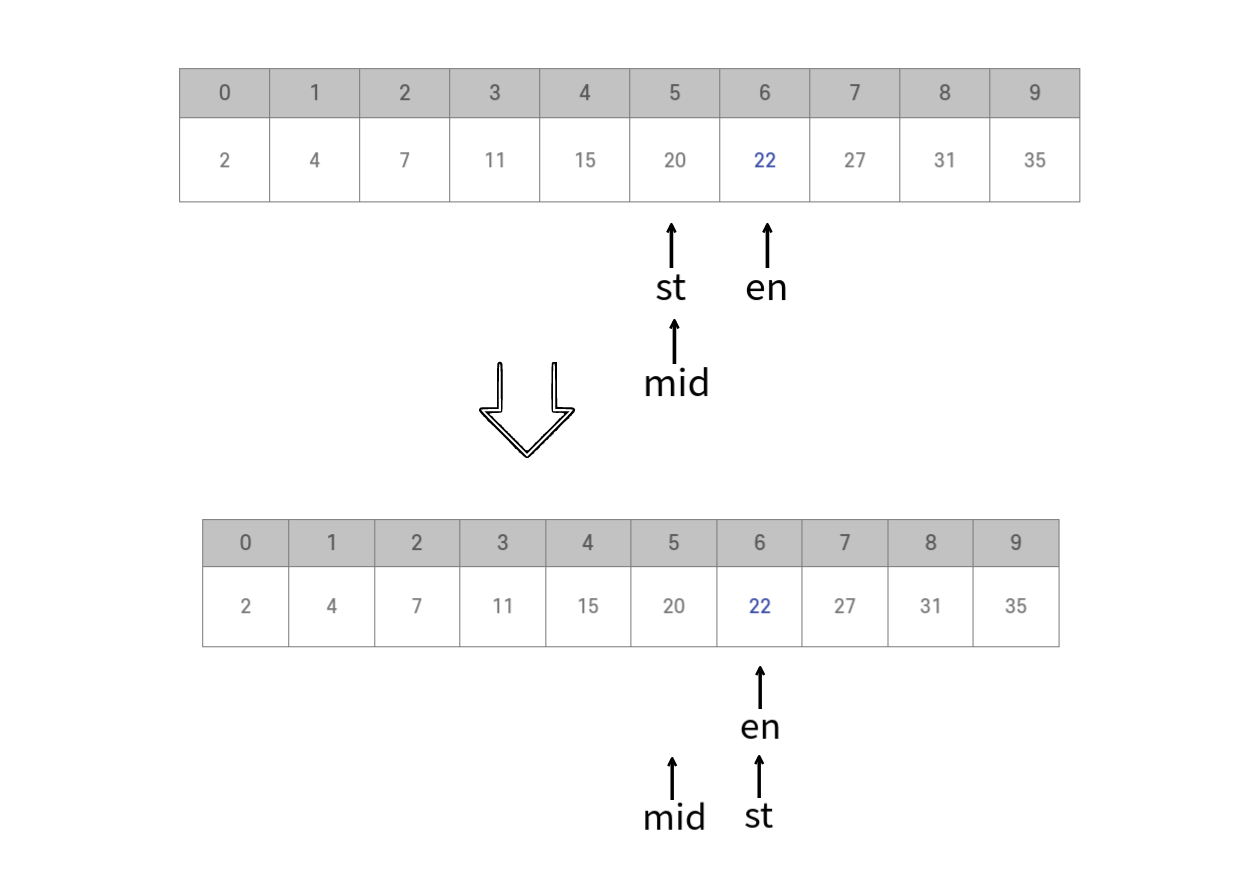mid = (5+6) / 2 = 5가 된다. A[mid] = 20 < 22 이다. 따라서 st = mid + 1 = 6으로 변경한다.

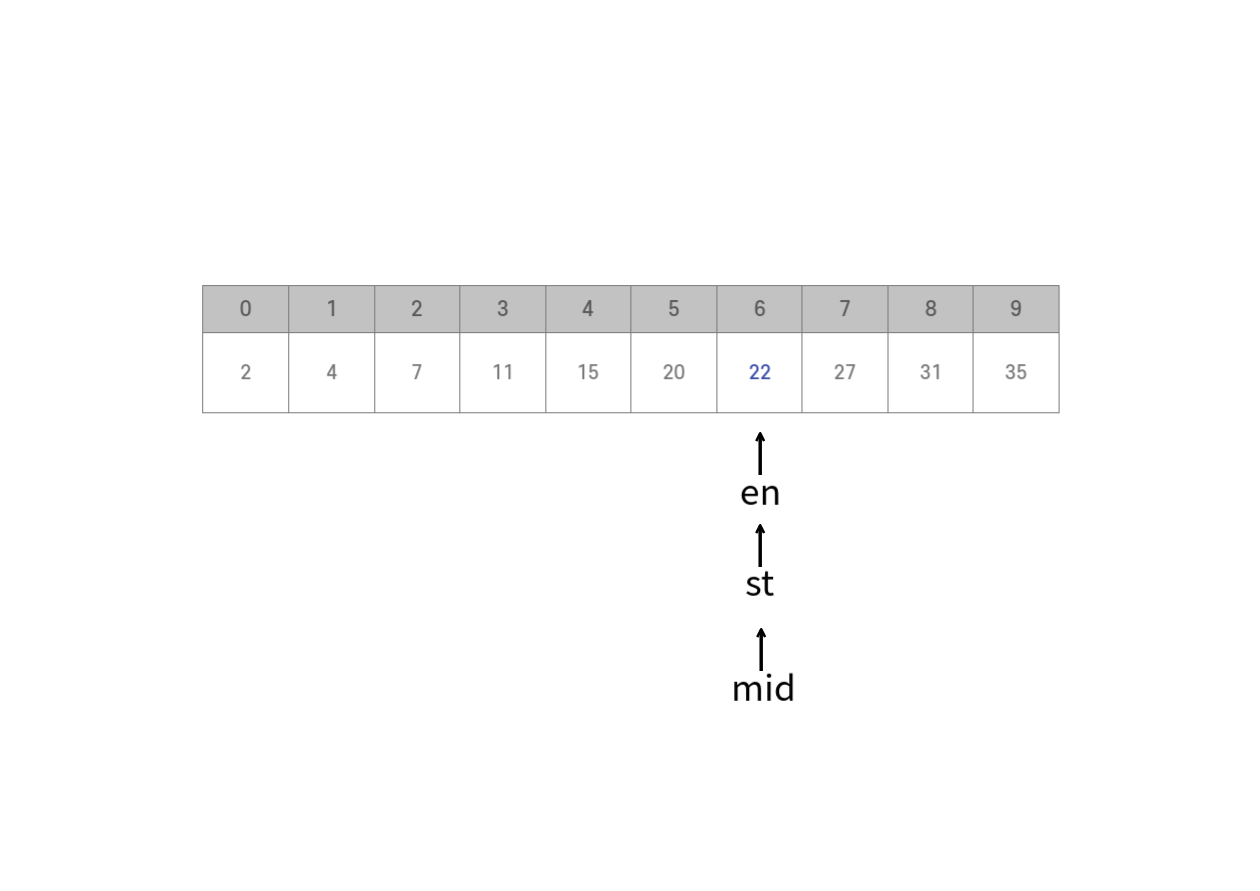mid = (6+6) / 2 = 6이 된다. A[mid] = 22 = 22 이다. 찾고자하는 값을 찾게 되었다.

st와 en이 같을 때 까지 탐색을 진행하게됐는데 여기서 st가 en보다 커져서 역전이 되는 상황이면 찾고자하는 값이 배열 안에 없음을 의미한다.
따라서 이분 탐색을 할 때 st<=en일 때만 탐색을 할 수 있도록 조건을 붙여줘야한다.

3.이분 탐색 구현 코드

#include <bits/stdc++.h>

using namespace std;

int n;
int A[100001];

int binary_search(int k)
{
    int st = 0;
    int en = n-1;
  
	
    while(st<=en)
    {
        int mid = (st+en) / 2;
        
        //A[mid] < 찾고자하는 값일 때 st = mid + 1
        if(A[mid] < k)
            st=mid+1;
        
        //A[mid] > 찾고자하는 값일 때 en = mid - 1
        else if(A[mid] > k)
            en=mid-1;
        
        //A[mid] == 찾고자하는 값일 때 반복문을 빠져나온다
        else 
            return 1;
    }
	
    //st와 en이 역전되면 값이 없는 것이므로 탐색을 중지한다
    return 0;

}

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(NULL);
    
    cin >> n;
    for(int i=0; i<n; i++)
        cin >> A[i];
   
   //배열 오름차순으로 정렬
   sort(A,A+n);

    int m,k;
    cin >> m;
    for(int i=0; i<m; i++)
    {
    	//찾고자 하는 값을 입력받고 binary_search함수를 
        //통해 값이 있는지 확인한다.
         cin >> k;
         cout << binary_search(k) << '\n';        
    }

}

위 코드는 백준 1920 수 찾기 문제를 이분 탐색을 통해 구현한 것이다.

이렇게 이분 탐색 알고리즘을 직접 구현해봤는데 사실 이분 탐색 알고리즘은 STL을 이용 할 수 있다.

4. 이분 탐색 STL

1.binary_search

binary_search(배열 시작 주소, 배열 끝 주소, 찾는 값)

정렬된 배열에서 다음과 같이 호출하면 된다.
값이 존재하면 true 없으면 false를 반환한다.

#include <bits/stdc++.h>

using namespace std;

int n;
int A[100001];

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(NULL);
    
    cin >> n;
    for(int i=0; i<n; i++)
        cin >> A[i];
   
   //배열 오름차순으로 정렬
   sort(A,A+n);

    int m,k;
    cin >> m;
    for(int i=0; i<m; i++)
    {
         cout << binary_search(A,A+n,k) << '\n';        
    }

}

아까보다 훨씬 줄어든것을 볼 수 있다.

2.lower_bound

lower_bound(배열 시작 주소, 끝 주소, 찾는 값)

정렬된 배열에서 찾는 값이 존재하는 가장 첫번째 인덱스의 주소를 반환한다.

#include <bits/stdc++.h>
using namespace std;

int n = 7;

int main(){
    int A[] = {2,3,4,7,10,10,12};
	
    //주소를 반환하므로 시작주소인 A를 빼준다
    cout << lower_bound(A,A+n,10) - A; //4
}

10은 배열에 4,5인덱스에 있다. lower_bound를 사용하면 첫번째 인덱스4의 주소를 반환한다.

3. upper_bound

upper_bound(배열 시작 주소, 끝 주소, 찾는 값)

정렬된 배열에서 찾는 값이 존재하는 마지막 인덱스 + 1의 주소를 반환한다.

#include <bits/stdc++.h>
using namespace std;

int n = 7;

int main(){
    int A[] = {2,3,4,7,10,10,12};
	
    //주소를 반환하므로 시작주소인 A를 빼준다
    cout << upper_bound(A,A+n,10) - A; //6
}

10이 위치한 마지막 인덱스는 5이다. 따라서 다음 인덱스인 인덱스6의 주소를 반환한다.

*배열에 찾는 값이 없을 때 : lower_bound , upper_bound 모두 찾는 값과 가장 가까운 큰 값의 주소를 반환한다.


#include <bits/stdc++.h>
using namespace std;

int n = 7;

int main(){
    int A[] = {2,3,4,7,10,10,12};
	
    cout << lower_bound(A,A+n,5) - A; //3
    cout << upper_bound(A,A+n,5) - A; //3
}