베이즈정리(Bayes’ Theorem)

• 통계기반, 넷플릭스 추천시스템 핵심 알고리즘 중 하나, 자율주행자동차 원래 중 하나
• 최신정보로 확률 업데이트. 즉각적인 정보에 바로 반응

조건부확률(Conditional Probability, P(A|B))

• 정보를 획득하면 확률이 달라짐.

Likelihood(가능성, 우도)

• 어떤 class안에서 어떤 현상이 관측될 확률(실제 구매의지 유무 -> 점원에게 말 걸 확률)
• class : B, ㄱB(not T), 현상 : T, ㄱT(not T) ---- 네 가지 경우의 수 나옴, 클래스가 뒤로 가야함

Posterior Probability(사후확률)

• 어떤 현상이 발견되었을 때, 그것이 특정 class에 포함될 확률
• likelihood의 정반대. P(B|T), P(ㄱB|T), P(B|ㄱT), P(ㄱB|ㄱT)
• P(B|T) = P(T|B) x P(B) / P(T)
  Posterior probability = likelihood x prior probability(사전확률) / nomalization constant
• 사후확률이 구하기 어려움. 그래서 구하기 쉬운 것들로 사후확률을 구하는 것.
• 경험, 주관, 믿음, 신뢰 등의 단어가 많이 나옴. 그것을 기반으로 사전확률 설정 가능. 예전에는 비과학적, 비수학적이라고 배제된 적도 있음.

예제1

• P(A∩B) : Joint Probability
• 말을 건다는 정보를 얻었으니까, 그것을 바탕으로 구매의지판단. 말을 걸지 않는 경우의 수는 더 이상 고려대상 아님.
  
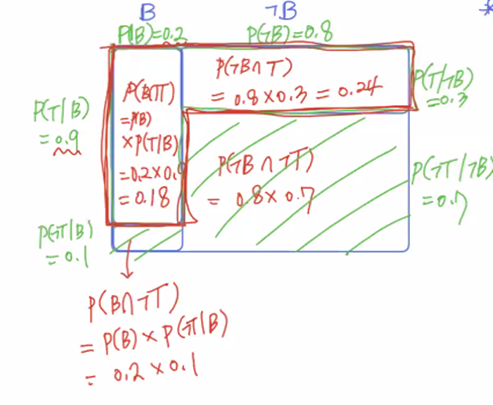
• 원래 P(B)=0.2, P(ㄱB)=0.8 -> 근데 말을 거는 상황이 관측됨 -> P(B|T)=0.43으로 업데이트됨.
• 판단의 확률이 바뀐 것임. “말을 건다”로부터 구매여부 판단. 결과로부터 원인을 판단.
• P(T) = P(B∩T)+P(ㄱB∩T)
• B인지 ㄱB인지 ---> hypothesis
• T인지 ㄱT인지 ---> evidence

예제2, 3, 4

추가설명

• 교실바닥에 긴 머리카락이 있으면 보통(likelihood) 여자의 것이라고 추측 -> likelihood기반 사고 “MLE(Maximum Likelihood Estimation)”
• 긴머리 남학생으로 이루어진 교실이라는 사전정보(prior probability)가 있으면, 긴 머리카락이 있을 때 보통(likelihood) 남자의 것이라고 추측 -> posterior기반 사고 “MAP(Maximum A Posterior)”. 이게 베이즈정리
• 새로운 확률 들어오면 베이지안 업데이트, 베이즈 갱신!
• 확률값 자체가 신뢰도
• 베이즈정리에서 확률값 “degree of belief”