코드스테이츠 17주차[FE 41기]

이동국·2022년 12월 17일
17주차코드스테이츠
0

Algorithm의 유형

알고리즘 문제를 푸는 것은 내가 생각한 문제 해결 과정을 컴퓨터의 사고로 변환하여 코드로 구현한다는 것과 같다.
코딩 테스트는 문제에 원하는 의도 및 적용해야 하는 개념이 분명하게 있고, 그것을 해결하는 것이 목표이기 때문에 알고리즘의 유형을 공부하는 것이 도움이 될 것이다.

Greedy Algorithm

탐욕 알고리즘이란?

탐욕, 말 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법이다.

탐욕 알고리즘의 문제 해결 단계

  1. 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택한다.
  2. 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사한다.
  3. 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.

예제

Greedy Algorithm - 거스름돈

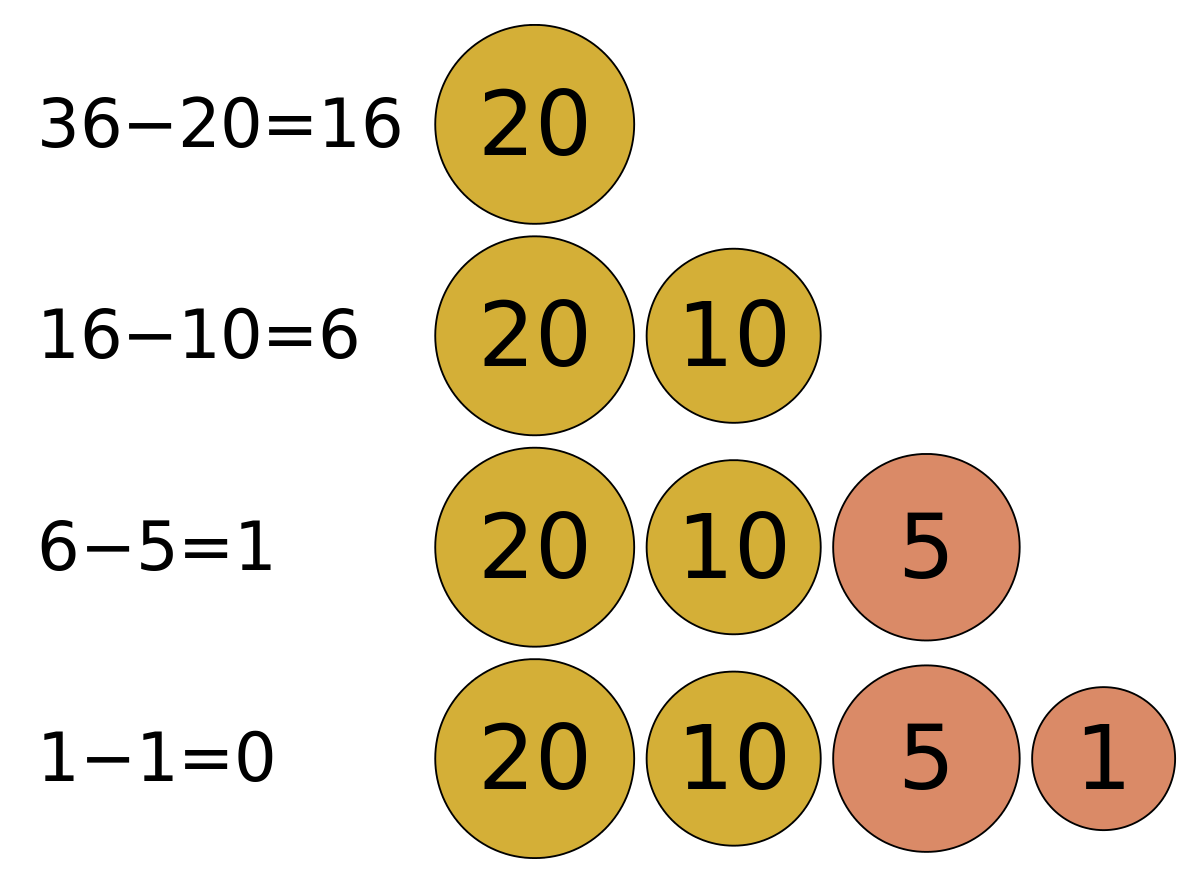
타로는 자주 JOI 잡화접에서 물건을 산다. JOI 잡화점에는 잔돈으로 500엔, 100엔, 50엔, 10엔, 5엔, 1엔이 충분히 있고, 언제나 거스름돈 개수가 가장 적게 잔돈을 준다. 타로가 JOI 잡화점에서 물건을 사고 카운터에서 1000엔 지폐를 한 장 냈을 때, 받을 잔돈에 포함된 잔돈의 개수를 구하는 프로그램을 작성하시오.

-> 즉, 언제나 거스름돈을 적게 주는 알고리즘을 구상해야한다.

예제 1
입력 : 380 / 출력 : 4

380엔을 지불해야 하면 620엔을 거스름돈으로 받아야 한다.

즉, 500엔 + 100엔 + 10엔*2 총 4개의 동전으로 거슬러 받는 것이 가장 적게 잔돈을 거슬러 받는 방법이다.

한번 로직을 작성해 보자.

function changes(input){
  
  // 1000엔 지폐를 냈고 입력값인 지불해야 할 금액을 빼주면 거스름돈이다.
  let change = Number(1000-input);
  
  // 동전의 수를 세기 위해 0을 할당해 주었다.
  let count= 0;
  
  
  // 입력값에 배열이 안들어 오기 때문에 배열 만들어 줌
  const Coins = [500, 100, 50, 10, 5, 1];
  // 코인들의 길이
  let cLength = Coins.length;

	//만든 배열의 개수만큼만 돌려줘야 함.
	for(let i = 0; i < cLength; i++){
		//거스름돈이 0원이 되면 for문을 멈춘다.
		if(change === 0) break;
		
		//거스름돈과 잔돈을 나눈 몫을 카운팅함.
		count += Math.floor(Number(change/Coins[i]));
      
		//거스름돈을 잔돈으로 나눈 나머지를 재할당
		change %= Coins[i];

	}
	
	//count를 리턴
	return count;
}

Algorithm 구현

Algorithm 구현이란?

본인이 선택한 프로그래밍 언어의 문법을 정확히 알고 있어야 하며, 문제의 조건에 전부 부합하는 코드를 실수 없이 빠르게 작성하는 것을 목표로 두는 것이다.

예제

모든 문제는 완전 탐색으로 풀 수 있다.이 방법은 굉장히 단순하고 무식하지만 "답이 무조건 있다"는 강력함이 있다.그렇지만, 문제 해결을 할 때엔 기본적으로 두 가지 규칙이 붙는다.

첫 번째, 문제를 해결할 수 있는가?

두번째, 효율적으로 동작하는가?

완전 탐색은 첫 번째 규칙을 만족시킬 수 있는 강력한 무기이지만, 두 번째 규칙은 만족할 수 없는 경우가 있기 때문에 완전 탐색은 문제를 풀 수 있는 가능한 모든 방법을 고려한 후 효율적으로 동작하는 알고리즘이 완전 탐색 밖에 없다고 판단될 때 적용할 수 있다.

완전히 탐색하는 방법에는 Brute Force(조건/반복을 사용하여 해결), 재귀, 순열, DFS/BFS 등 여러 가지가 있다. 나는 여기서 Brute Force(무차별 대입)에 대해 예시를 들어보고자 한다.

Algorithm 구현 - Brute-Force Algorithm

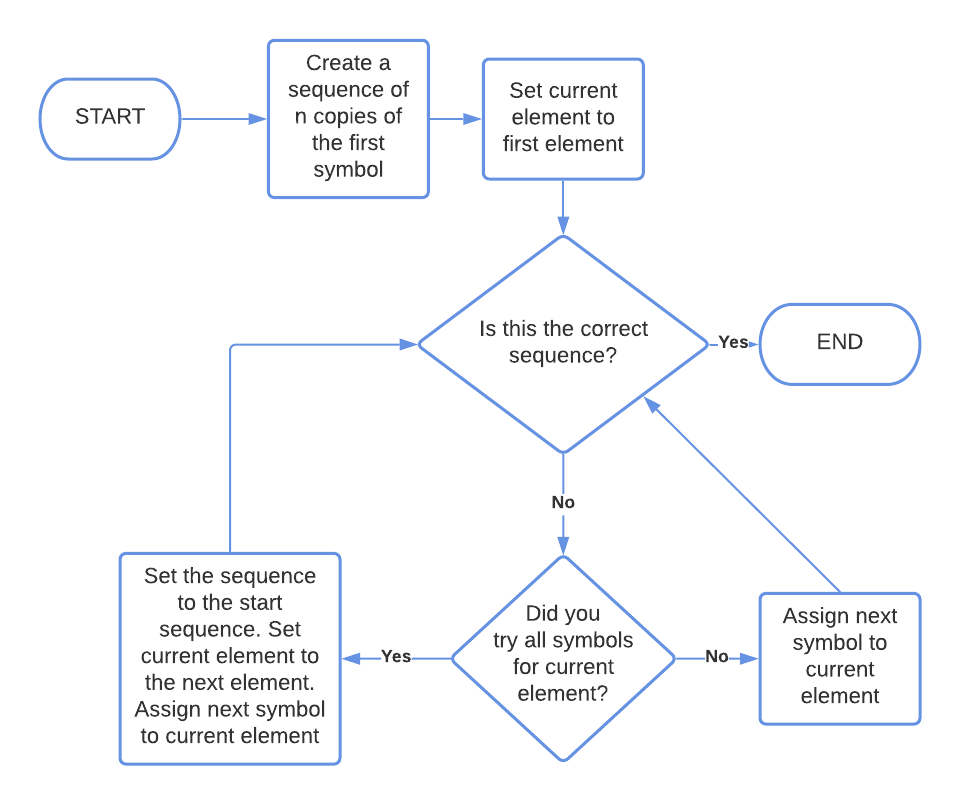
컴퓨터 과학에서 Brute Force는 시행착오 방법론을 말한다. 그리고 암호학에서도 이 용어를 사용한다고 한다. 암호학에서는 Brute Force Attack이라고 불리며 특정한 암호를 풀기 위해서 모든 값을 대입하는 방법을 말한다.

Brute Force Algorithm이란?

Brute Force Algorithm은 무차별 대입 방법을 나타내는 알고리즘이다.
순수한 컴퓨팅 성능에 의존하여 모든 가능성을 시도하여 문제를 해결하는 방법인데,
공간복잡도와 시간복잡도의 요소를 고려하지 않고 최악의 시나리오를 취하더라도 솔루션을 찾으려고 하는 방법을 의미한다.

Brute Force Algorithm은 크게 두 가지 경우에 사용된다.

  • 프로세스 속도를 높이는데 사용할 수 있는 다른 알고리즘이 없을 때
  • 문제를 해결하는 여러 솔루션이 있고 각 솔루션을 확인해야 할 때

Brute Force Algorithm의 한계

Brute Force Algorithm은 문제의 복잡도에 매우 민감한 단점을 가지고 있다. 문제가 복잡해질수록 기하급수적으로 많은 자원을 필요로 하는 비효율적인 알고리즘이 될 수 있다는 것이다.

Brute Force Algorithm의 사용

  • 순차 검색 알고리즘 (Sequential Search)

배열 안에 특정 값이 존재하는지 검색할 때 인덱스 0부터 마지막 인덱스까지 차례대로 검색한다.

function searchIndex(arr, k) {
	// 검색 키 K를 사용하여 순차 검색을 구현
	// 입력: n개의 요소를 갖는 배열 A와 검색 키 K
  // 출력: K값과 같은 요소 인덱스 또는 요소가 없을 때 -1
  
  // 현재의 배열 개수를 n에 할당
	let n = arr.length; 
  // 검색 키를 arr n인덱스에 할당
  arr[n] = k;  
   // while 반복문의 초기 값을 지정
	let i = 0;          
    // 배열의 값이 k와 같지 않을 때까지 반복
	while (arr[i] !== k) { 
       // k와 같지않을 때 i를 +1 
		i+=1      
	}
  // i가 k를 할당하기전의 배열개수보다 적다면 i를 반환
	if (i < n) {     
		return i;     
	} //-1을 반환합니다.
        else {
		return -1;     
	}
}
  • 선택 정렬 알고리즘 (Selection Sort)

전체 배열을 검색하여 현재 요소와 비교하고 컬렉션이 완전히 정렬될 때까지 현재 요소보다 더 작거나 큰 요소(오름차순 또는 내림차순에 따라)를 교환하는 정렬 알고리즘이다.

function Sorts(arr) {
  // 주어진 배열을 Sorts로 오름차순 정렬합니다.
  // 입력: 정렬 가능한 요소의 배열 A
  // 출력: 오름차순으로 정렬된 배열
  for (let i = 0; i < arr.length - 1; i++) {
  // 배열의 0번째 인덱스부터 마지막인덱스까지 반복
    
  // 현재 값 위치에 가장 작은 값을 넣음
    let min = i;
    
    // 현재 인덱스를 최소값의 인덱스를 나타내는 변수에 할당
    for (let j = i + 1; j < arr.length; j++) {
    // 현재 i에 +1을 j로 반복문을 초기화하고 i 이후의 배열요소과 비교하는 반복문을 구성
      
      if (arr[j] < arr[min]) {
      // j인덱스의 배열 값이 현재 인덱스의 배열 값보다 작다면
        min = j;
        // j 인덱스를 최소를 나타내는 인덱스로 할당
      }
    }
    // 반복문이 끝났을 때 min에는 최소값의 인덱스가 들어있음
    // i값과 최소값을 바꿔서 할당
    let temp = arr[i];
    arr[i] = arr[min];
    arr[min] = temp;
  }
	// 모든 반복문이 끝나면 정렬된 배열을 반환
  return arr;
}
  • 그 밖의 Brute Force 활용 알고리즘

버블 정렬 알고리즘 - Bubble Sort
Tree 자료 구조의 완전탐색 알고리즘 - Exhausive Search (BFS, DFS)
동적 프로그래밍 - DP(Dynamic Programing)

Dynamic Programming

Dynamic Programming(DP, 동적 계획법)이란?

주어진 문제를 여러 개의 (작은) 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결한다. 하위 문제를 계산한 뒤 그 해결책을 저장하고, 나중에 동일한 하위 문제를 만날 경우 저장된 해결책을 적용해 계산 횟수를 줄이는데 즉, 하나의 문제는 단 한 번만 풀도록 하는 알고리즘이 바로 이 다이내믹 프로그래밍이다.

다이내믹 프로그래밍 조건

  • Overlapping Sub-problems : 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제가 중복해서 발견된다.

  • Optimal Substructure : 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.

예제

Dynamic Programming - 피보나치 수열과 타일링

DP를 이용하여 피보나치 수열 문제를 해결하려고 할 때, 크게 두 가지 방식 Recursion + Memoization 과 Iteration + Tabulation 이 있다.

  • Recursion + Memoization

다이내믹 프로그래밍은 하위 문제의 해결책을 저장한 뒤, 동일한 하위 문제가 나왔을 경우 저장해놓은 해결책을 이용하는데, 이때 결과를 저장하는 방법을 Memoization이라고 한다.

function fibMemo(n, memo = []) {
// fibMemo 함수의 파라미터로 n 과 빈 배열memo 를 전달한다.
//  이 빈 배열은 하위 문제의 결괏값을 저장하는 데에 사용된다.

// n 번째 인덱스에 해당하는 피보나치 값이 저장되어 있다면, 저장되어 있는 값을 그대로 사용
    if(memo[n] !== undefined) {
			return memo[n];
		}
    if(n <= 2) {
			return 1;
		}

// 처음 계산하는 수라면 fibMemo(n-1, memo) + fibMemo(n-2, memo)를 이용하여 값을 계산하고, 그 결괏값을 res 라는 변수에 할당한다.
    let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
// 마지막으로 res 를 리턴하기 전에 memo 의 n 번째 인덱스에 res 값을 저장
// 이렇게 하면 (n+1)번째의 값을 구하고 싶을 때, n번째 값을 memo 에서 확인해 사용할 수 있다.
    memo[n] = res;

    return res;
}

Memoization을 적용한 피보나치 수열 모식도

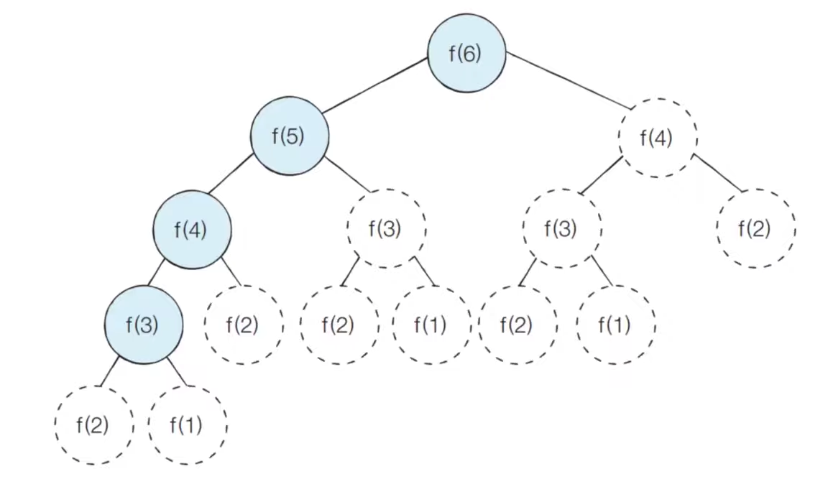
  • Iteration + Tabulation

반복문을 이용하여 다이내믹 프로그래밍을 구현하는 방식이다.
반복문을 이용한 방법은, 작은 문제에서부터 시작하여 큰 문제를 해결해 나가는 방법이기 때문에 이 방식을 Bottom-up 방식이라 부르기도 한다.

function fibTab(n) {
  
// fibTab 함수의 파라미터는 n 하나뿐이다. 만약, n 이 2와 같거나, 그 이하라면 1을 반환
//  피보나치 수열의 첫 번째와 두 번째는 1, 1이라는 것을 기억하자
    if(n <= 2) {
			return 1;
		}
// fibNum이라는 변수에 n 이 1 & 2일 때의 값을 배열을 사용해 저장해 놓자
// 피보나치 수열은 1부터 시작하지만 인덱스는 0부터 시작하기 때문에 0 번째 인덱스를 채워 줄 dummy data로 0을 삽입한다.
    let fibNum = [0, 1, 1];
  
// 2의 다음인 3부터 n까지 피보나치 수를 구하고, fibNum배열에 저장한다.
    for(let i = 3; i <= n; i++) {
        fibNum[i] = fibNum[i-1] + fibNum[i-2];
		// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
		// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다
    }
// fibNum의 n 번째 인덱스 값 을 반환
    return fibNum[n];
}

크롬 개발자 도구에서 함수 실행 시간 측정 방법

var t0 = performance.now();
fib(50); // 여기에서 함수 실행을 시켜주세요
var t1 = performance.now();
console.log("runtime: " + (t1 - t0) + 'ms')
  • 2x1 타일링

2xn 크기의 타일이 주어진다면, 2x1과 1x2 크기의 타일로 채울 수 있는 경우의 수를 모두 구해야 한다.

n = 1일 땐 경우의 수는 1 : 세로 타일 1개
n = 2일 땐 경우의 수는 2 : 세로 타일 2개 or 가로 타일 2개
n = 3일 땐 경우의 수는 3 : 세로 타일 3개 or 왼쪽 세로 타일 1개 + 가로 타일 2개 or 가로 타일 2개 + 오른쪽 세로 타일 1개

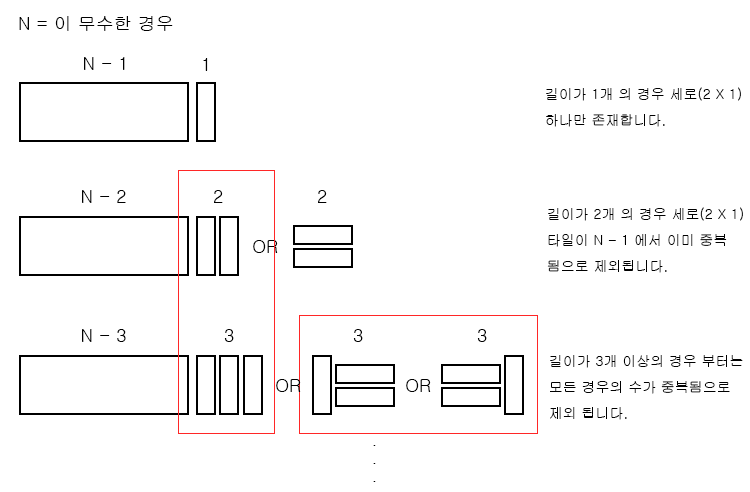
  • 2개의 타일로 빈 공간을 어떻게 채우든 상관없이, 맨 마지막 타일은 세로 타일 1개이거나 가로 타일 2개인, 2 가지 경우밖에 없다.
  • 맨 마지막 타일의 경우의 수를 제외했을 때 남는 공간의 마지막 타일도 세로 타일 1개, 혹은 가로 타일 2개인 2가지 경우밖에 없다.
  • DP 문제는 문제 속의 규칙성을 찾는 것이 키 포인트이다.

-> 세로와 가로의 마지막 타일을 제외한 나머지 공간을 채우는 경우의 수와 답이 같다.

function tile2x1(n) {
  let memo = [0, 1, 2];

  for (let i = 3; i <= n; i++) {
    memo[i] = memo[i - 1] + memo[i - 2];
  }

  return memo[n];
};
profile
이동국
이전 포스트

코드스테이츠 17주차[FE 41기]

다음 포스트

코드스테이츠 17주차[FE 41기]

0개의 댓글