Unit11 - [자료구조/알고리즘] 코딩 테스트 준비

이번시간에는 코딩 테스트에서 아주 중요한 알고리즘에 대해 학습을 하였다.
알고리즘 문제 푸는 것이 회사의 입사 조건중 하나일 수도 있기 때문에 꾸준히 공부를 하자.
Algorithm
알고리즘이란?
알고리즘은 어떤 문제를 해결하기 위해서 일련의 절차를 정의하고, 공식화한 형태로 표현한 일종의 문제의 풀이 방법, 해(解)를 의미한다. 이런 알고리즘은 프로그래밍에서는 input 값을 통해 output 값을 얻기 위한 계산 과정을 의미한다.
시간 복잡도(Time Complexity)
시간 복잡도란?
입력값과 연산 수행 시간의 상관관계를 나타내는 척도를 시간 복잡도라고 한다.
Big-O 표기법
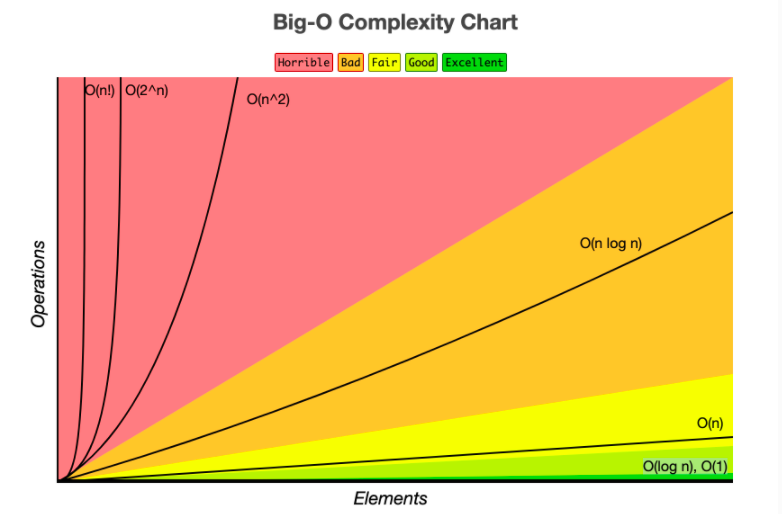
빅-오표기법은 시간 복잡도를 표시하는 방법 중 하나로, 다른 표기법 보다는 빅-오표기법을 많이 사용한다. 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가? 를 표기하는 방법이다.
- O(1)
O(1)는 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다. 즉, 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미이다.
function O_1_algorithm(str, id) {
return str[id];
}
O(n)
O(n)은 linear complexity라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
function O_n_algorithm(n) {
for (let i = 0; i < n; i++) {
// do something for 10 second
}
}O(log n)
O(log n)은 logarithmic complexity라고 부르며 Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
예를 들면 자료구조에서 배웠던 BST(Binary Search Tree)와 같다.
// 가운데 숫자를 정해 절반으로 줄여 나가며 정답을 찾는다.
int a = 0, i = N;
while (i > 0) {
a += i;
i /= 2;
}O(n2)
O(n2)은 quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
O(2n)
O(2n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
function arr(n) {
if (n <= 1) {
return 1;
}
return arr(n - 1) + arr(n - 2);
}공간 복잡도(Space Complexity)
공간 복잡도란?
공간 복잡도는 알고리즘이 수행되는 데에 필요한 메모리의 총량을 의미한다. 즉 프로그램이 필요로 하는 메모리 공간을 산출하는 것을 의미한다.
공간 복잡도 계산은 시간 복잡도 계산과 비슷하게 빅 오 (Big-O) 표기법으로 표현한다.
예시
// 공간 복잡도 O(n)
function factorial(n) {
if(n === 1) {
return n;
}
return n*factorial(n-1);
}- 보통 때의 공간 복잡도는 시간 복잡도보다 중요성이 떨어진다.
왜냐하면 시간이 적으면서 메모리까지 지수적으로 증가하는 경우는 거의 없으며 시간 내에 발생하는 메모리 문제들은 보통 알고리즘을 구현할 때에 발생하는 문제이기 때문이다.
그러므로 시간 복잡도에 맞다면 공간 복잡도도 얼추 통과하기 때문에 크게 걱정은 하지 말자.
