14-1 정렬 - (1) 선택, 삽입, 버블 정렬

• 간단하지만 비효율적인 정렬 방법
  • 삽입 정렬
  • 선택 정렬
  • 버블 정렬
• 내부 정렬
  하나의 배열에서 작업하는 경우, 모든 데이터가 주기억장치에 있음
• 외부 정렬
  배열을 위해 배열이 추가로 필요한 경우, 대부분의 데이터는 외부기억장치에있고 일부만 주기억장치에 저장된 상태에서 정렬
• 정렬 알고리즘의 안정성
  값이 똑같은 레코드들의 상대적인 위치는 정렬 후에도 바뀌지 않아야 안정적인 정렬이다.
  
  

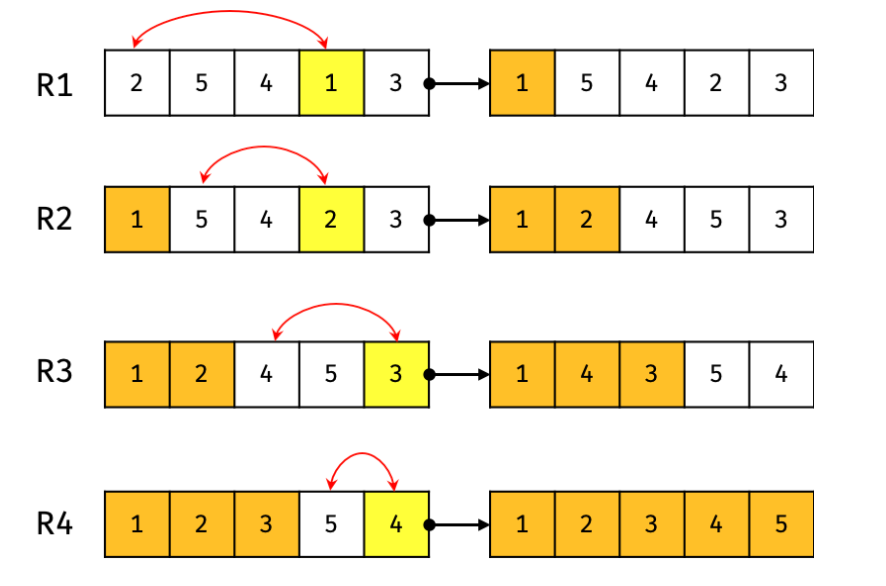
1. 선택 정렬 (Selection Sort)

• 구조: 정렬된 왼쪽 리스트와 정렬되지 않은 오른쪽 리스트를 가진다.
• 가장 작은 원소를 정렬되지 않은 부분의 맨 앞에 있는 원소와 교환하는 방식
  

void selection(vector<int>& A){
	int n = A.size();
    for(int i=0; i<n-1; i++){
    	int least = i;
        for(int j=i+1; j<n; j++){
        	if(A[least] > A[j]) least = j;
        }
        swap(A[least], A[i]);
    }
}

• 시간복잡도: O(n^2)
• 시간이 오래 걸리기 때문에 효율적인 알고리즘은 아니다.
• 안정성을 만족하지 않는다.
• 매우 간단하다.

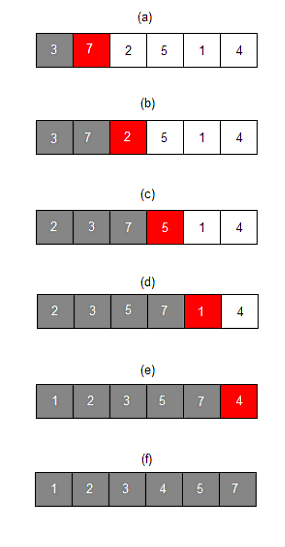
2. 삽입 정렬 (Insertion Sort)

• 두 번째 원소부터 선택한다.
• 선택한 원소보다 작은 원소가 나올 때까지 왼쪽으로 이동시킨다.
• 구조: 정렬 된 부분과 정렬 안 된 부분으로 나뉜다.
  

void insertion(vector<int>& A){
	int n = A.size();
    for(int i=1; i<n; i++){
    	int key = A[i];
        int j = i-1;
        while(A[j] > key && j >= 0){
        	A[j+1] = A[j];
            j = j-1;
        }
        A[j+1] = key;
    }
}

• 시간복잡도: O(n^2)
• 셋 중 제일 빠르다.
• 배열이 길어질수록 효율성이 떨어진다.

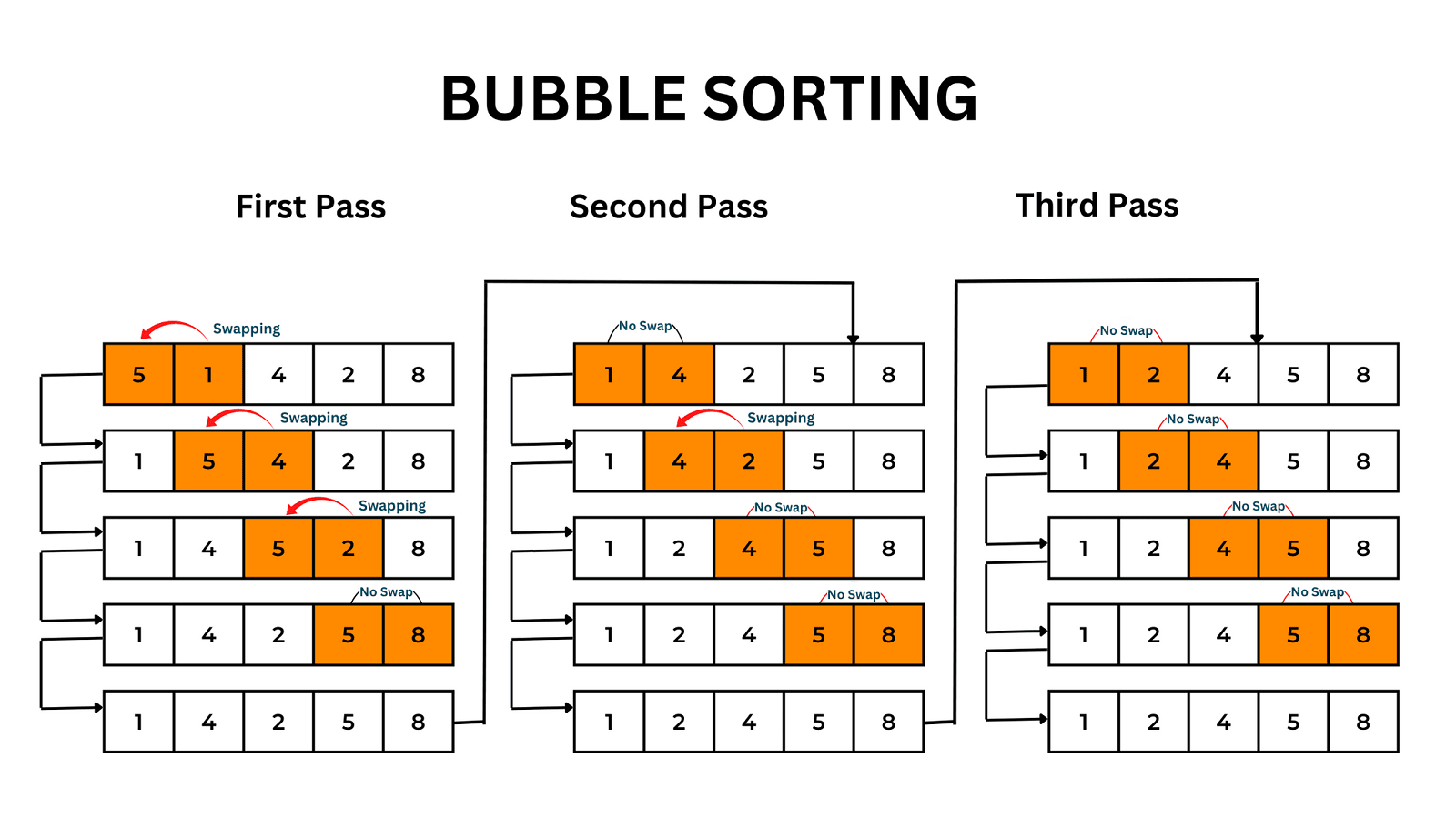
3. 버블 정렬 (Bubble Sort)

• 인접한 두 개의 데이터를 비교해서 정렬하는 방식이다.
• 배열의 첫 번째 요소로 초기화하고 인접한 두 요소를 비교하여 순서가 잘못되어 있다면 위치를 교환한다.
• 한 칸 씩 이동하면서 요소를 비교하고 교환하는 과정을 반복한다.
  

void bubble(vector<int>& A){
	int n = A.size();
    for(int i=0; i<n-1; i++){
    	for(int j=0; j<n-1-i; j++){
        	if(A[j] > A[j+1]) swap(A[j], A[j+1]);
        }
    }
}

• 시간복잡도: O(n^2)
• 정렬 알고리즘 중 가장 단순하다.
• 셋 중 제일 느리다.