
- 복잡하지만 효율적인 정렬
- 셸 정렬
- 퀵 정렬
- 합별 정렬
- 기수 정렬
1. 셸 정렬 (Shell Sort)
- 삽입 정렬을 보완한 알고리즘
- 배열을 일정한 간격(gap)으로 나누어 부분적으로 정렬한 후, 간격을 줄여가며 정렬을 반복하는 방식이다.
- 일반적으로 gap 값은 배열길이의 1/2로 설정한다.
- 정렬을 반복할 때마다 gap 값을 1/2로 줄여가는 방식이 일반적이다.
동작 과정
1. 정렬할 배열을 일정한 간격으로 나눈다.
2. 나뉜 간격에 따라 여러 개의 부분 배열을 생성한다.
3. 각 부분 배열에 대해 삽입 정렬을 수행한다.
4. 간격을 줄여가며 과정을 반복하고, 간격이 1이 될 때까지 정렬을 반복한다.
R1 : 초기 gap은 8/2=4
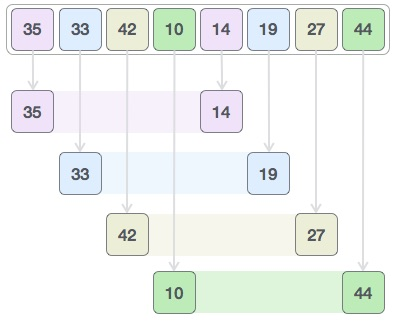
R2 : 부분 배열 정렬

R3 : gap 값은 4/2=2
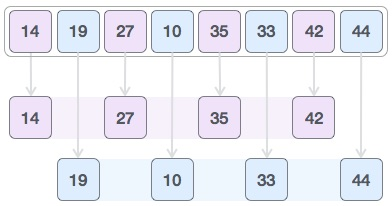
R4 : 부분 배열 정렬

R5 : gap 값은 2/2=1, 삽입 정렬을 사용하여 나머지 배열을 정렬

(이미지 출처: https://www.tutorialspoint.com/index.htm)
void shell(vector<int>& A){
int i, gap;
int n = A.size();
for(gap = n/2; gap < n; gap /=2){
if((gap % 2) == 0) gap++;
for(i=0; i<gap; i++){
gapInsrtion(A, i, n-1; gap);
}
}
}
void gapInsertion(vector<int>& A, int first, int last, int gap){
int i, j, key;
for(i = first+gap; i<=last; i += gap){
key = A[i];
for(j = i-gap; j>=first && key < A[j]; j -= gap){
A[j+gap] = A[j];
A[j] = key;
}
}
}- 시간복잡도
최선: O(n)
최악: O(n^2)
평균: O(N^1.5) - 부분 리스트가 점진적으로 정렬된 상태가 되기 때문에 삽입 정렬 속도가 증가한다.
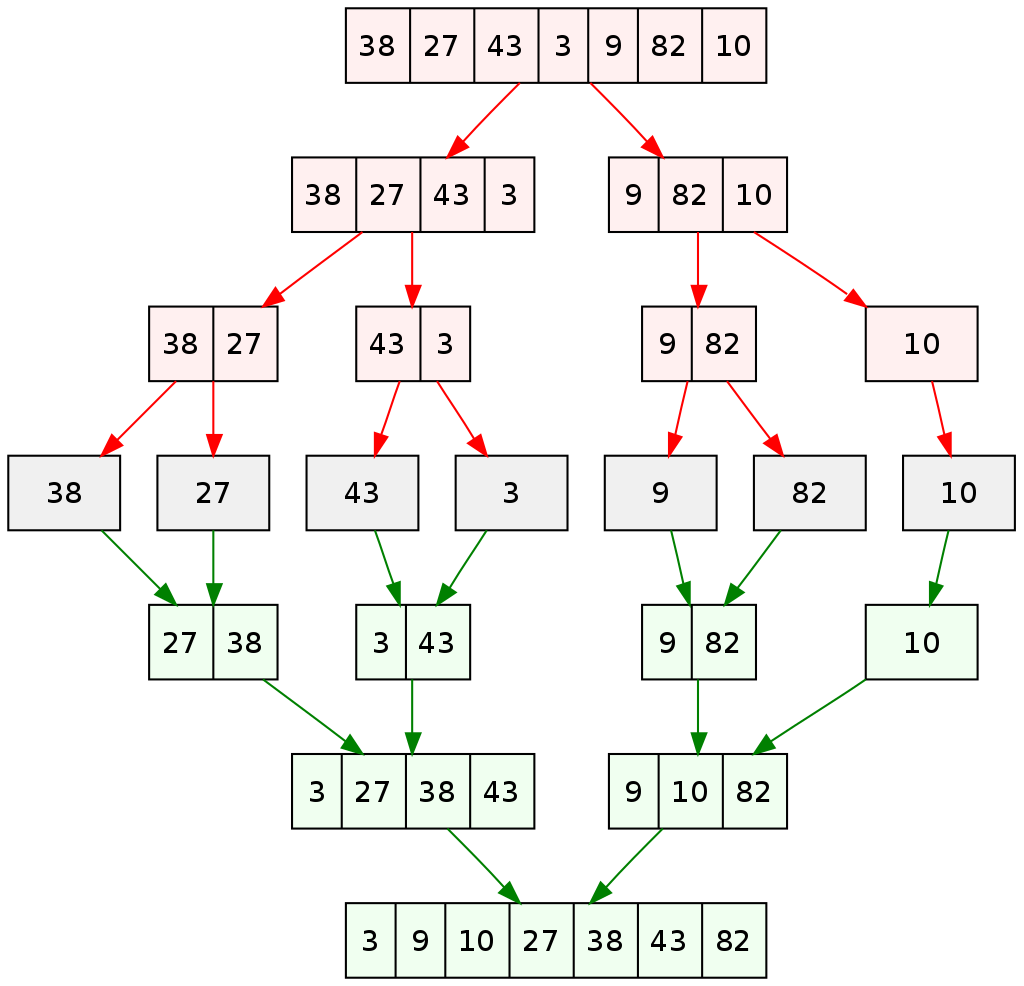
2. 합병 정렬 (Merge Sort)
- 분할 정복 방식을 기반으로 한다.
- 분할 정복 방식(divide and conquer): 문제를 보다 작은 2개의 문제로 분리하고 각 문제를 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 방법
- 분할(Divide): 리스트를 반으로 나눔 -> 리스트의 중간 지점
- 정복(Conquer): 분할된 리스트를 재귀적을 ㅗ정렬, 리스트의 크기가 충분히 작아질 때까지 반복
- 합병(Combine): 정렬된 부분 리스트를 병합하여 정렬된 하나의 리스트 생성
- 리스트를 절반으로 분할하고, 각각 재귀적으로 정렬한 후에 합병하여 정렬된 리스트를 생성하는 방식이다.
void merge(vector<int>& A, int left, int right){
vector<int> sorted(right - left + 1);
int i = left;
int j = mid+1;
int k = 0;
while(i <= mid && j <= right){
if(A[i] <= A[j]) sorted[k++] = A[i++];
else sorted[k++] = A[j++];
}
while(i <= mid) sorted[k++] = A[i++];
while(j <= right) sorted[k++] = A[j++];
for(int idk = left, k=0; idx<=num; idx++, k++){
A[idx] = sorted[k];
}
}
void ms(vector<int>& A, int left, int right){
if(left < right){
int mid = (left+right)/2
ms(A, left, mid);
ms(A, mid+1, right);
merge(A, left, mid, right);
}
}- 시간복잡도: O(nlogn)
- 입력데이터의 크기와 무관하게 일정한 성능을 보장한다.
- 효율적인 알고리즘이다.
- 데이터의 초기 분산 순서에 영향을 덜 받는다.
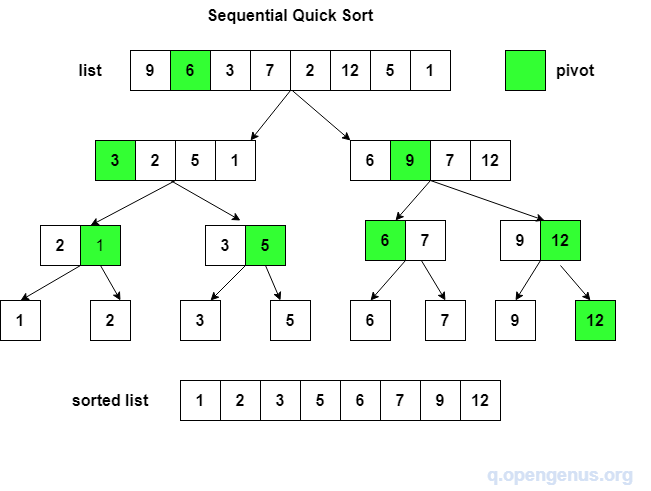
3. 퀵 정렬 (Quick Sort)
- 분할정복법 사용하며, 평균적으로 가장 빠른 정렬 방식이다.
- 분할(Divide): 입력 배열을 피벗을 중심으로 왼쪽은 피벗보다 작은 요소, 오른쪽은 피벗보다 큰 요소로 분할한다.
- 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
- 구조: 하나의 리스트를 피벗(pivot)을 기준으로 2개의 비균등한 크기로 분할하고, 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합한다.
분할 과정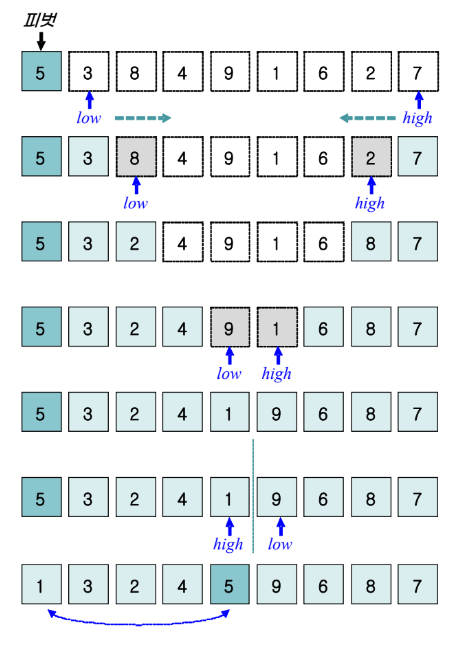
- low를 피벗보다 큰 항목까지 이동시키고 high를 피벗보다 작은 항목까지 이동시킨다.
- low와 high의 항목을 교체한다.
- 이후 low와 high가 역전되면 종료한다.
- 피벗과 high 위치의 항목을 교환한다.
퀵 정렬 전체 과정
// 배열의 left ~ right 항목들을 오름차순으로 정렬하는 함수
void quick(vector<int>& A, int left, int right){
if(left < right){
int pivot = partition(A, left, right);
quick(A, left, pivot-1);
quick(A, pivot+1, right);
}
}
// 분할 함수 partition()
int partition(vector<int>& A, int left, int right){
int low = left+1;
int high = right;
int pivot = A[left];
while(low < high){
for(; low <= right && A[low] < pivot; low++) ;
for(; high >= left && A[high] > pivot; high--) ;
if(low < high) swap(A[low], A[high]);
}
swap(A[left], A[high]);
return high;
}- 시간복잡도
최악: O(n^2)
최선: O(nlogn)
평균: O(nlogn) - 최선의 경우: 분할을 균등하게 하는 피벗을 선택하는 경우
- 최악의 경우: 이미 정렬된 배열에서 가장 작거나 가장 큰 피벗 선택하는 경우
4. 기수 정렬 (Radix Sort)
- 비교 기반 정렬 알고리즘이 아닌, 자릿수를 기준으로 정렬한다.
- 구조: 각 자릿수에 따라 여러 번의 반복을 통해 전체 원소들을 정렬한다.
동작 과정
1. 가장 작은 자릿수부터 시작하여 각 자릿수를 기준으로 그룹화한다.
2. 그룹화된 원소들을 순서대로 다시 배열에 저장한다.
3. 가장 낮은 자릿수에 대한 그룹화와 정렬이 완료되면, 다음으로 높은 자릿수로 이동하여 위의 과정을 반복한다.
- 큐로 구현한다.
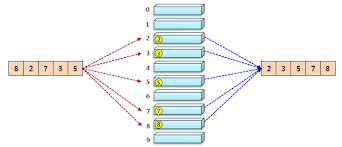
한 자릿수 기수 정렬
(8, 2, 7, 3, 5) 정렬의 경우
두 자릿수 기수 정렬
아맞다 그림
int BUCKETS = 10;
int DIGITS = 10;
void raidx(vector<int> &A){
queue<int> Q[BUCKETS];
int factor = 1;
int n = A.size();
for(int d=0; d<DIGITS; d++){
for(int i=0; i<n; i++){
Q[(A[i]/factor)%10].push(A[i]);
}
for(int b = 0, i=0; b<BUCKETS; b++){
while(!Q[b].isEmpty()){
A[i++] = Q[b].front();
Q[b].pop();
}
}
factor *= 10;
}
}- 시간복잡도: O(n)
- 메인 루프는 자릿수 d번 반복
