13-2 최단 경로 문제 - 다익스트라, 플로이드

• 최단 경로: 네트워크에서 정점u와 정점v를 연결하는 경로 중, 가중치 합이 최소가 되는 경로

1. Dijkstra 다익스트라 알고리즘

그래프의 한 노드인 시작 정점 v에서 다른 모든 정점까지의 최단 경로를 구하는 경우

• 집합 S: v에서부터의 최단경로가 이미 발견된 정점들의 집합
• dist[i] 배열: 시작 노드 v부터 i 노드까지의 최단경로 길이
  초기 값(시작 정점 v, 다른 정점들 u)
  dist[v] = 0
  dist[u] = 시작 정점 v와 u간의 가중치 값
  
  
• 가중치가 음수인 간선은 다룰 수 없다.
• 각 단계에서 거리가 가장 짧은 노드를 선택하는 탐욕적인 방식(그리디 알고리즘)

작동 과정
1. 시작 노드 정하고 모든 노드의 거리를 INF로 초기화 -> 시작 노드의 최단거리는 0으로
2. 방문하지 않는 노드 중 최단 거리가 가장 짧은 노드를 선택 (처음에는 시작 노드가)
3. 선택한 노드의 인접노드를 확인한다.
4. 인접 노드까지 바로 가는 것과 선택한 노드를 거쳐서 인접 노드로 가는 것 중 거리가 더 짧은 것으로 최단 거리를 업데이트한다.
5. 모든 노드가 방문 되면 알고리즘 종료, 아니라면 2번으로 돌아가서 반복한다.

시각화

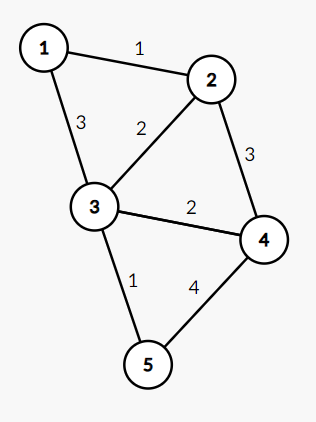
1. 초기 세팅
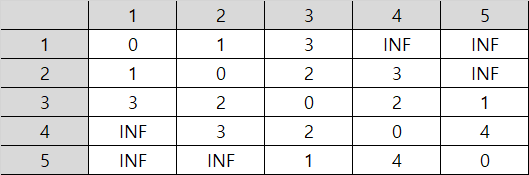표는 특정 행에서 열로 가는 가중치를 의미한다.


2. 시작 노드로 노드 1 선택

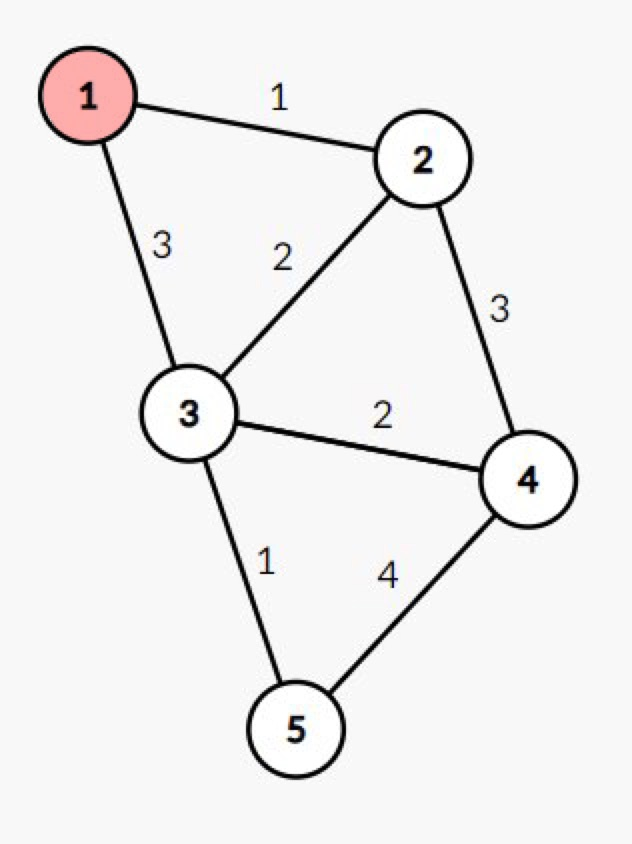
3. 방문하지 않은 노드 중 비용이 가장 작은 노드 2 방문

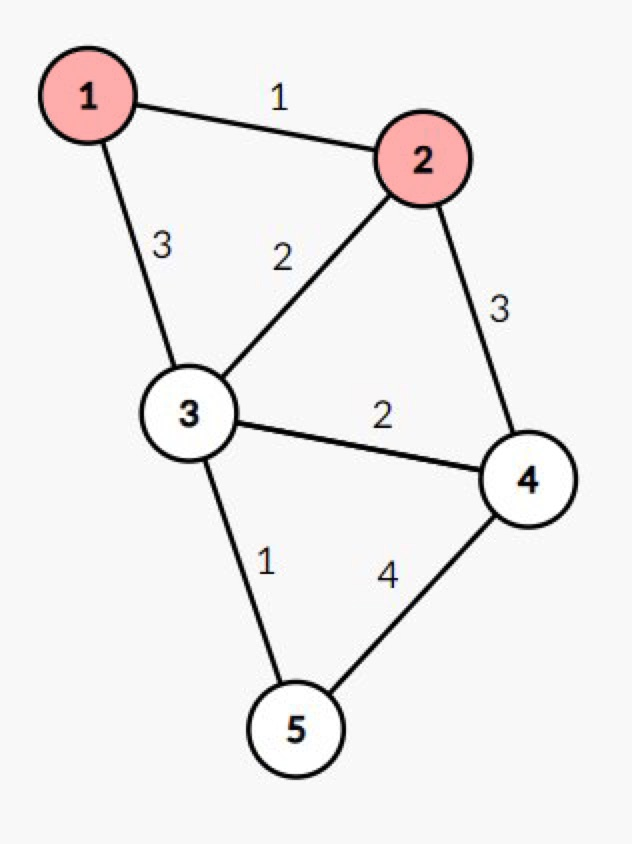
4. 노드 3 방문

   

   

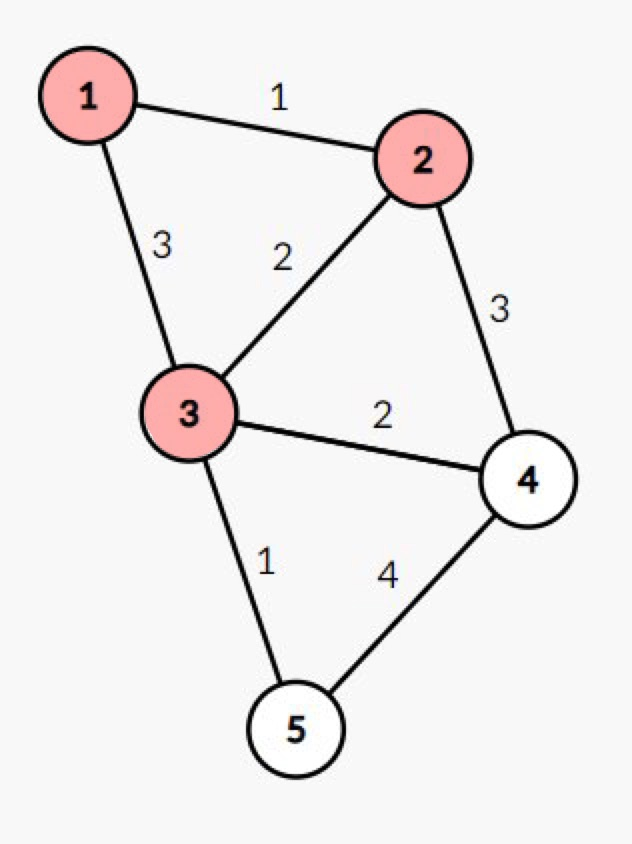
5. 노드 5 방문 -> 최소 비용 갱신 발생X
   
   

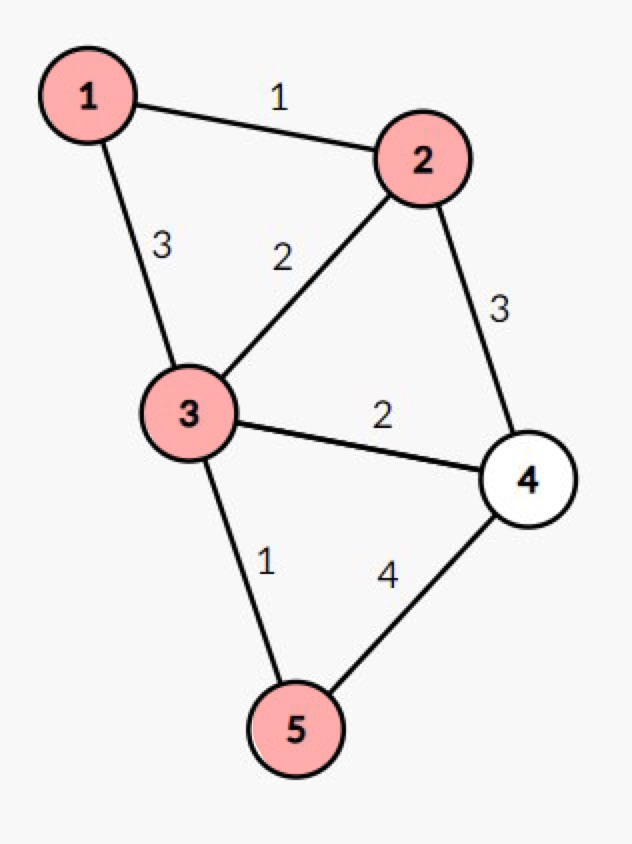
6. 노드 4 방문 -> 최종 배열 생성
   

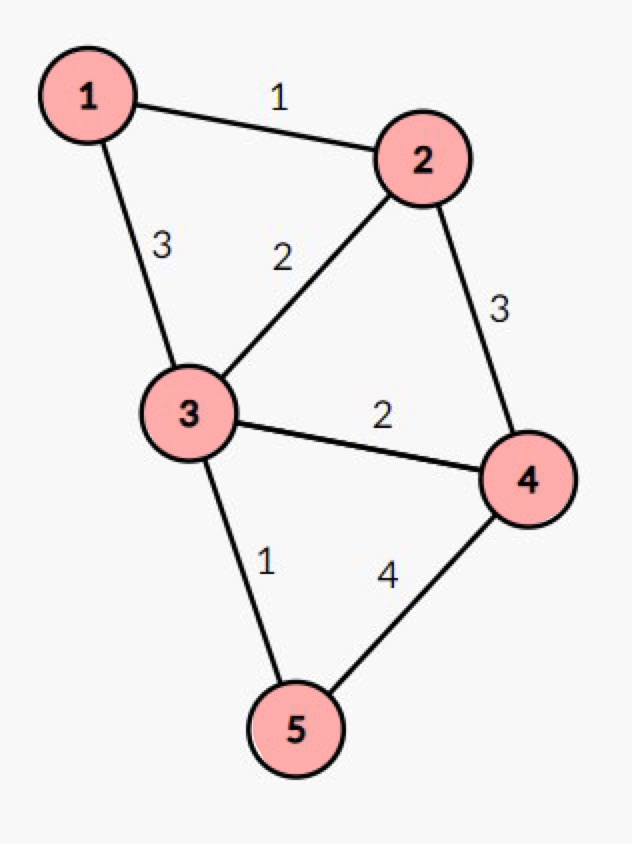
dijkstra(int start){
	int dist[start] = 0;
    for(int i=0; i<n; i++){
    	int cur = -1;
        int minD = INF;
        for(int j=1; j<=n; j++){
        	if(!visited[j] && (minD > dist[j])){
           		minD = dist[j];
                cur = j;
           }
        }
        visited[j] = true;
        for(int j=0; j<a[cur].size(); i++){
        	int near = a[cur][j].first;
            int nearD = a[cur][j].second;
            if(dist[near] > nearD + dist[j]){
            	dist[near] = nearD + dist[j];
            }
        }
    }
}

2. Floyd 플로이드 알고리즘

• 그래프의 모든 정점 쌍 사이의 최단 경로를 구하는 알고리즘
• 음수 가중치를 가지는 간선이 있어도 동작할 수 있다.
  • 모든 정점에서 모든 정점으로의 최단 경로를 구하고 싶을 때 사용한다.
• 거쳐가는 정점을 기준으로 최단거리를 구하는 것을 의미한다.
  • 모든 노드 쌍(i, j)에 대하여 "노드 k를 거쳐가는 경로"와 "노드 k를 거치지 않는 경로" 중에서 더 짧은 경로를 선택한다.
• 음수 사이클은 처리할 수 없다.

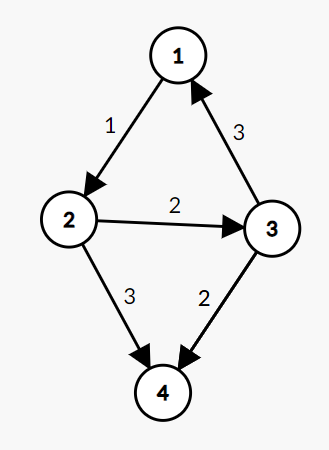
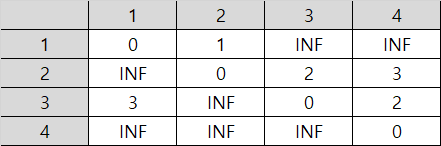
1. 초기 세팅

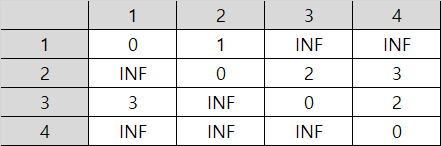
(1) 노드 1을 거쳐가는 경우

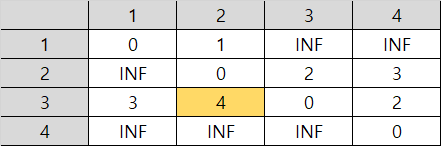
(2) 노드 2를 거쳐가는 경우

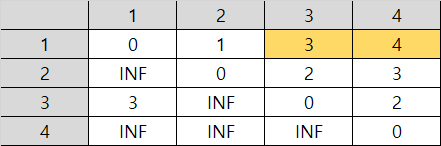
(3) 노드 3을 거쳐가는 경우

• 2 -> 4의 경우, 노드 3을 거쳐가는 경로와 노드 3을 거치지 않는 경로 중 더 짧은 경로를 선택해야 한다.
  • 노드 3을 거치는 경우: 2 + 2 = 4
  • 노드 3을 거치지 않는 경우: 3

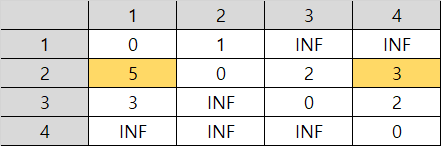
(4) 노드 4를 거쳐가는 경우

작동 과정
1. 그래프의 인접행렬을 INF로 초기화하고, 정점에서 자기 자신으로의 거리는 0으로 초기화한다.
2. 방문하지 않은 노드 중 최단 거리인 노드를 선택한다.
3. 모든 정점을 순회하며 거쳐가는 정점을 선택: 이 정점을 k라고 한다.
4. 경로(i, j)에 대해, 최단거리(i, j)와 (i, k)+(k, j) 중 더 짧은 경로로 갱신한다.
5. 모든 정점을 거쳐가며 2~3단계를 반복한다.

void floyd(){
	vector<vector<int>> d(num, vector<int>(num));

	for(int i=0; i<number; i++){
		for(int j=0; j<number; j++){
    		d[i][j] = a[i][j];
    	}
	}

	for(int k=0; k<number; k++){
		for(int i=0; i<number; i++){
    		for(int j=0; j<number; j++){
        		if(d[i][k] + d[k][j] < d[i][j])
            		d[i][j] = d[i][k] + d[k][j];
        	] 
    	}
	}
}