13-1 최소비용신장트리

1. 신장 트리(Spanning Tree)

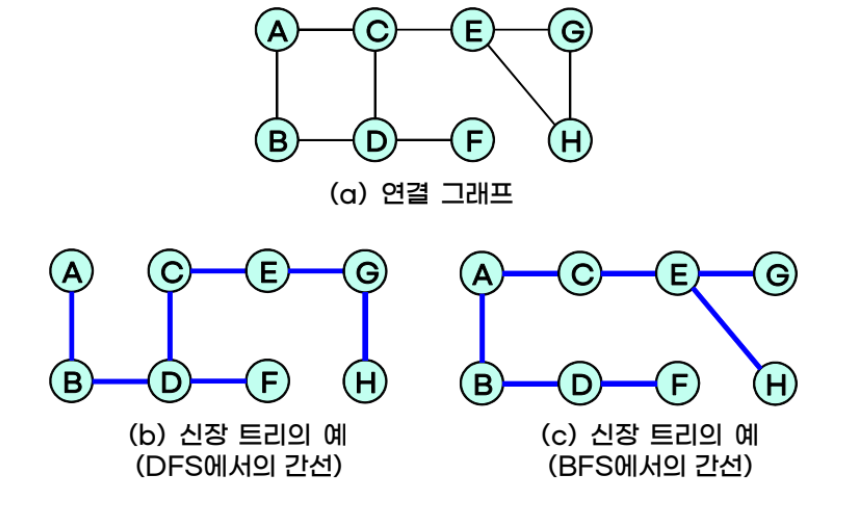
• 신장 트리: 그래프의 모든 정점을 포함하면서 사이클이 없는 부분 그래프
• n-1개의 간선만 사용

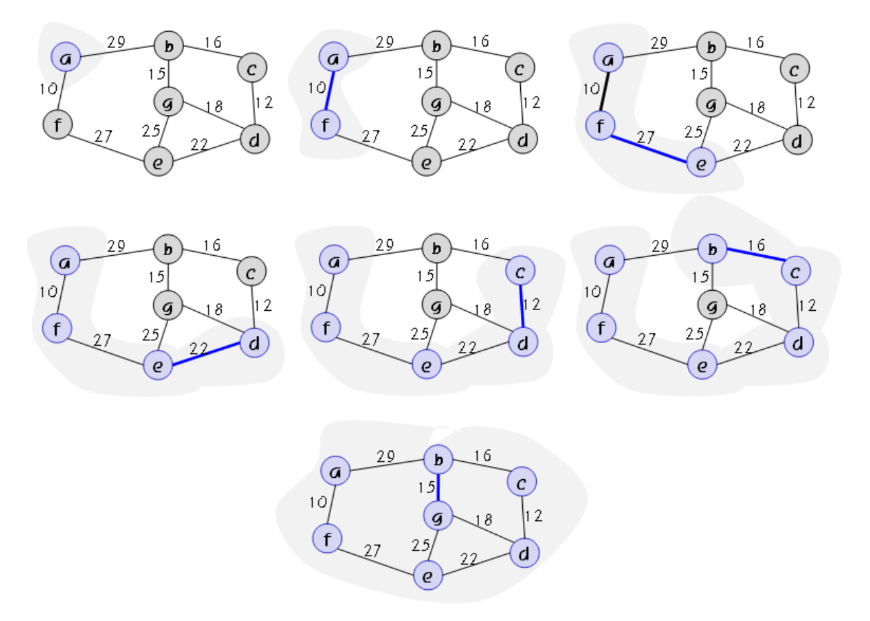
2. 최소 비용 신장 트리(Minimum Spanning Tree, MST)

• 최소 비용 신장 트리(Minimum Spanning Tree, MST): 간선들의 가중치를 합한 값이 최소가 되는 신장 트리
• n-1개의 간선만 사용한다.
• 사이클이 없다.

3. kruskal의 MST 알고리즘

• greedy method: 각 단계에서 최선의 답을 선택하는 과정을 반복하는 알고리즘 설계 기법, 항상 최적의 해답을 주는지 검증이 필요하다.
• Kruskal의 MST 알고리즘은 최적의 해답임이 증명되었다.

1. 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬
2. 가중치가 가장 작은 간선 e를 선택(이후 정렬된 순서대로 간선 선택)
3. e를 신장 트리에 넣을 경우 사이클이 생기면 삽입X, 2번으로 이동
4. 사이클이 생기지 않으면 e를 최소 신장 트리에 삽입
5. n-1개의 간선이 될 때까지 2번으로 이동

4. union - find 알고리즘(사이클 검사)

• union - find 알고리즘: Disjoint Set(서로소 집합)을 표현하는 자료구조
• union: 두 정점이 속한 각각의 집합을 하나의 집합으로 묶는 연산
• find: 정점이 어떤 집합에 속해 있는지 찾는 연산
  

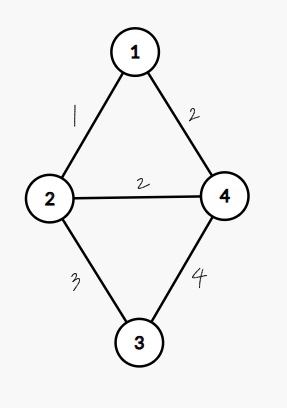
1. 부모 테이블 초기화
   parent 배열은 각 정점의 root node(부모)를 표현한 배열이다.
   초기에는 자기 자신이 루트노드가 되게 초기화 되어 있는 상태이다.(parent[i] = i)
   parent 배열: {1}, {2}, {3}, {4}

   1	2	3	4
   1	2	3	4

2. 가중치의 오름차순 정렬 순서대로 간선 1-2를 선택한다.
   정점1과 정점2를 연결하면서 Union 연산에 의해 두 집합이 합쳐진다.
   이 때, Union 연산으로 두 정점의 루트 노드(부모)가 다른지 판단하고 다르다면 합친다.
   해당 집합 내에서 제일 작은 숫자가 그 집합에서의 루트 노드가 되게끔 가정한다.

   따라서 parent[2] = 1이 된다.

   parent 배열: {1, 2}, {3}, {4}

   1	2	3	4
   1	1	3	4

3. 간선 1-4를 선택한다.
   정점1의 루트노드는 1이고 정점4의 루트노드는 4이다. 두 정점의 루트 노드가 다르기 때문에 Union 연산으로 합칠 수 있다.

   따라서 parent[4] = 1이 된다.

   parent 배열: {1, 2, 4}, {3}

   1	2	3	4
   1	1	3	1

4. 간선 2-4 선택
   정점2의 루트노드는 1이고 정점4의 루트노드도 1이다. 두 정점의 루트 노드가 같기 때문에 합칠 수 없다.(사이클을 형성하기 때문)
   -> 사이클이 생기는지 확인하는 방법: 각 노드의 루트 노드가 동일한지 아닌지를 보면 알 수 있다.

// 정점 집합 클래스(Union-Find 연산)
class VertexSets{
    int parent[MAX_VERTICES];
    int size;
public:
    VertexSets(int nSets){
        size = nSets;
        for(int i=0; i<nSets; i++) parent[i] = -1;
    }

    bool IsRoot(int i) {return parent[i] < 0;}

    int findSet(int vertex){
        int id = vertex;
        while(!IsRoot(id)) id = parent[id];
        return id;
    }

    void unionSets(int s1, int s2){
        parent[s2] = s1;
        size--;
    }

    void print(int i){
        cout << parent[i] << endl;
    }
};

5. prim의 MST 알고리즘

• 처음에는 시작 정점만이 신장 트리 집합에 포함된다.
• 시작 정점과 인접한 정점 중 최저 간선으로 연결된 정점을 선택하여 신장 트리 집합에 추가하는 과정을 n-1개의 간선을 가질 때까지 반복한다.

1. 그래프에서 시작 정점을 선택하여 초기 트리를 만든다.
2. 현재 트리의 정점들과 인접한 정점들 중에서 간선의 가중치가 가장 작은 정점 v를 선택한다.
3. 이 정점 v와 이 때의 간선을 트리에 추가한다.
4. 모든 정점이 삽입될 때까지 2번으로 이동한다.