Fly me to the Alpha Centauri

문제

풀이

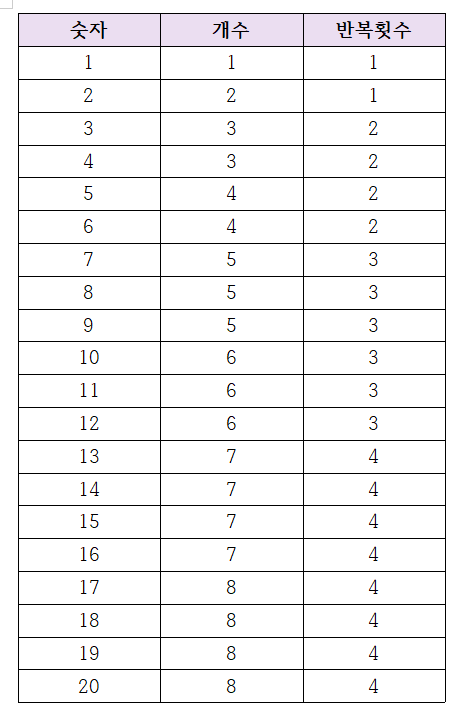
위에 표는 규칙을 찾아낸 표이다.
ex)
0~1일 때 => 1
0~2일 때 => 11
0~3일 때 => 111
...
0~20일 때 => 12344321

이제 2^31인 큰 수의 값을 구하기 위해선 1~2^31까지 하나씩 찾는 것이 아니라 규칙을 찾아야 한다.
반복 횟수에서 해답을 찾을 수 있었다.

반복횟수 1 => 2에서 끝남 +2 증가
반복횟수 2 => 6에서 끝남 +4 증가
반복횟수 3 => 12에서 끝남 +6 증가
반복횟수 4 => 20에서 끝남 +8 증가

즉 19라면 반복횟수가 4라는 것을 확인 후 7인지, 8인지 여부를 확인하면 된다.
7인지, 8인지 판단할 때에는 반복횟수 마지막은 20이라는 것을 알기 때문에
7,8 경계값 20-4 = 16 보다 크면 8, 작으면 7이 되는 것이다.

for test_case in range(1):
    n = int(sys.stdin.readline())

    for _ in range(n):
        x, y = map(int, sys.stdin.readline().split())

        dist = y - x

        hap = 0
        p = 1
        while True:
            if hap >= dist:
                break
            hap += 2*p
            p += 1

        if hap - (p - 1) + 1 <= dist:
            print((p - 1)* 2)
        else:
            print(((p - 1)* 2) - 1)

hap은 반복횟수 마지막번호를 의미한다.
p는 인덱스 번호이다. 이것을 통해서 2,4,6,8씩 증가할 수 있다.
만약 dist가 5라고 가정하자
반복횟수 마지막번호가 6일 때 break될 것이다.
즉 반복횟수 마지막번호가 6을 의미하는 것은
3또는 4라는 의미이다.
이제 3, 4사이에서 구하는 조건을 구해야 한다.
p = 3이기 때문에 6 - (3-1) + 1 보다 크면 4
그렇지 않으면 3이다.