최소비용 구하기

문제

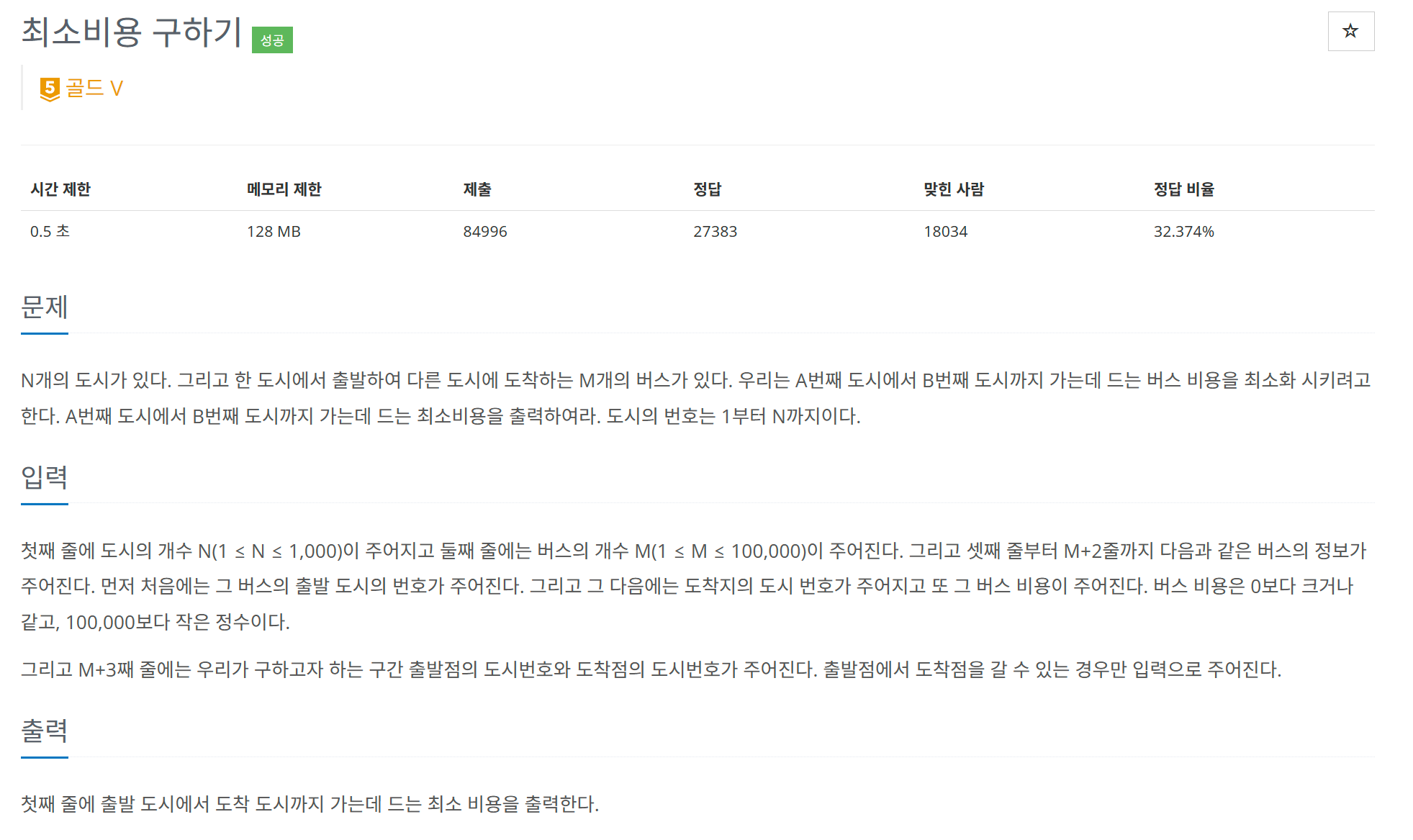
풀이

이 문제는 다익스트라를 사용해서 풀면 된다.

그래프로 나타내보자

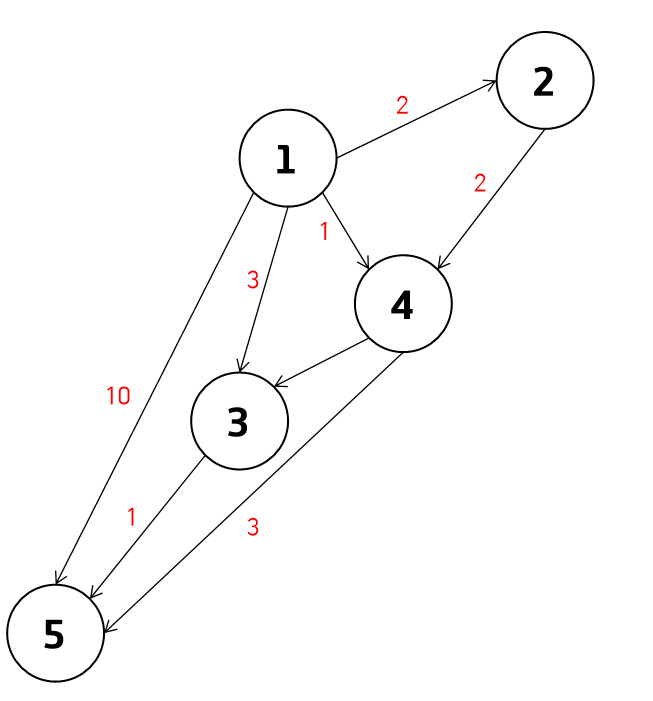
이것을 표로 나타낼 수 있다.

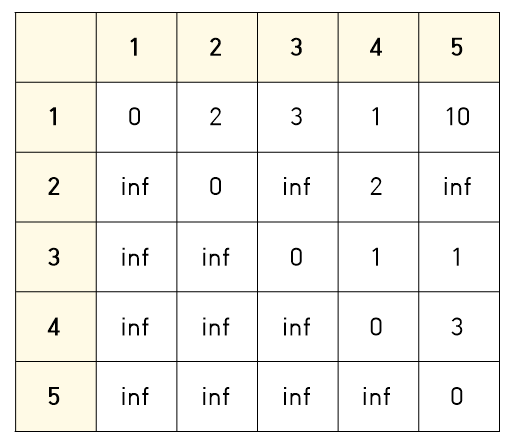
각 노드별 최소 경로를 inf로 초기화 한다.

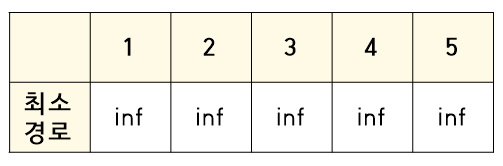
1. 시작경로는 1이다.

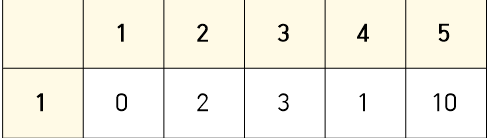
즉 1에서 2 => 2
1에서 3 => 3
1에서 4 => 1
1에서 5 => 10 이다.
현재 최소경로는 전부 inf이므로 전부 다 작으므로 해당 값으로 업데이트 해준다.

또한 1은 방문했다는 표시를 해준다.

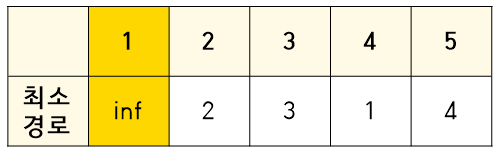
2. 현재 최소 경로는 1이므로 4번 째 노드를 확인해본다.
4번 노드에서 갈 수 있는 경로를 확인해보자

4에서 5 => 3 만큼 갈 수 있다.
기존에 1 -> 5에 최소 경로는 10 이였다.
하지만 1 -> 4 -> 5로 가면 4다. 업데이트 시켜준다.

또한 4는 방문했다는 표시를 해준다.

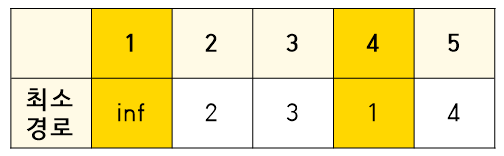
3. 방문하지 않는 노드중 현재 최소 경로는 2이므로 2번 째 노드를 확인해본다.
2번 노드에서 갈 수 있는 경로를 확인해보자

기존 최소 경로 1 -> 4 = 1
현재 경로 1 -> 2 -> 4 = 4

그대로 변경없이 진행한다.

또한 2는 방문했다는 표시를 해준다.

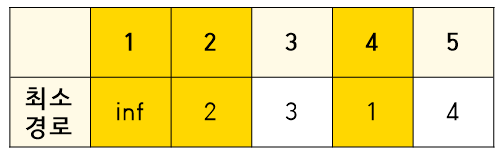
4. 방문하지 않는 노드중 현재 최소 경로는 3이므로 3번 째 노드를 확인해본다.
3번 노드에서 갈 수 있는 경로를 확인해보자

기존 최소 경로에서 3을 거쳐서 갈 수 있는 경로는 4, 5이다.
하지만 4같은 경우 1이므로 그대로 가져간다.

또한 5도
3 + 1 = 4 똑같으므로 그대로 4로 진행한다.
또한 3은 방문했다는 표시를 해준다.

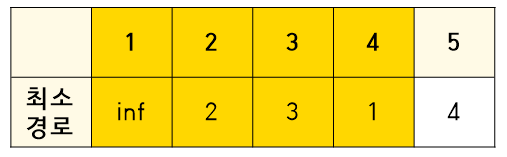
5. 마지막 노드를 확인한다.
5번 노드에서 갈 수 있는 경로를 확인해보자

아무것도 없으므로
최종적으로

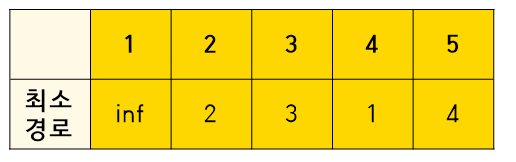
이렇게 된다.

코드

for test_case in range(1):
    n = int(sys.stdin.readline())
    m = int(sys.stdin.readline())

    graph = [[float("inf") for _ in range(n + 1)] for _ in range(n + 1)]

    for _ in range(m):
        start, end, cost = map(int, sys.stdin.readline().split())
        graph[start][end] = min(graph[start][end], cost)

    for i in range(n + 1):
        graph[i][i] = -1

    distance = [float("inf") for _ in range(n + 1)]
    visited = [False for _ in range(n + 1)]

    def dijkstra(start):
        q = []
        heappush(q, (0, start))
        distance[start] = 0

        while q:
            cur_dist, cur_node = heappop(q)
            visited[cur_node] = True

            if distance[cur_node] < cur_dist:
                continue

            for new_node in range(1, n + 1):
                if visited[new_node] or cur_node == new_node or graph[cur_node][new_node] == float('inf'):
                    continue

                if distance[new_node] > cur_dist + graph[cur_node][new_node]:
                    distance[new_node] = cur_dist + graph[cur_node][new_node]
                    heappush(q, (cur_dist + graph[cur_node][new_node], new_node))

    start, end = map(int, sys.stdin.readline().split())
    dijkstra(start)
    print(distance[end])

여기서 핵심은

graph[start][end] = min(graph[start][end], cost)
이부분이다.
input값으로 주어질 때 중복될 수도 있기 때문에 최소값을 저장해준다.
이 부분 때문에 많은 시간이 걸렸던 문제이다.

import sys

from heapq import heappush, heappop

for test_case in range(1):
    n = int(sys.stdin.readline())
    m = int(sys.stdin.readline())

    graph = [[] for _ in range(n + 1)]

    for _ in range(m):
        start, end, cost = map(int, sys.stdin.readline().split())
        graph[start].append((end, cost))

    distance = [float("inf") for _ in range(n + 1)]
    visited = [False for _ in range(n + 1)]

    def dijkstra(start):
        q = []
        heappush(q, (0, start))
        distance[start] = 0

        while q:
            cur_dist, cur_node = heappop(q)
            visited[cur_node] = True

            if distance[cur_node] < cur_dist:
                continue

            for new_node, new_dist in graph[cur_node]:
                if visited[new_node]:
                    continue

                if distance[new_node] > cur_dist + new_dist:
                    distance[new_node] = cur_dist + new_dist
                    heappush(q, (cur_dist + new_dist, new_node))

    start, end = map(int, sys.stdin.readline().split())
    dijkstra(start)
    print(distance[end])

이차원 배열을 만들고 하는 것이 아니라
경로만 이차원 배열에 저장하는 방식으로도 가능하다.