평범한 배낭

문제

knapsack알고리즘

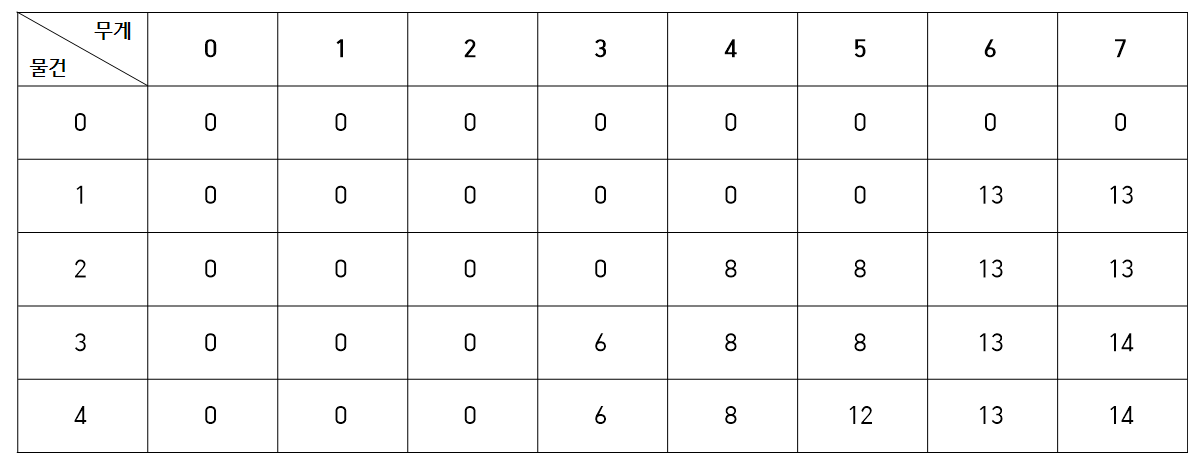
물건 1. 무게: 6, 가치: 13일 때
가방 무게가 1~5까지일 때에는 6을 담을 수 없으므로 0이 된다.
하지만 6, 7에서는 6을 담을 수 있다.
dp[1][6] = dp[0][0] + 13 이라고 할 수 있다. (이전 최대값)
dp[1][7] = dp[0][1] + 13 이라고 할 수 있다.

물건 2. 무게: 4, 가치: 8일 때
가방 무게가 1~3까지일 때에는 4를 담을 수 없으므로 0이 된다.
하지만 4, 5, 6, 7에서는 4를 담을 수 있다.
dp[2][4] = dp[1][0] + 8
dp[2][5] = dp[1][1] + 8
dp[2][6] = max(dp[1][2] + 8, dp[1][6])
dp[2][7] = max(dp[1][3] + 8, dp[1][7])

물건 3. 무게: 3, 가치: 6일 때
가방 무게가 1~2일 때까지는 3을 다음 수 없으므로 0이 된다.
반면에 3, 4, 5, 6, 7에서는 3을 담을 수 있다.
dp[3][3] = dp[2][0] + 6
dp[3][4] = max(dp[2][4], dp[2][1] + 6)
dp[3][5] = max(dp[2][5], dp[2][2] + 6)
dp[3][6] = max(dp[2][6], dp[2][3] + 6)
dp[3][7] = max(dp[2][7], dp[2][4] + 6)

풀이

...
이런식으로 점화식을 도출하면 다음과 같다.
dp[i][j] = max(dp[i-1][j - cur_weight] + cur_value, dp[i-1][j])

for test_case in range(1):
    n, k = map(int, sys.stdin.readline().split())

    arr = []
    for _ in range(n):
        arr.append(list(map(int, sys.stdin.readline().split())))

    dp = [[0 for i in range(k + 1)] for j in range(n + 1)]

    for i in range(1, n + 1):
        for j in range(1, k + 1):
            cur_weight, cur_value = arr[i-1][0], arr[i-1][1]

            if cur_weight <= j:
                dp[i][j] = max(dp[i-1][j - cur_weight] + cur_value, dp[i-1][j])
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])

    print(dp[n][k])