이번 포스팅은 "1부. 머신러닝 레벨업의 지름길. 캐글" 파트에서 "04장. 데이터를 한눈에: 주요 시각화 그래프"를 알아보는 파트의 정리를 마치고, 2부로 들어가 본격적으로 06장부터 진행되는 머신러닝 경진대회를 진행하기 전에, "05장. 다시 살펴보는 머신러닝 주요 개념" 파트에서 하이퍼파라미터 최적화 부분의 "베이지안 최적회" 파트의 내용을 간단하게 정리하고 넘어가겠다.

평소 하이퍼파라미터 최적화 기법인 "그리드 서치"나 "랜덤 서치"는 사용해 보았지만, 베이지안 최적화 기법은 구현해보거나 관련 라이브러리를 사용해본 적이 없어 이번 포스팅에서 경험하고 본격적인 경진대회 포스팅으로 넘어가려고 한다.

베이지안 최적화(Bayesian Optimization)

What is Bayesian Optimzation?

"베이지안 최적화(baysian optimization)"

• 사전 정보를 바탕으로 최적 하이퍼파라미터 값을 확률적으로 추정하며 탐색하는 기법이다.
• 그리드 서치나 랜덤 서치보다 최적 하이퍼파라미터를 더 빠르고 효율적으로 찾아준다.
• 코드도 직관적이라 사용하기 편하다.

bayes_opt 패키지를 통해 베이지안 최적화를 구현할 수 있다.

bayes_opt 패키지 기준으로 베이지안 최적화를 수행하는 절차는 다음과 같다.

베이지안 최적화 수행 절차 (설명)

1. 하이퍼파라미터 탐색 범위 설정

- 최적 값을 찾고 싶은 하이퍼파라미터의 범위 설정

2. 평가지표 계산 함수(성능 평가 함수) 정의

- 탐색하려는 하이퍼파라미터를 인수로 받아 평가 지표 값을 계산해주는 함수를 정의

3. BayesianOptimization 객체 생성

- `bayes_opt` 패키지의 `BayesianOptimization` 객체를 생성한다.

- 객체 생성 시 '평가지표 계산 함수'와 '하이퍼파라미터 탐색 범위'를 입력받는다.

4. 베이지안 최적화 수행

- (3)번에서 생성한 BayesianOptimization 객체의 maximaize() 메서드를 호출한다.

- 하이퍼파라미터 범위 내 값을 평가지표 계산 함수에 전달하면서 평가지표 값을 구한다.

- 평가지표 값이 가장 좋았을 때의 하이퍼파라미터 값을 최적 하이퍼파라미터로 간주한다.

위 수행 절차를 기반으로 간단한 예제를 통해 베이지안 최적화를 수행해보겠다.

베이지안 최적화 수행 절차 (예시)

이 예제에서 탐색할 하이퍼파라미터는 x와 y가 되겠다. 탐색 범위는 딕셔너리 형태로 지정한다.

1) 하이퍼파라미터 탐색 범위 설정

Code

# 하이퍼파라미터 범위(딕셔너리 형태)
param_bounds = {'x': (-1, 5),
                'y': (0, 4)}

딕셔너리의 key에 하이퍼파라미터 이름을, value에 하이퍼라미터 범위(튜플 형태)를 지정하면 된다.
하이퍼파라미터 x범위가 $(-1, 5)$라면, $-1$ ~ $5$ 사이의 값을 탐색하겠다는 뜻이다.

2) 평가지표 계산 함수 정의

Code

# 임의로 만들어본 평가지표 계산 함수
def eval_function(x, y):
    return -x ** 2 - (y - 2) ** 2 + 10

베이지안 최적화는 평가지표 계산 함수로 구한 평가점수를 최대화 하는 방향으로 하이퍼파라미터를 탐색한다.

평가 점수가 가장 큰 값일 때의 하이퍼파라미터를 최적 하이퍼파라미터로 간주한다.

하지만 이는 실제 최적 하이퍼파라미터가 아닐 수 있으며, 최적일 가능성이 높은 하이퍼파라미터이다.

3) 베이지안 최적화 객체 생성

다음으로는 BayesianOptimization()으로 베이지안 최적화 객체를 생성한다.

Code

from bayes_opt import BayesianOptimization

# 베이지안 최적화 객체 생성
optimizer = BayesianOptimization(f=eval_function,
                                 pbounds=param_bounds,
                                 random_state=0)

중요한 생성 파라미터

• f => '최대화하려는 평가지표 계산 함수' 전달
• pbounds => '하이퍼파라미터 범위' 전달

random_seed을 설정하여 시드 값 고정 시, 다음번에 실행할 때도 동일한 결과 값을 얻을 수 있다.

4) 최적화 수행

Code

# 베이지안 최적화 수행
optimizer.maximize(init_points=2, n_iter=10)

중요한 생성 파라미터

• init_points : 랜덤 탐색을 수행할 스텝 횟수(랜덤 탐색은 공간을 다양화함으로써 최적화에 도움을 줄 수 있음)
• n_iter : 베이지안 최적화를 수행할 스텝 횟수(스텝 횟수가 많을수록 최적 값을 찾을 가능성이 높다)

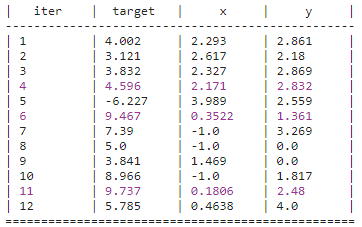
Result

실행 결과에서 총 스텝 횟수(12)는 init_points(2)와 n_iter(10)을 합칭 횟수이다.

중간 중간 결과가 빨갛게 출력되는 것은 평가 함수 점수가 기존 최댓값을 갱신했다는 뜻이다.

따라서 빨간 결과 중 가장 마지막 스텝의 평가점수가 전체에서 최대가 되는 값이다.

이 결과에서는 11번째 스텝의 평가점수가 전체에서 최대가 되는 값, 즉 베이지안 최적화로 찾은 최적 하이퍼파라미터이다.
($x=0.181$, $y=2.48$)

이 값은 베이지안 최적화 객체의 max에 저장되어 있다.

5) 최적화 결과 확인

Code

# 평가점수가 최대일 때 타깃 x, y값 출력
optimizer.max

Result

Wrap Up

이번 포스팅에서는 기존에 다루어보지 않았던 하이퍼파라미터 최적화 기법인 베이지안 최적화 기법에대해서 사용해보았다.

이제 다음 포스팅부터는 처음 경진대회를 진행하는 포스팅이니만큼, 접속 방법이나 세부 메뉴에 대해서도 다루어보면서 인터페이스도 익혀볼 예정이다.

이후에는 캐글에 있는 노트북을 리팩터링 하면서 EDA부터 제출까지 진행하는 과정의 포스팅이 이루어질 예정이다.