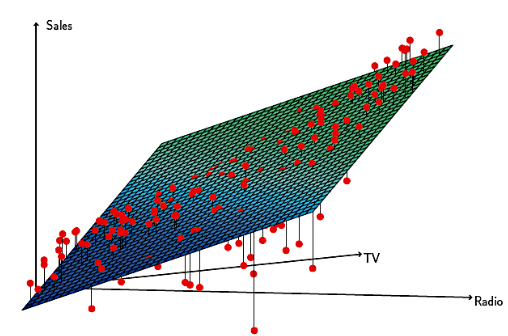
회귀(Regression) : 주어진 데이터(X)와 찾고자하는 값(y) 사이의 관계를 찾는 방법 /
찾고자하는 값 ( y = traget value)를 예측하는 방법.
01. Definition
Linear Regression : 로 표시되는 선형식으로 x와 y 사이의 관계를 찾는 모델(W가 여러 개 이면 다중선형회귀) → 근본 모델이므로, 정확히 알아야 딥러닝(perceptron) 이해 easy/ 다른 모델들의 근간이 되는 모델.
- 의 식을 자세히 들여다보면, 다음과 같이 표시 가능.
→
- 처음에는 랜덤 값을 가지는 W들을 가지고 예측 수행.
→ 임의의 값 . 이 예측값은 (정말 운이 좋은 경우를 제외하고) 실제 값과 많이 동떨어져있음.
→ 예측 값이 실제 값과 가까워지려면 파라미터들(, )을 업데이트 해야함.
02. Loss Function
회귀에서 가장 많이 사용하는 loss function: MSE(Mean Squared Error)
→ SSE는 어쩔 수 없이 데이터가 늘어나면 에러가 더 늘어남
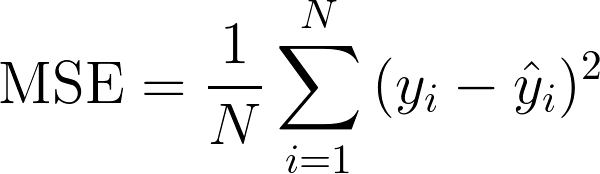
- 모델의 예측값 이 실제값 에 가까워지게 학습.(전체적으로 loss의 평균이 작아지는 방향으로 학습 진행)
< Loss Space >
Q1. Loss가 0이되면 어떤 의미인가?
A1. y =
Q2. Loss가 0이 되는 지점을 찾을 수 있을까요? 데이터에의해결정됨
A2. 알 수 없다.(데이터에 의해 결정)
Q3. Loss가 최소가 되는 지점을 어떻게 찾을까요?
A3. 1. analytic solution(수학적으로): resource cost 무지막지하게 증가할 수 있음.
2. practical solution: 경사하강법
< Loss Function Optimization >
Gradient Desecent Algorithm을 이용하여 w,b 업데이트(loss가 최소가 되는)
-
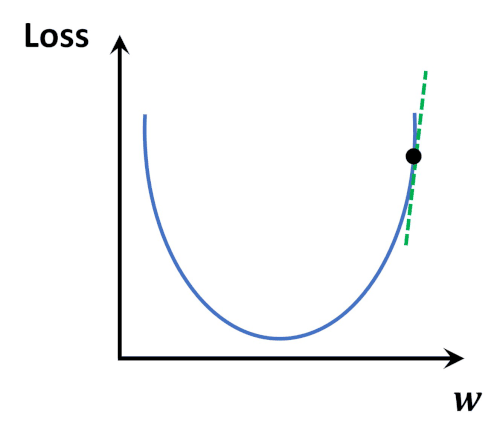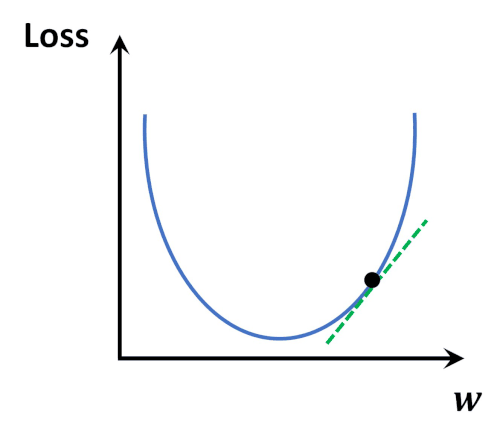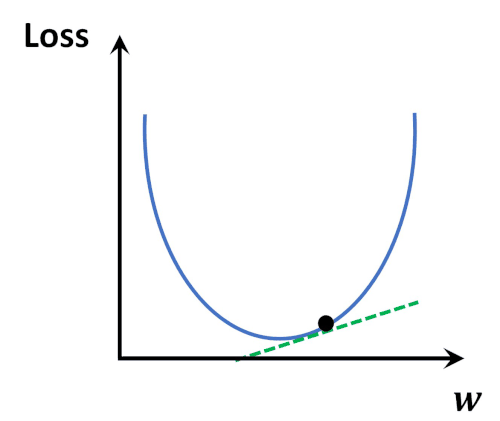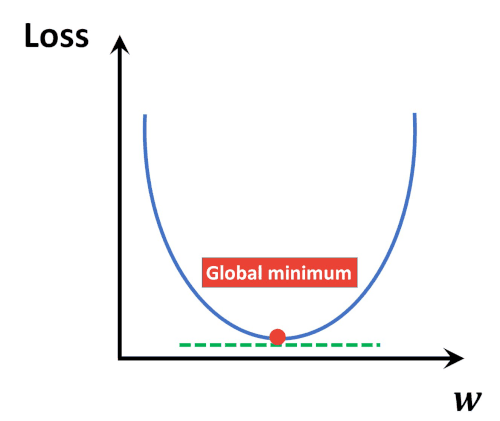
Loss function(MSE)은 convex(볼록)함수, 때문에 경사하강법으로 항상 optimal solution을 찾을 수 있음.
→ why?
볼록 함수는 전역 최솟값(global minimum)이 하나만 존재하며 로컬 최솟값(local minimum)이 없음.
경사 하강법을 사용하더라도 수렴 시 전역 최적점에 도달 가능. -
다시 말해, 주어진 데이터에 대해 선형 회귀 모델을 훈련시키고자 할 때, MSE를 최소화하는 가중치(weight)와 편향(bias)을 찾을 수 있음. 경사 하강법을 사용하면 MSE를 최소화하는 방향으로 모델 파라미터를 업데이트하면서 점차적으로 최적의 파라미터 값을 찾아갈 수 있음.
- 따라서 선형 회귀는 주어진 데이터에 대해 최적의 선형 모델을 찾을 수 있는 도구이며, 그 최적 모델은 MSE를 최소화하는 파라미터로 정의됨.
03. Conclusion
< 장점 >
- 통계적으로 설명 가능한 이론이 많음(설명도구가 많음)
- interpretavility : 수식 자체가 선형식이기 때문에 직접 계산하여 예측값 왜 나오는지 설명 가능.
- Linear model 자체가 가지는 simplicity 때문에 general한 모델 많이 나옴
→ 때로는 복잡한 모델들 보다 예측성능 더 뛰어남.
