Lasso, Ridge : Linear Regression이 고차원 공간에 overfitting(너무 많은 feature가 있는 경우 전부다 고려해서 학습이 잘 안됨, generalization 잘 안됨)이 쉽게 되는 문제를 해결한 기법.
Lasso
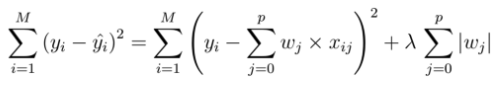
- weight의 L1 term(L1 정규화)을 Loss function에 더해줌.(람다는 hyperparameter)
- 람다는 규제강도
- 추가한 항(L1 term)도 gradient descent algorithm의 최적화 대상에 속함
- L1 term을 제약조건이라 부르고 또는
Regulization term이라고 함. - L1 정규화는 가중치의 절댓값을 패널티로 부과하여 가중치를 희소하게 만듬. 이는 불필요한 특성(feature)을 제거하고 모델의 복잡성을 줄이는 효과
- L1 정규화는 변수 선택(feature selection) 효과를 가지며, 중요한 특성에 대응하는 가중치를 강조하고 나머지 가중치를 0으로 만들 수 있음.
Ridge
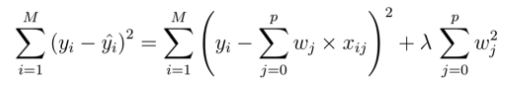
- weight의 L2 term(L2 정규화)을 Loss function에 더해줌.(람다는 hyperparameter)
- 추가한 항(L2 term)도 gradient descent algorithm의 최적화 대상에 속함
- L2 term을 제약조건이라 부르고 또는
Regulization term이라고 함. - L2 정규화는 가중치의 크기를 패널티로 부과하여 가중치를 일반화시킴. 이는 가중치 값이 작아지도록 유도하며, 모든 가중치가 균등하게 작아지도록 함.
- L2 정규화는 오버피팅을 줄이고 모델의 일반화 능력을 향상시키는 데 도움.
정리
-
Lasso나 Rigde를 적용했을 때, 성능이 향상된다면 Linear Regression 모델에 사용되는 feature vector가 차원을 줄일 필요가 있다는 얘기가 됨.
→ feature selection이 성능 향상을 가져온다
-
Regulization을 할 때, 가중치를 사용하는 방식을
weight decay라고 함. -
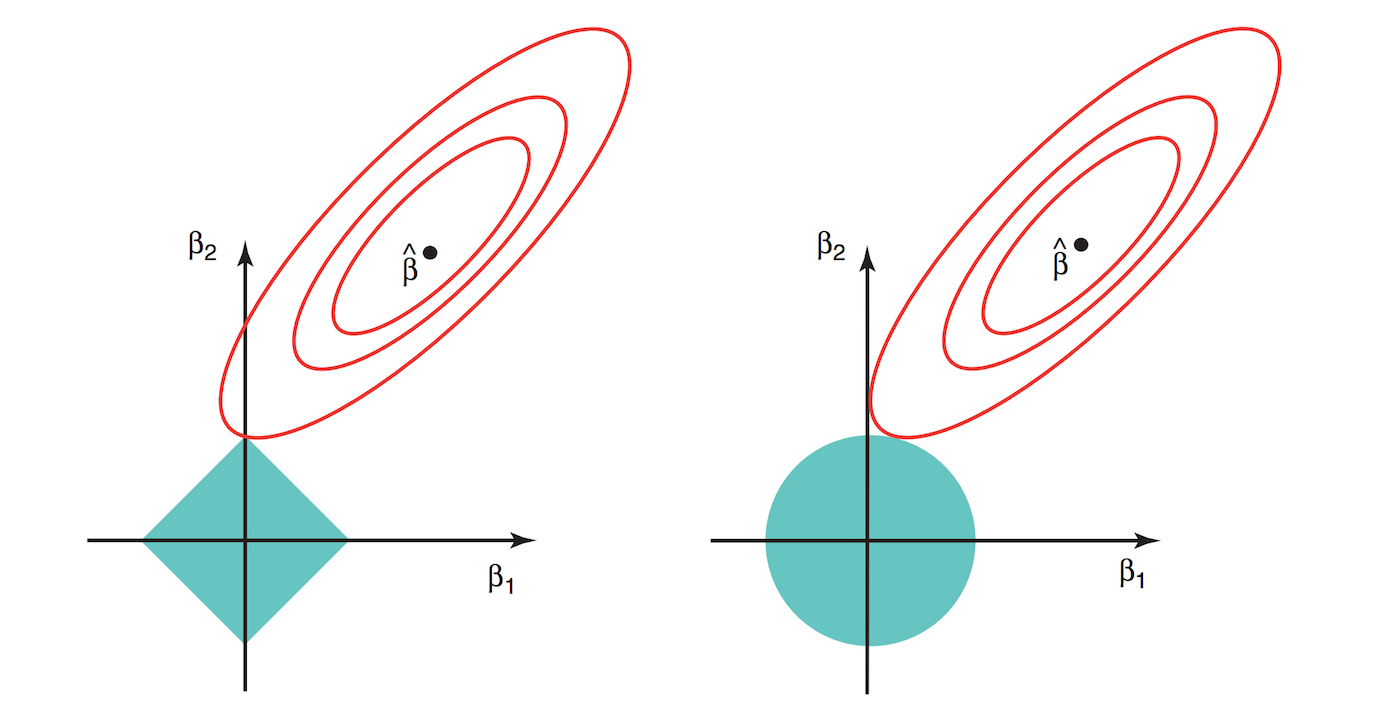
weight decay를 주게되면, Gradient descent algorithm이 loss space를 탐색할 때 제약조건을 받게되는 효과가 있음.(첫 번째 그림 청록색 영역)
-
제약조건 때문에, 특정 weight들이 사라지는 효과가 생기면서(0에 가까워짐) feature subset selection을 하는 효과가 있음.
