미분(Differentiation)
특정 검은색 점에서 어떻게 a,b에 대한 변화를 줘야 L이 줄어드는지 추정하여 파라미터 값을 변화시킴.
결국 알아야 할 건, 파라미터를 변화시킬 때 L값이 어떻게 변화하는지! ⇒ 미분
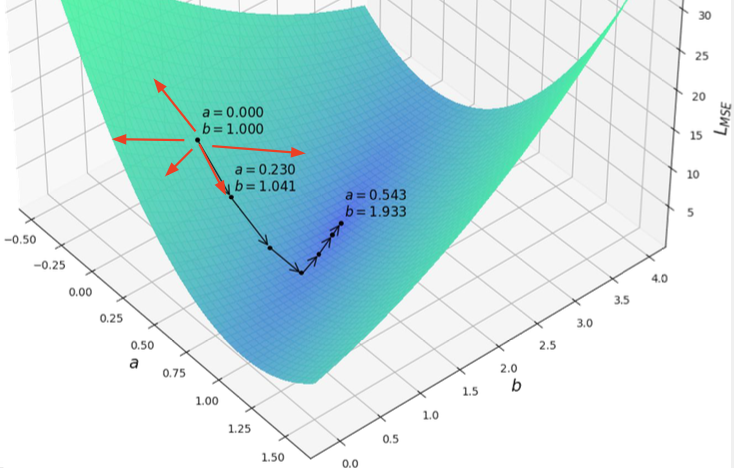
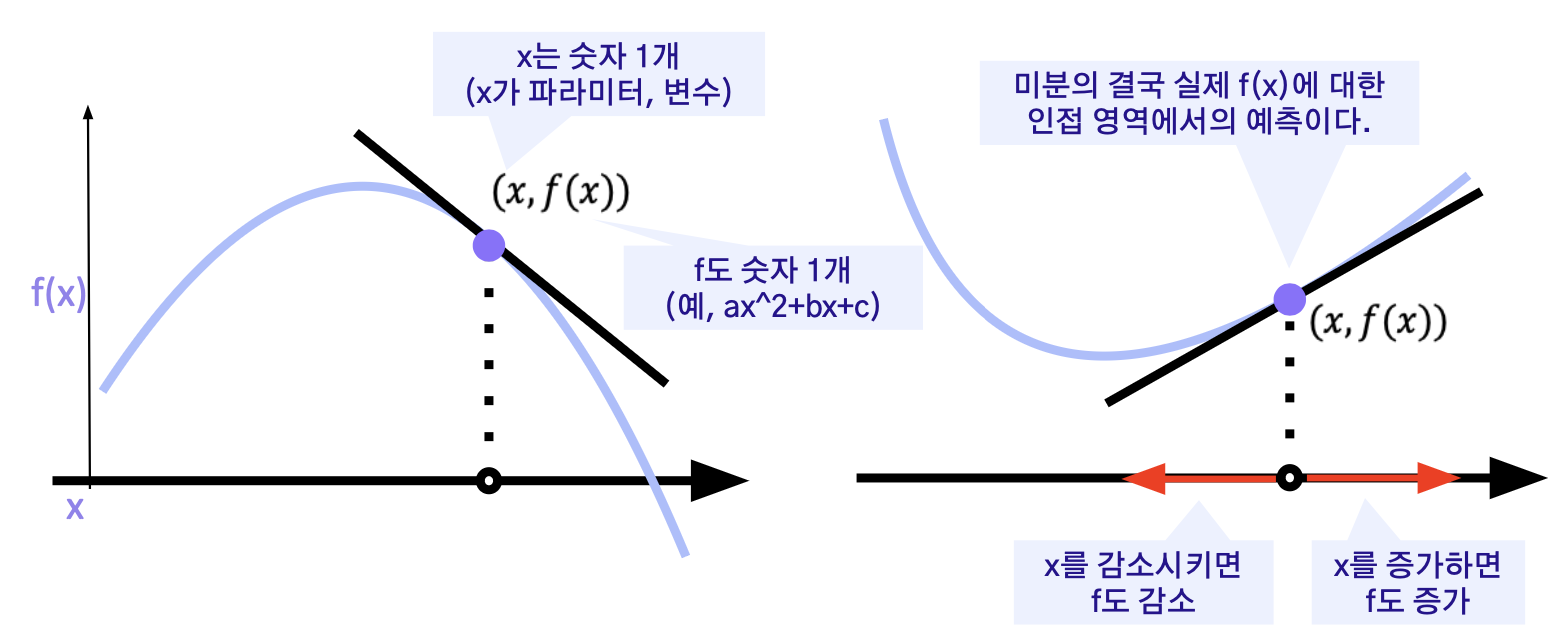
2차원 평면에서의 미분
미분값의 반대 방향으로 가면 감소!!
x → x – f '(x)
경사하강법
기울기가 감소하는 방향으로 x를 움직여서 f(x)의 최소값을 찾는 알고리즘.
딥러닝에선 손실 함수의 그래디언트가 감소하는 방향으로 파라미터를 움직여 손실 함수의 최소값을 찾는다.
한계 및 해결방안
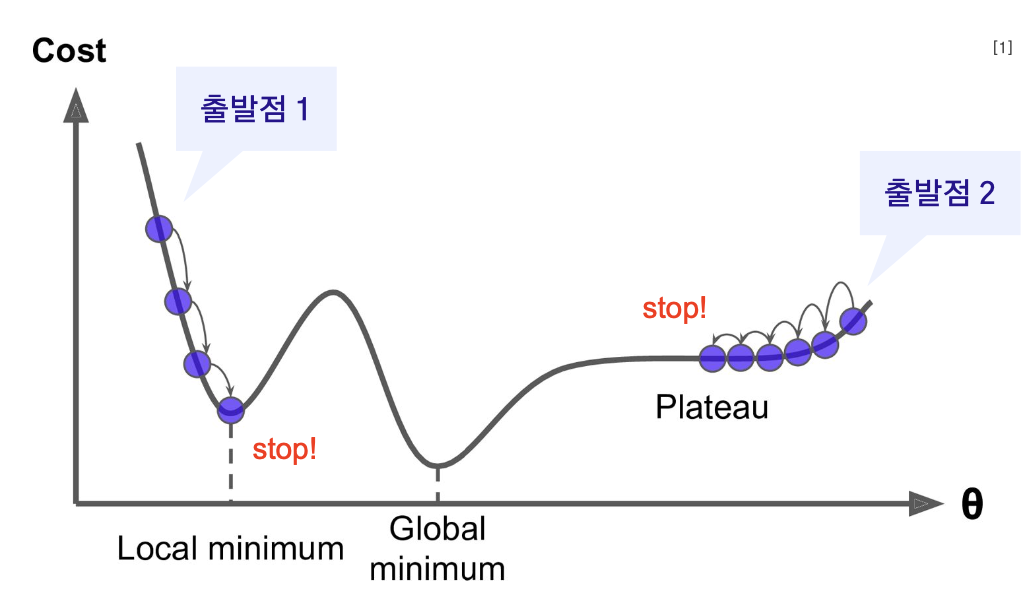
한계
-
로컬 미니멈(Local Minima): 경사 하강법은 로컬 미니멈에 갇힐 위험. 즉, 전역 최소값(Global Minimum)이 아닌 지역적 최소값에 도달하면 더 이상 개선되지 않을 수 있음.
-
학습률(Learning Rate) 설정: 적절한 학습률을 설정하는 것은 어렵. 학습률이 너무 높으면 수렴하지 않을 수 있고, 너무 낮으면 학습 속도가 느려짐.
-
고차원 및 비볼록성(High-Dimensionality and Non-Convexity): 고차원 데이터와 비볼록 손실 함수에서는 최적의 해를 찾기가 어려울 수 있음.
-
속도와 계산 효율: 대규모 데이터셋에서는 각 반복마다 모든 데이터를 사용하여 그래디언트를 계산해야 하므로 계산이 매우 느려질 수 있음. ==> 계산 효율을 위해 손실값을 샘플별 합이 아닌 평균값으로 : 확률적 경사하강법
해결방안
-
파라미터 초기화를 굉장히 잘한다.
(여러 초기화 기법, pretraining) -
모델 구조를 바꿔서 그래프 모양을 바꾼다.
-
Learning Step을 바꾼다.
확률적 경사하강법(SGD)
모든 데이터를 사용해서 구한 경사를 통해 파라미터를 한 번 업데이트 하는 대신, 데이터 한 개 또는 일부를 활용하여 구한 경사로 여러 번 업데이트를 진행
- SGD를 통해 한 번의 학습을 하는 데에 사용되는 데이터 샘플의 집합을 ‘미니 배치(mini-batch)’ 혹은 간단히 ‘배치(batch)’라고 부른다.
- 손실 함수의 크기를 1/m로 스케일하는 과정은 학습 데이터의 크기가 실시간으로 바뀌는 환경에서 특히나 잘 작동한다.
- m=1인 환경을 ‘온라인 학습(online/incremental learning)’이라고 부른다.
<확률적 경사하강법 파이프라인>
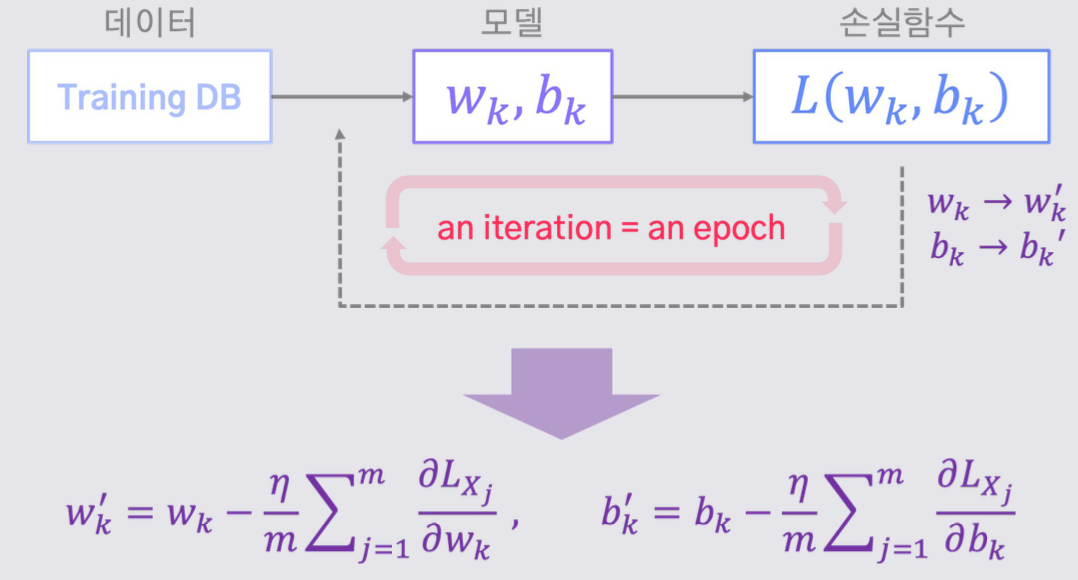
학습을 하기 위해서는 손실 함수의 그래디언트를 계산하는 과정이 불가피하다.
이것이 활성화 함수가 step function이 아닌 sigmoid function이 퍼셉트론에서 주로 사용되는 이유이다.
SGD vs GD
-
볼록하지 않은 목적식을 가진 경우, SGD가 GD보다 실증적으로 더 낫다고 검증되었다.
SGD는 학습에 활용하는 데이터 샘플이 매번 달라짐에 따라 손실 함수의 형태가 약간씩 바뀐다고 볼 수 있으며,(모델 구조를 간접적으로 바꾸는 효과)
이를 통해 local minima에 빠지는 것을 방지하여 최적해에 도달할 가능성을 높이는 방법으로 이해할 수 있다. -
데이터의 일부를 가지고 그래디언트 벡터를 계산하고 파라미터를 업데이트하므로 컴퓨터의 메모리 및 연산 자원을 좀 더 효율적으로 활용할 수 있다.
