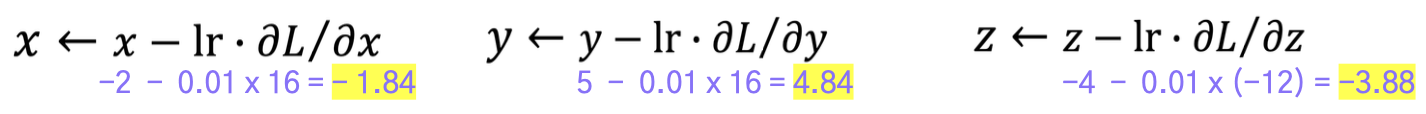손실함수의 기울기
모델의 각 파라미터에 대한 손실 함수의 기울기는 해당 파라미터가 잘못된 예측에 얼마나 기여했는지를 나타내게 되며, 경사 하강법을 적용하려면 모델을 구성하는 각 파라미터에 대해 손실함수를 미분한 결과(그래디언트)가 필요하다.
SGD로 손실함수 값의 미분 계산은 샘플 수를 줄여서 간단해졌지만, 모든 파라미터를 갱신 해야 하므로
모든 파라미터에 대한 미분 계산 필요 -> 복잡. 이를 위해 계산 그래프를 활용하여 모델 구조 표현
계산그래프
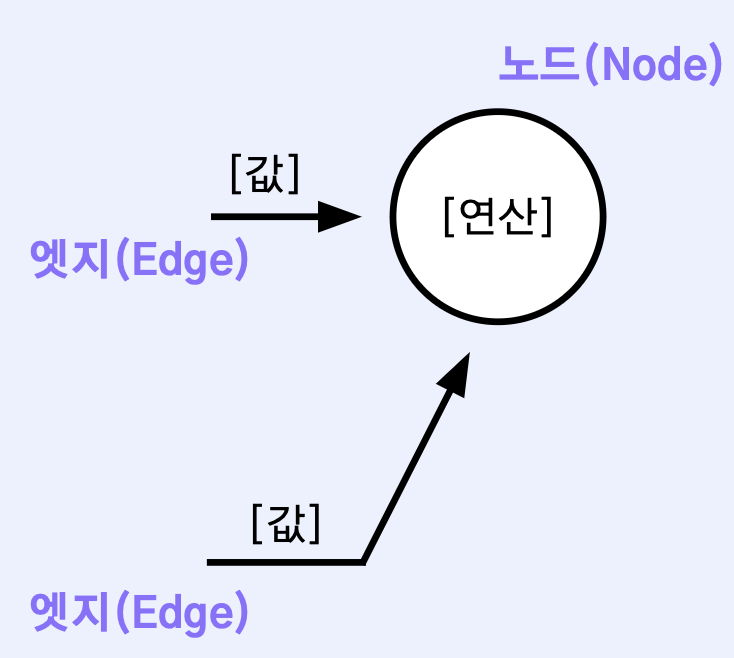
계산 그래프를 사용하면 편미분 계산이 가능하며, 중간 결과들을 보관하는 것이 가능
- 작은 문제에 집중하여 복잡한 문제를 단순화
- 각 변수에 대한 미분을 효율적으로 계산
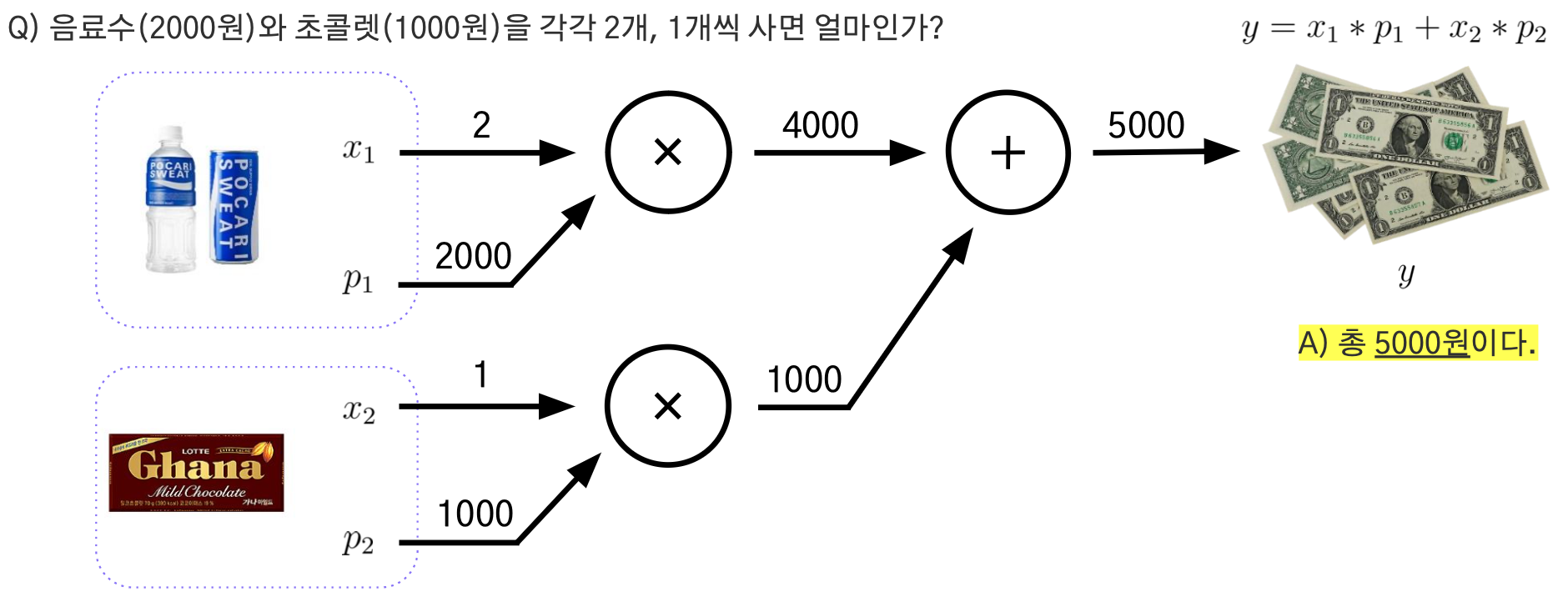
연쇄법칙(Chain Rule)
둘 이상의 연산이 수행된 합성 함수를 미분하기 위해, 연쇄 법칙(chain rule)을 사용한다.
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
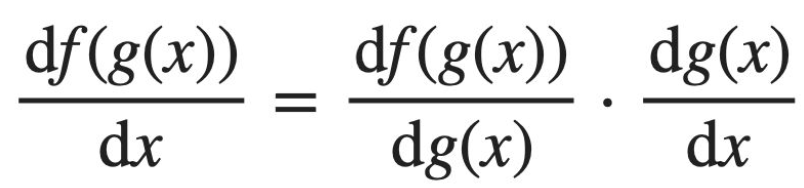
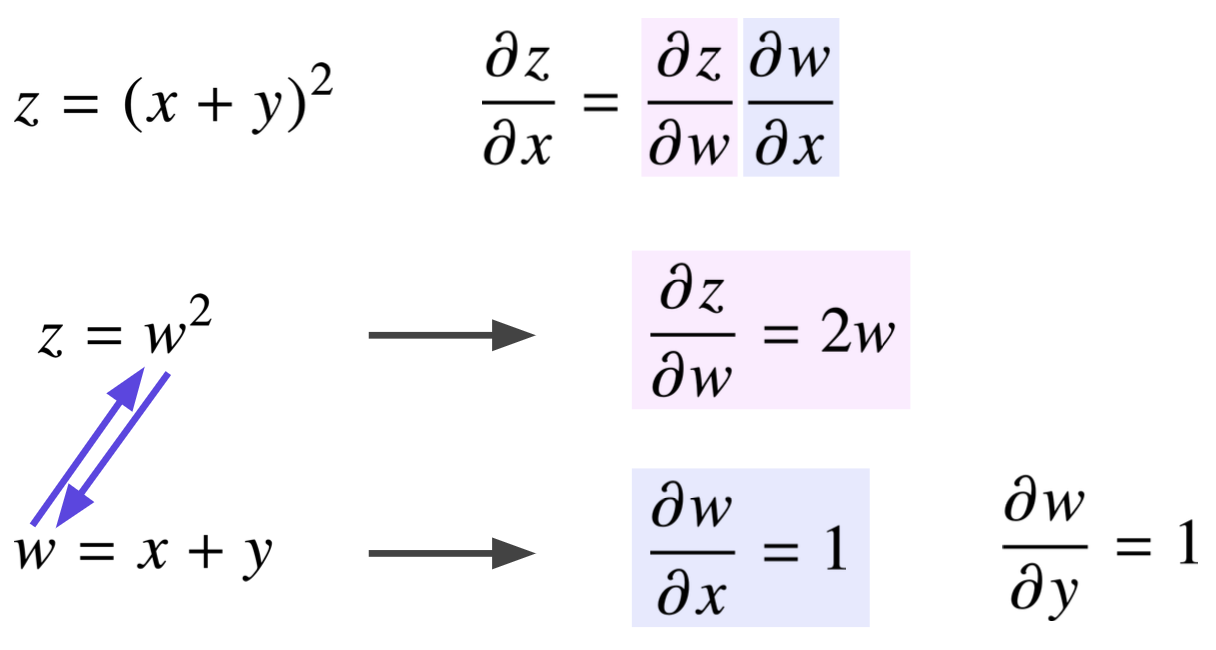
연쇄법칙과 뉴럴네트워크의 연관성
학습 중인 상황에는
- 파라미터가 (p1,p2,p3,p4) 특정 값을 가지고 있고,
- 학습 데이터의 특정 샘플에 (x) 대해서, 손실함수값을 계산할 수 있다.
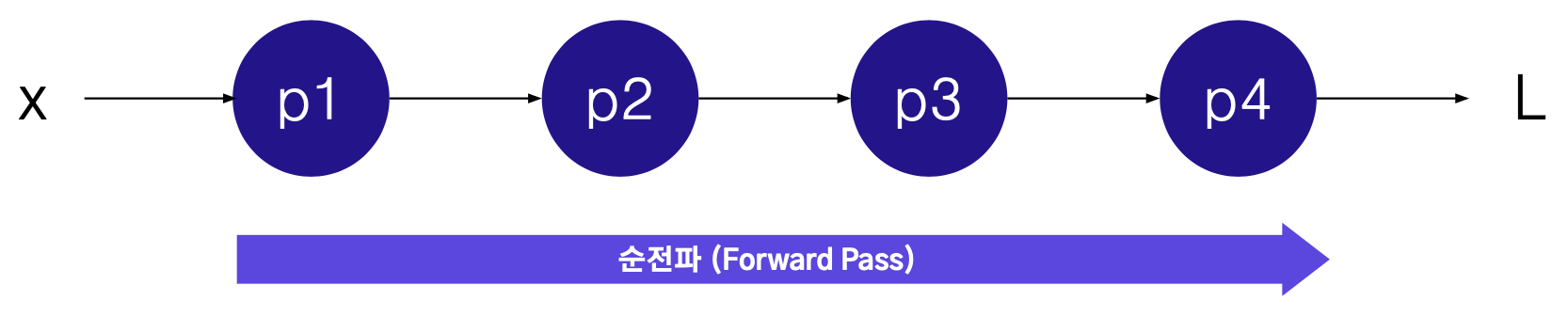
학습 중인 상황에서 파라미터를 업데이트 하기 위해서는
- 모든 파라미터에 대한 편미분을 (∂L/∂p1,∂L/∂p2,∂L/∂p3,∂L/∂p4) 구해야 하는데,
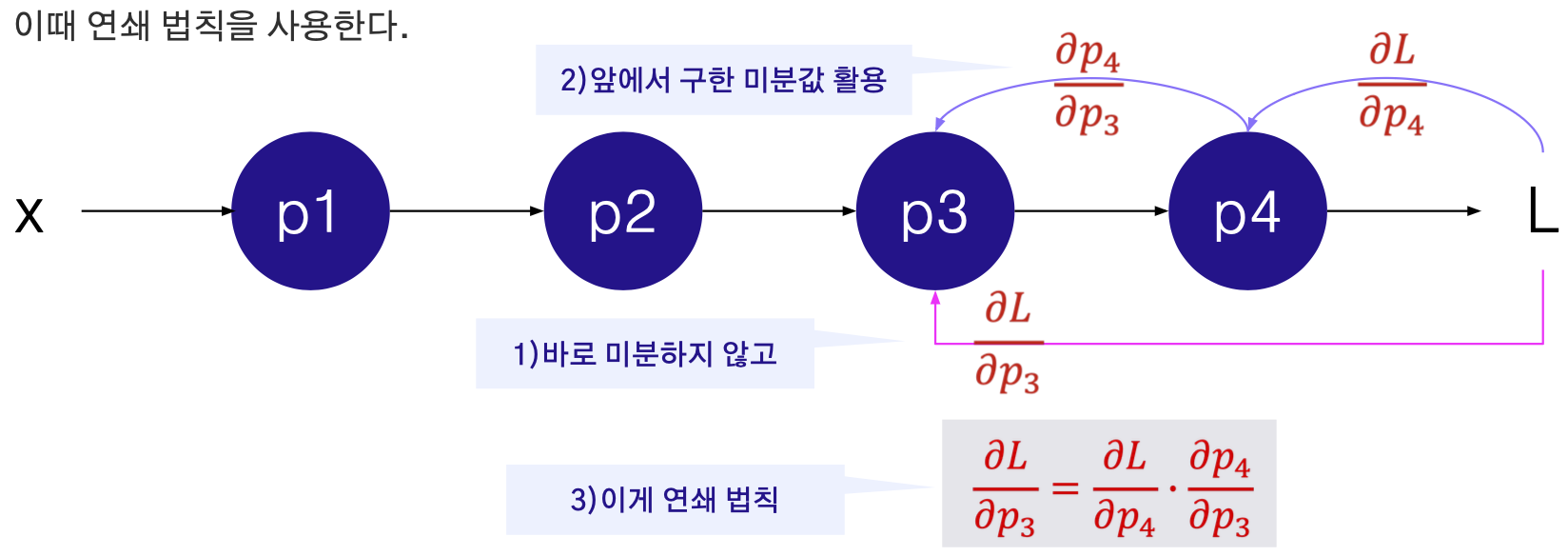
역전파 (Backpropagation): 각 노드에서의 편미분을 이전까지의 결과에 곱해서 뒤로 전달
역전파 알고리즘: 신경망의 추론 방향과 반대되는 방향으로 순차적으로 오차에 의한 편미분을 수행하여 각 레이어의 파라미터를 업데이트하는 과정
역전파의 이해
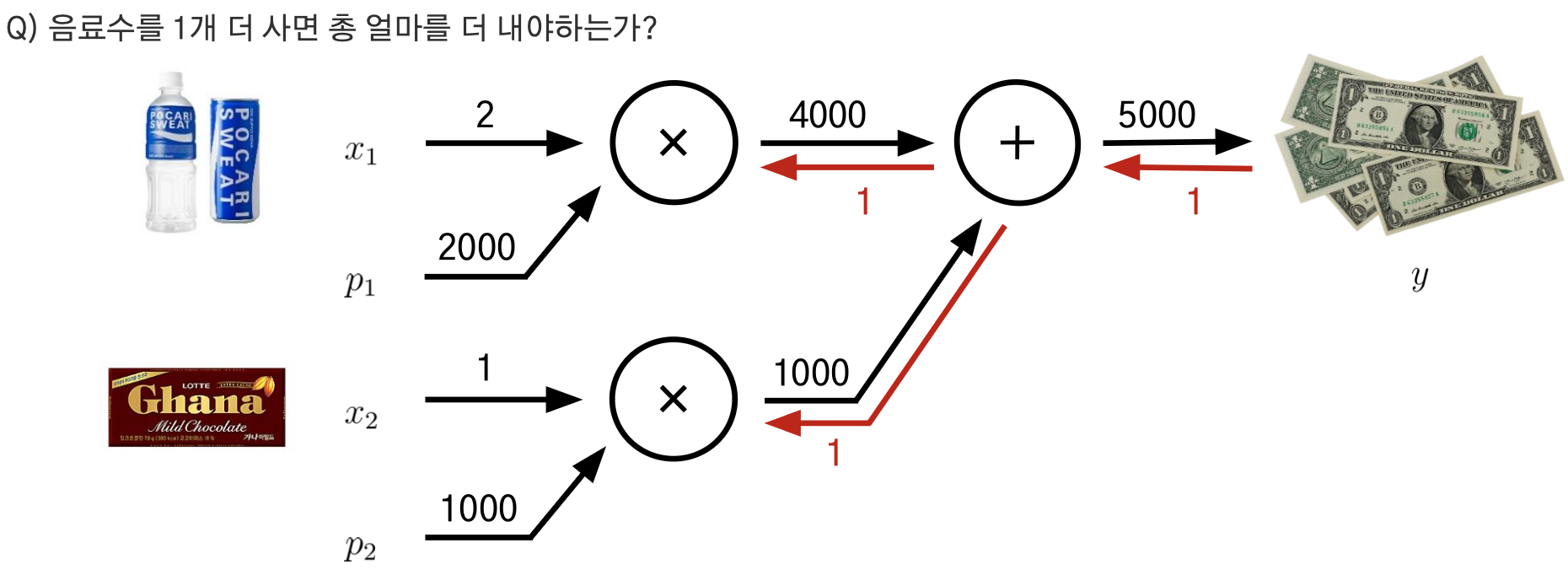
- 곱셈 노드 : 다른 엣지의 값을 곱해서 넘어간다
- 덧셈 노드 : 그대로 넘어간다
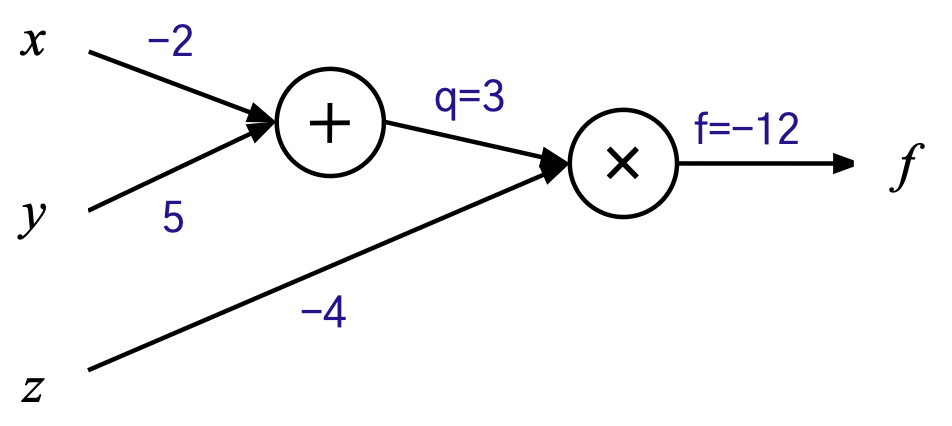
심화 예제 - 주어진 함수의 역전파 계산
- 함수 : f(x,y,z) = (x+y)z
- 데이터 : x= -2, y=5 , z=-4, target=-10
- 손실함수: L=(target - f)^2
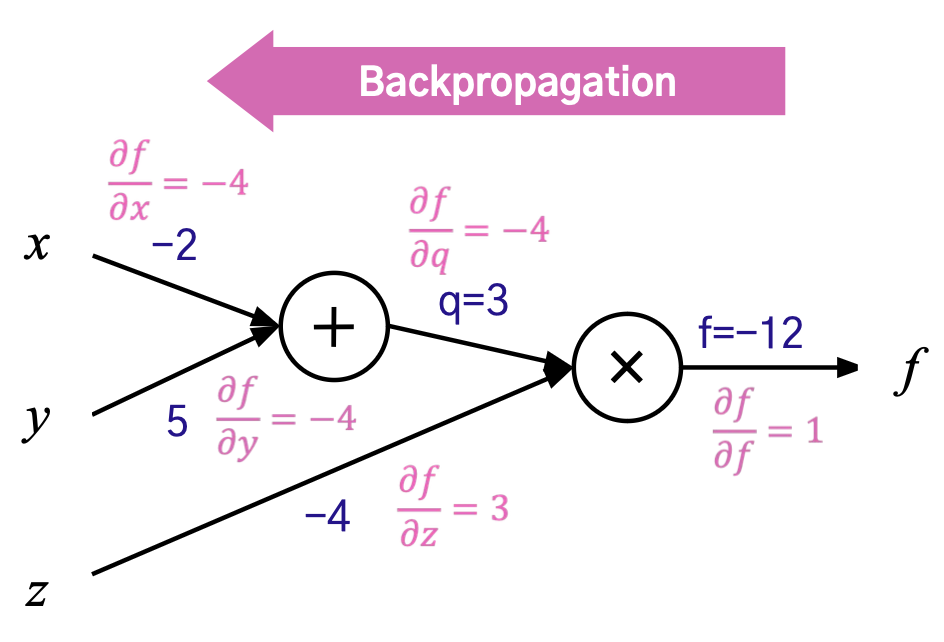
구해야하는 것: Loss에 대한 파라미터별 편미분
- → ∂L/∂f =∂L/∂f ⋅∂f/∂f
- → ∂L/∂x =∂L/∂f ⋅∂f/∂x
- → ∂L/∂y =∂L/∂f ⋅∂f/∂y
- → ∂L/∂z =∂L/∂f ⋅∂f/∂z
Parameter Update
손실함수에 대한 편미분은 앞서 구한 편미분 값에 ∂L/∂f 만큼만 곱하면 끝.
∂L/∂f = 2(f-target) =-4
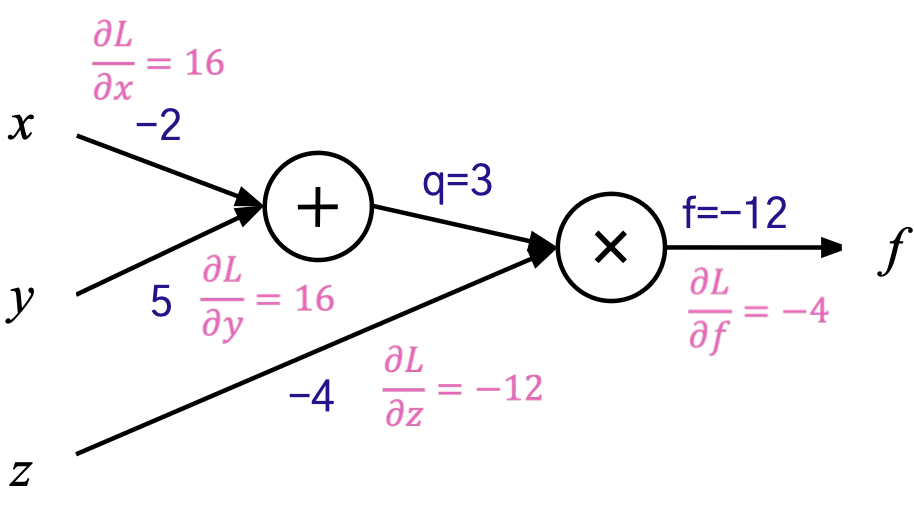
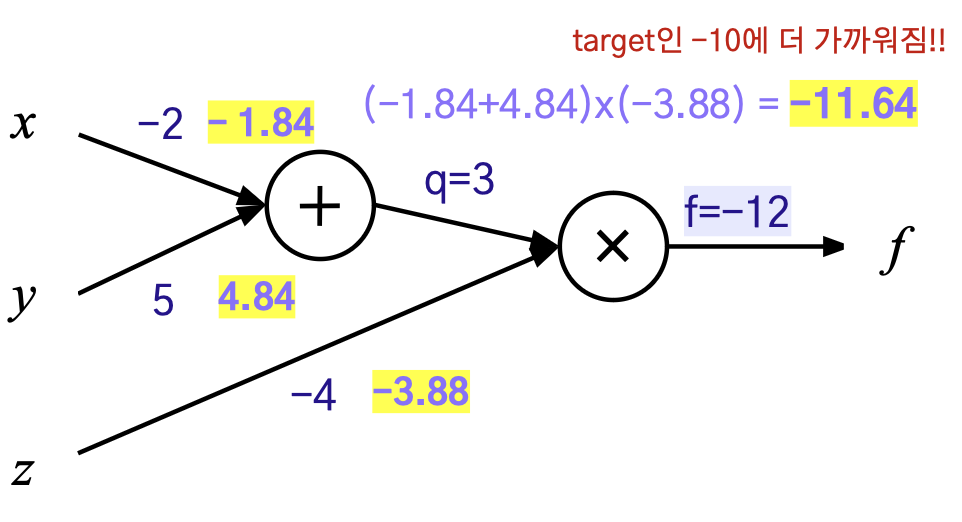
Parameter Update
현재 의 값은 -12로, 타겟으로 하는 -10과 다르다.
→ 각 파라미터에 대해 편미분한 값에 학습률을 곱한 값만큼
원래의 파라미터에 빼서(반대방향: 기울기가 감소하는 방향) 모델을 업데이트한다. ex) learning rate = 0.01