손실함수의 기본가정
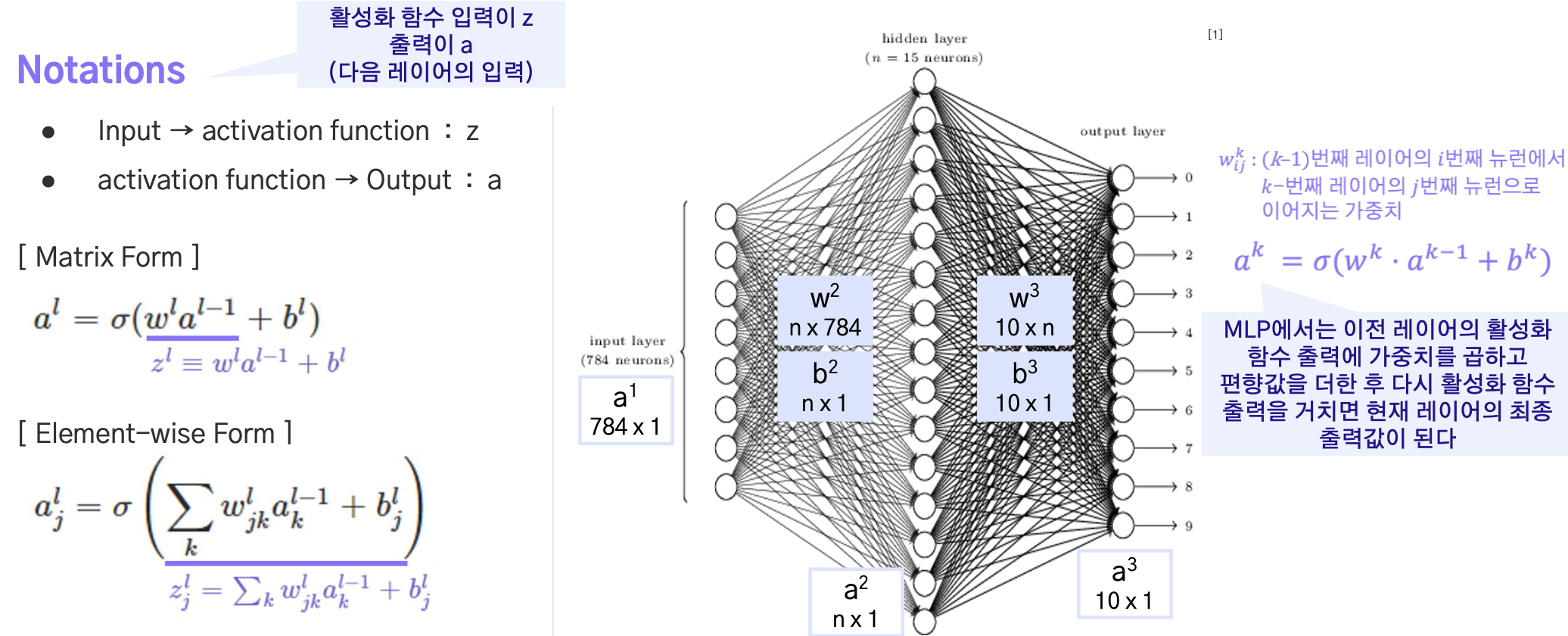
활성화함수는 sigma로 표현, input,output , matrix form의 이해 중요
역전파가 충족시켜야하는 손실함수의 조건
손실(=비용)함수에 대한 가정 1
학습 데이터 샘플에 대한 신경망의 .총 손실은, 각 데이터 샘플에 대한 손실의 합과 같다
-> 이게 아래 사진 첫 번째 표현(합의 형태), 두 번째 표현(모든 샘플별 손실값에 대한 곱 = 최종손실) 처럼 표현하면 역전파 기법 사용 불가: 비용함수는 설계하기 나름
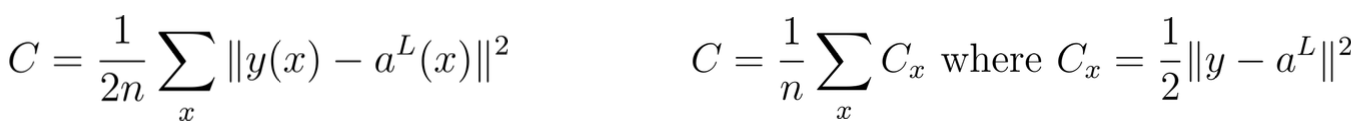
이 가정을 통해, 아래와 같이 손실 함수의 편미분을 계산할 수 있다.

합쳐서 편미분한거랑 편미분해서 합친거랑 같음.
따라서 우리는 전체 손실(∂C/∂w)이 아닌 각 데이터에 대한 손실(∂Cx/∂w)에만 집중할 수 있다.
손실(=비용)함수에 대한 가정 2
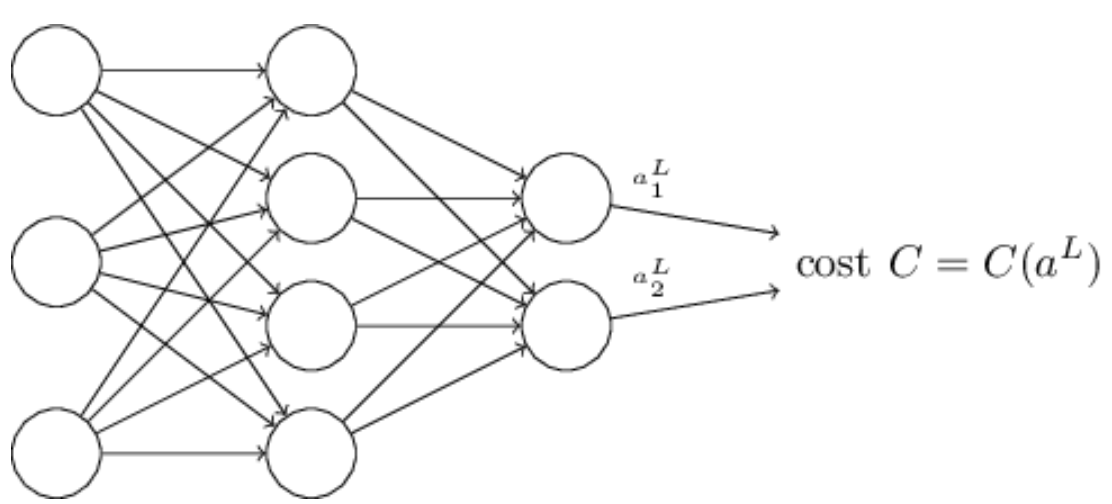
각 학습 데이터 샘플에 대한 손실은 aL에 대한 함수이다.
= 모델의 최종 출력에 대한 함수로만 정의를 해야 역전파 기법 사용가능
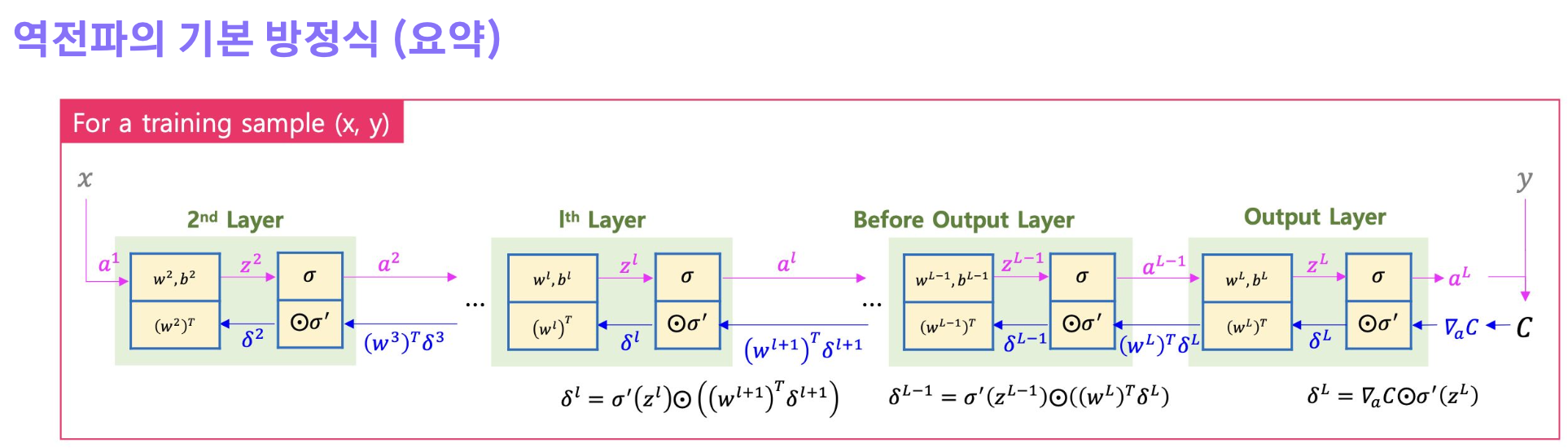
역전파의 기본 방정식
Notations
에러는 특정 레이어의 특정 뉴런에서의 z값을 (활성화 함수 입력값) 조금 변화 시킬 때, 비용 함수값이 얼마나 변화되는지에 대한 편미분
기본 방정식