손실함수

손실함수의 중요성

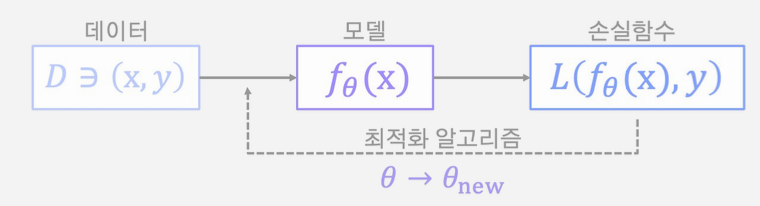
손실함수가 작아지도록 파라미터를 조정했기에, 어떤 손실함수를 사용하느냐에 따라 학습 결과가 다르다

대표적인 손실함수

평균제곱오차(MSE)

실제값(y)과 모델의 추정한 값(y) 사이의 차이를 제곱하여 평균낸 값 또는 함수

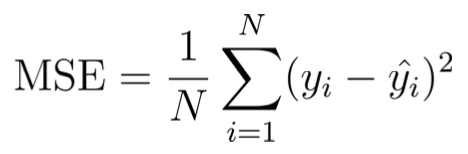
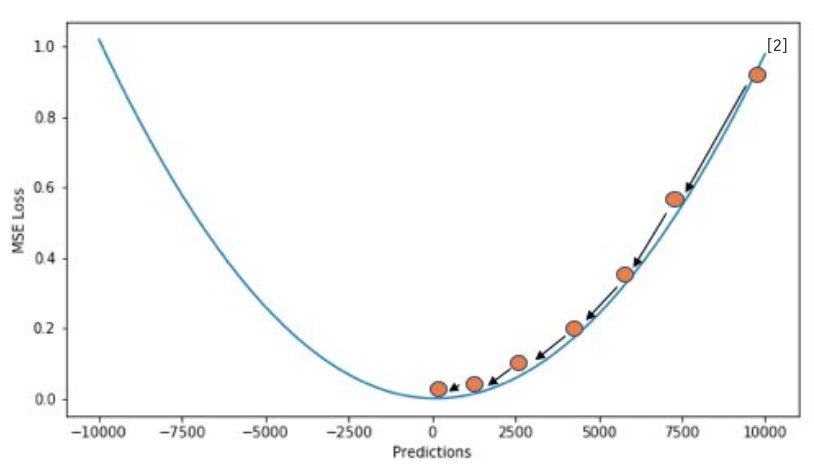
• Quadratic Loss 또는 L2 Loss 라고도 불린다.
• 실제값과 추론값 사이의 오차가 제곱항으로 더해지므로 초반 학습이 빠르나(최소값에서 멀수록 미분값이 크므로) 이상치(outlier)에 민감(큰 값은 더욱 크게 되므로)하다는 특징을 가진다.

평균절대오차(MAE)

MSE가 이상치에 민감하다는 단점을 보완 그럼 절대치로 하면 되지않냐

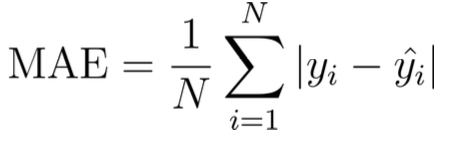
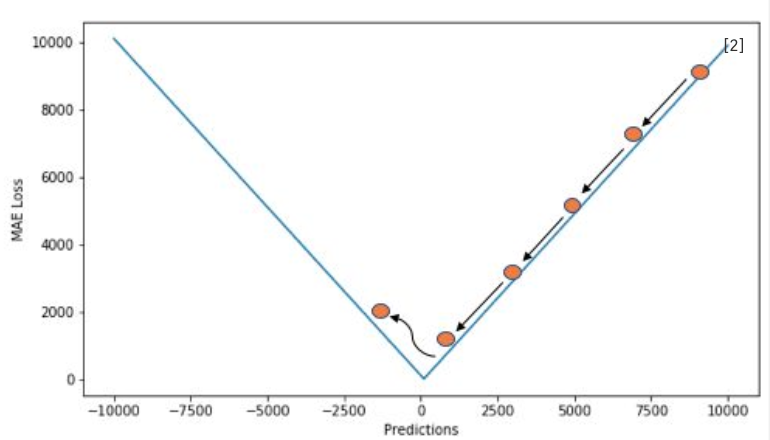
• L1 Loss 라고도 불린다.
• 추정하고자 하는 값과의 단위가 같기 때문에 직관적으로 이해하기 쉽다.
• 손실 함수의 값이 최소값에 가까워져도 미분값은 동일하기 때문에
  점핑이 일어날 수 있으며 손실 함수의 크기를 직접 줄여주어야 한다.

Huber Loss

오차가 일정 수준 이하일 때는 MSE, 그렇지 않을 때는 MAE를 사용하여 두 손실 함수의 장점을 결합한 방법

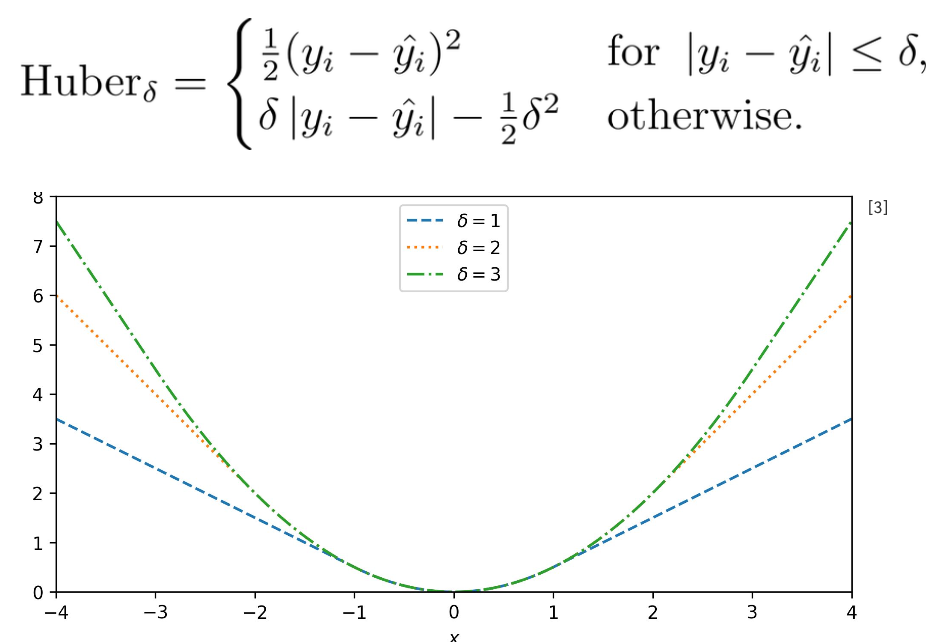
Cross Entropy(CE)

주어진 확률 변수 또는 사건 집합에 대한 두 확률 분포 간의 차이를 측정하는 함수
P는 정답 분포, q는 예측 분포

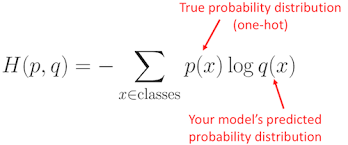
손실함수의 해석

Backpropagation 관점

Vanishing Gradient Problem

레이어의 수가 증가할수록 활성화 함수의 미분값(0~1)이 계속해서 곱해져, 가중치에 따른 미분값이 0에 수렴하게 되는 문제

Loss Type 1: MSE

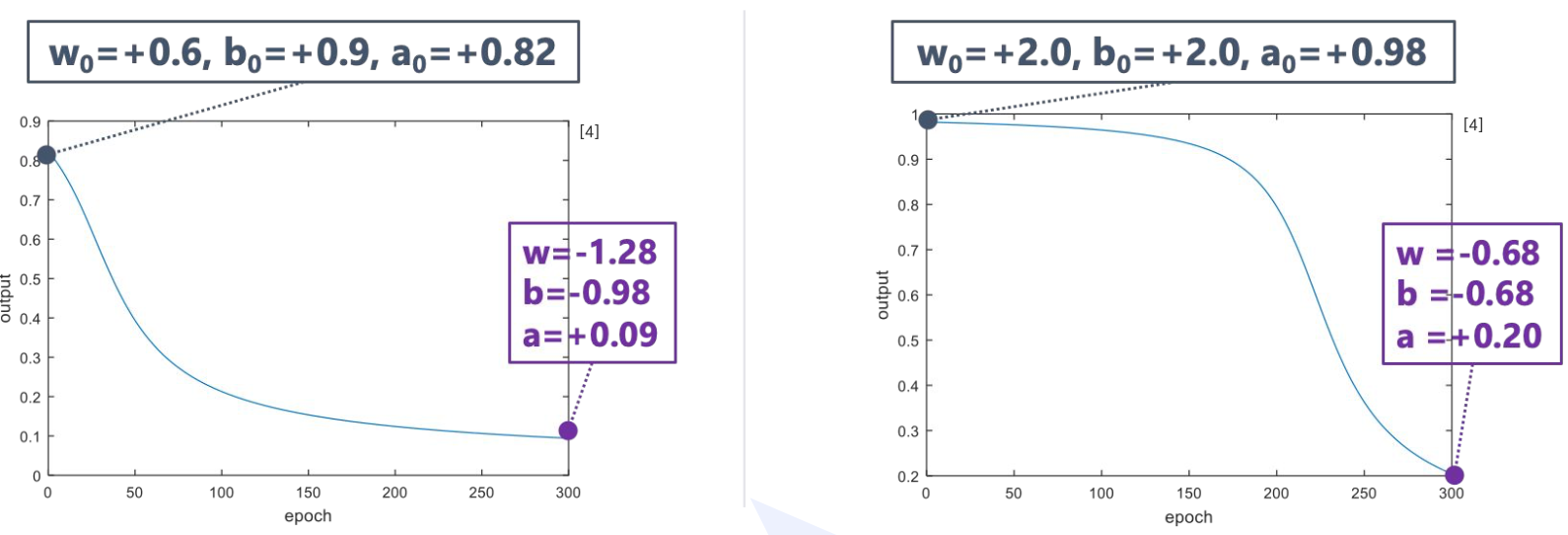
파라미터를 서로 다른 값으로 초기화 한 후 동일 epoch 수가 지난 후 멈췄더니 학습 경향이 많이 다름

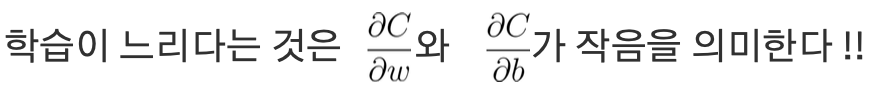
Q. 왜 미분값이 작게 나올까?
-> A) 활성화 함수인 시그모이드 함수가 곱해지기 때문

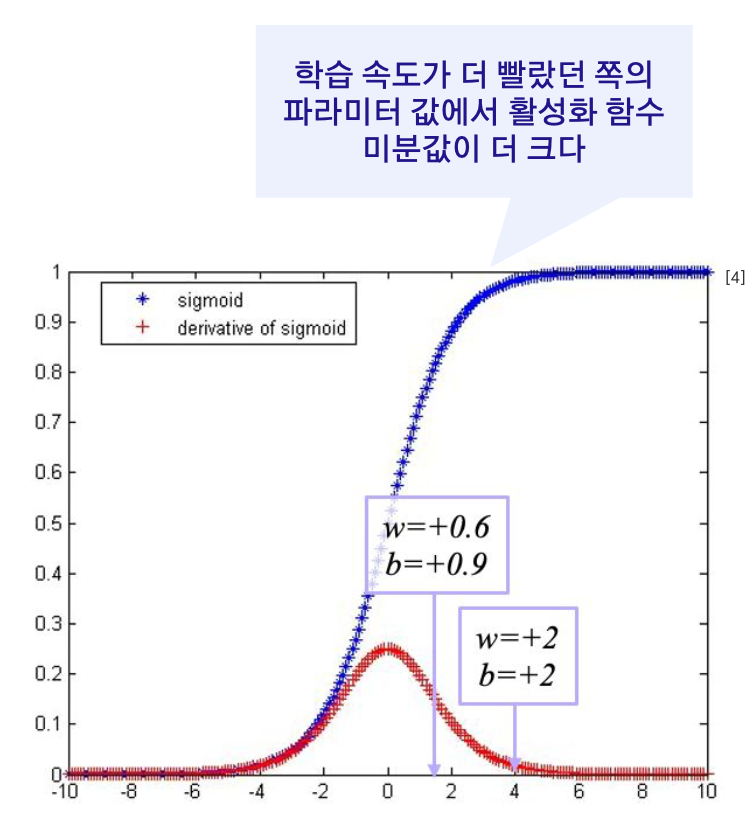
Loss Type 1: CE

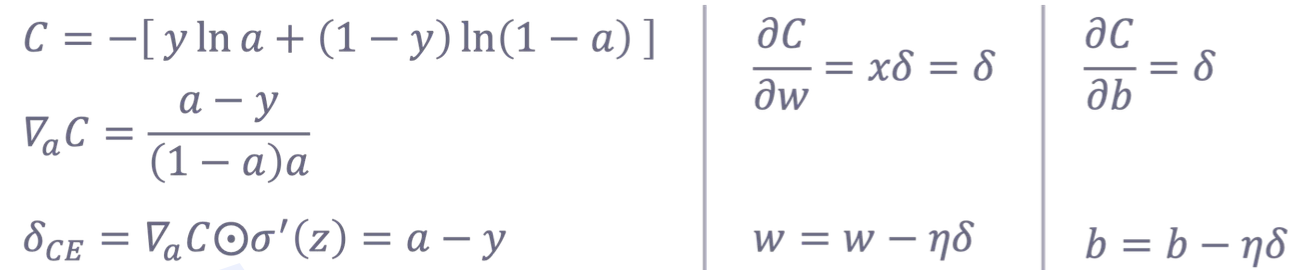
MSE VS CE

• MSE와는 달리 CE는 출력 레이어에서의 에러값에 활성화 함수의 미분값이 곱해지지 않아 gradient vanishing problem에서 좀 더 자유롭다. (학습이 좀 더 빨리 된다)
• 그러나 히든 레이어의 노드들에서는 활성화 함수의 미분값이 계속해서 곱해지므로
  레이어가 여럿 사용될 경우에는 결국 gradient vanishing problem에서 완전 자유로울 수 없다.
• 이러한 관점에서, 활성화 함수의 미분값이 0 또는 1로만 표현되는 ReLU는 훌륭한 선택이지다.

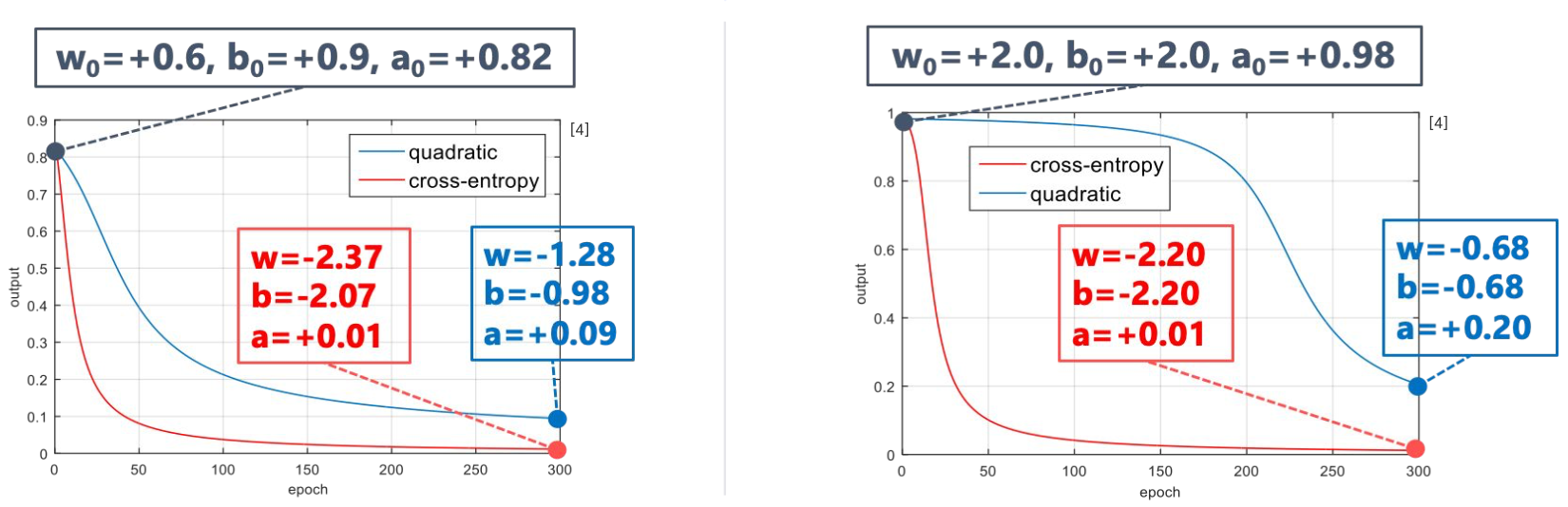
동일 파라미터 값에서 손실 함수를 다르게 쓸 때의 차이점

Maximum Likelihood 관점