Perceptron
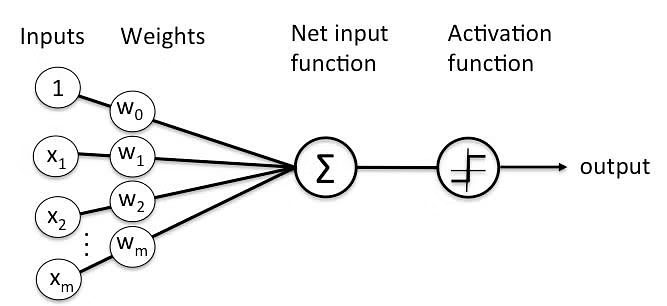
실제 뉴런이 신호를 받아 처리하고 출력하는 과정을 수학적으로 표현한 것
이전 레이어의 모든 뉴런들과 현재 레이어의 어떤 특정 뉴런들이 연결되어 있는데 넘어오는 신호를 개별의 가중치를 둬서 합침. 이때 임계치보다 크면 1(다음으로 넘김) 아니면 0(안넘김) 출력
퍼셉트론 예시: 이진수 입력, 이진수 출력
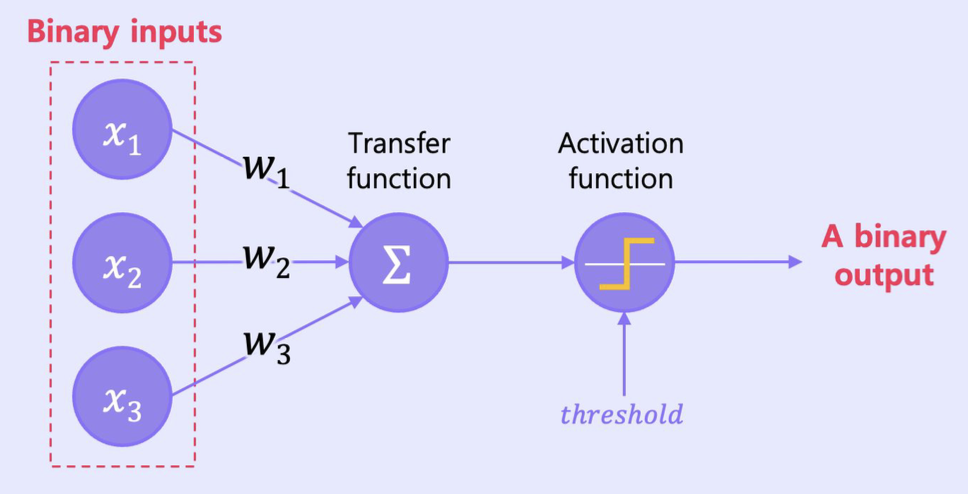
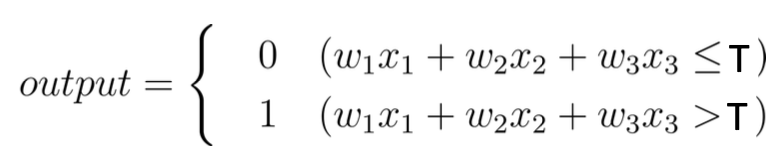
퍼셉트론 예제
x1 = 1 : 연말까지의 매출이 100억이 넘는다.
x2 = 1 : 전사 인원이 100명이 넘는다.
x3 = 1 : 희망 참석률이 80%를 넘는다.
output = 0 : 방~~~콕
output = 1 : 연말에 전사 시드니 해외 워크샵을 간다!
가중치와 임계치를 변화시키며 다양한 의사 결정 모델을 만들 수 있다!
z = (w1x1+ w2x2+ ... + wnxn)+ w0
=> 즉, w0(bias)가 클수록 출력값이 쉽게 1이 된다!
이러한 퍼셉트론은 입력에 대한 선형 분리의 특징을 가짐
-> 일반화하면 선형식을 통한 분리로 이해 가능하기 때문
그럼 퍼셉트론들을 여러가지를 다양하게 엮으면 어떠한 연산들이던지 표현가능하겠네?
-> 다층 퍼셉트론
Multi-Layer Perceptron
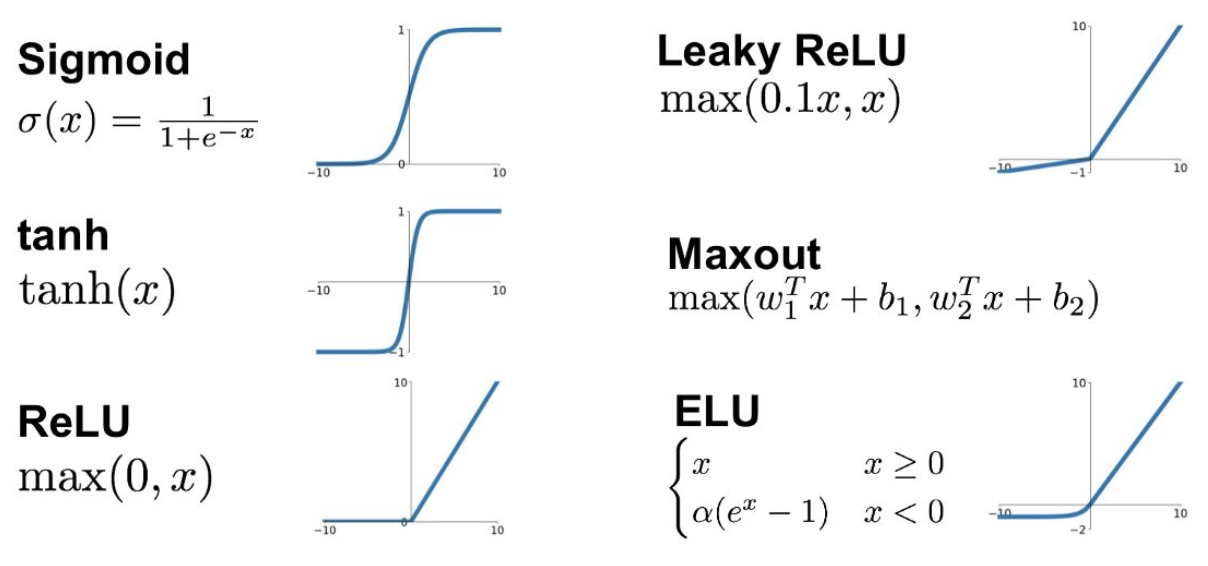
활성화 함수
입력 신호의 총합을 출력신호로 변환하는 함수 -> 근데 z만 있으면 되는 거 아님? 왜 필요?
사용이유
여러 개의 퍼셉트론을 사용하지만 결과적으로 여러 개의 계산이 선형분리냐 비선형 분리냐에 따라서 필요여부 결정
- 활성화함수가 없으면 단순 선형식으로 표현 가능하므로 굳이 다층퍼셉트론을 쓸 이유가 사라짐
(z의 일반적인 표현은 w⋅x+b = Wx 형태로 표현 가능
x = [x,1], W = [w,b]’) - 선형식보다 비선형식이 구분하는게 성능이 더 좋을 때가 많음!

종류
현실에서는 Step Function이 아닌 다른 종류의 활성화 함수들이 사용되고 있음.
- 현실에서는 단순히 임계치로 이진화 출력을 내는 것이 아니기 때문.
Sigmoid Function
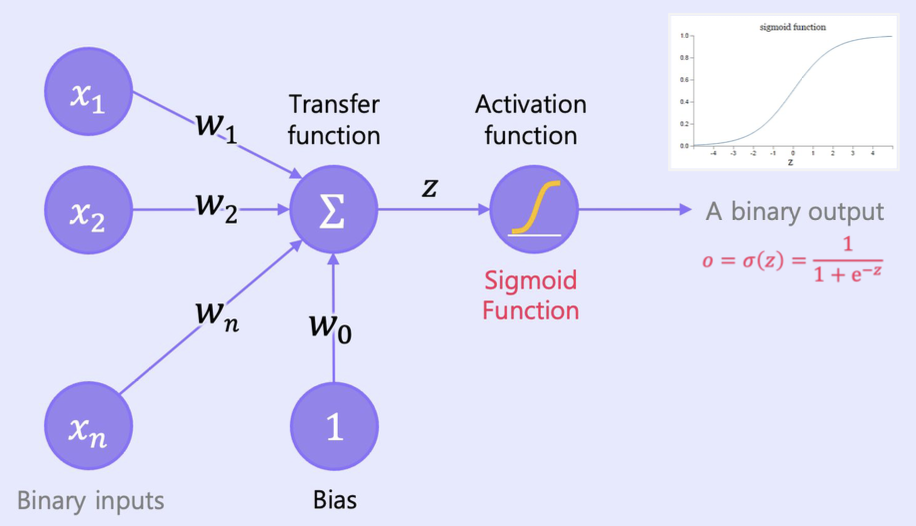
step function과는 다르게,
연산 과정 전체를 미분 가능하게 만드는게 큰 목적 => 역전파 기법과 연관
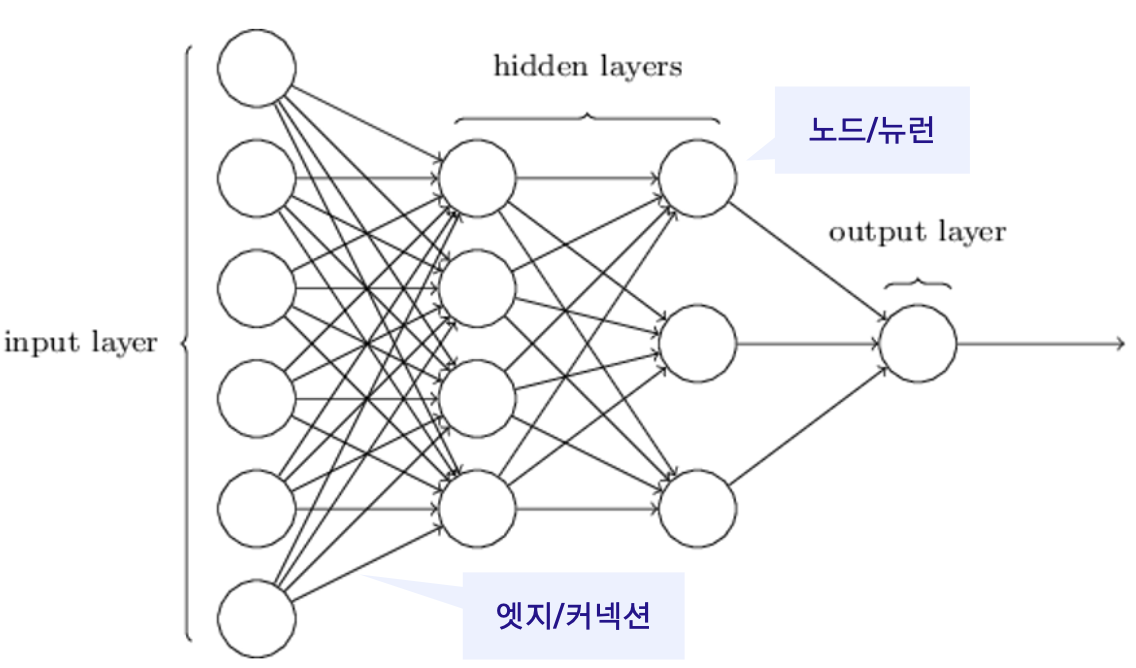
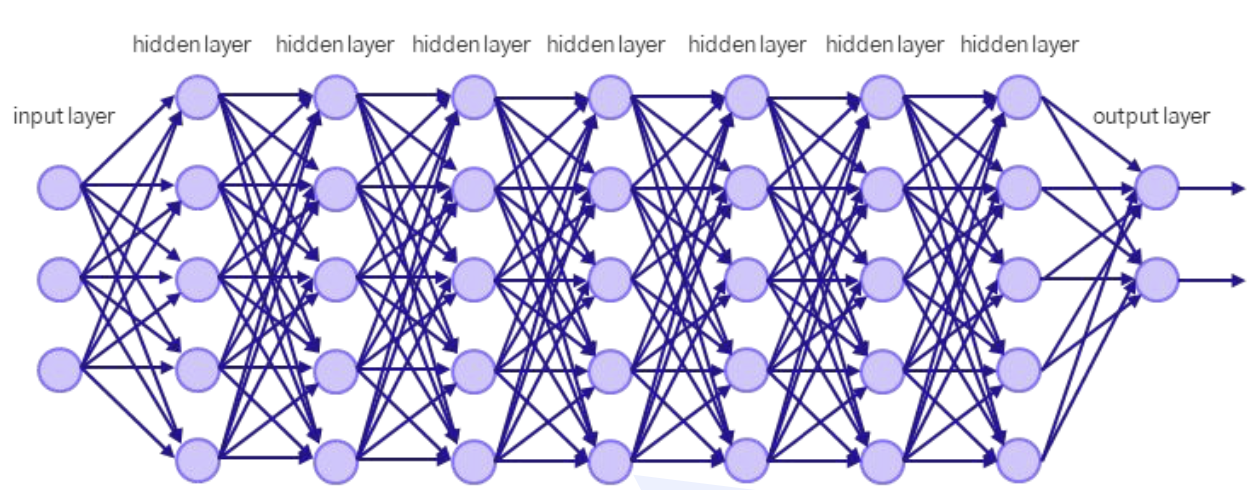
MLP 구조
노드(node)/뉴런(neuron)
: Transition (z) + Activation Function
● 레이어/층(layer)
- 입력층(input layer)
- 은닉층(hidden layer)
- 출력층(output layer)
● 엣지(edge), 커넥션(connection) : 가중치(weight)를 의미
레이어 수가 4인 MLP 예시