선형 회귀

선형 회귀(Linear Regression)

• 지도 학습 - 회귀 분석에 속한다.
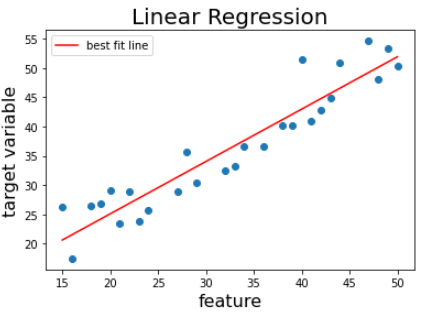
• 데이터들을 가장 잘 대표하는 선(최적선, line of best fit)을 찾는다.
• 새로운 데이터들을 최적선을 통해 예측한다.
• 목표 변수(target variable): 맞추려고 하는 값
• 입력 변수(feature): 맞추는데 사용하는 값

장단점

• 장점: KNN의 경우 데이터 범위가 예측 가능 범위이지만, 선형 회귀의 경우 범위 제한이 없다.
• 단점: 이상점(Outlier)에 취약하다.

가설 함수(hypothesis function)

　　　　　　　　　　　$h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + ...$

• 최적선을 찾기 위해 시도하는 함수
• 선형 회귀로 찾으려는 것이 최적의 $\theta$ 값들이다.

가설 함수 표기가 h(x)가 아니라 $h_\theta(x)$인 이유 ($h(x)$라고 써도 된다.):
가설 함수에서 $x$는 변하지 않기 때문에 $\theta$가 매개변수로 작동하기 때문이다.

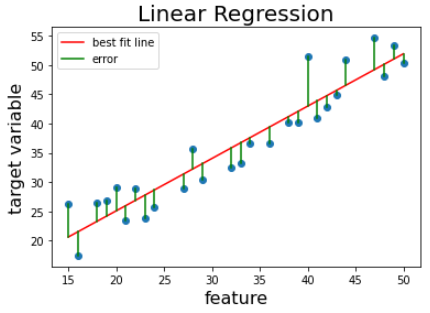
평균 제곱 오차(MSE)

　　$MSE = \displaystyle\frac{1}{m}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2}$ (훈련 데이터 m개, $x^{(i)}, y^{(i)}$는 각각 i번째 데이터의 인풋, 아웃풋)

• 예측값과 실제 값의 차이의 제곱의 평균
• MSE가 작다 -> 가설함수가 데이터에 잘 맞다.
• MSE가 크다 -> 가설함수가 데이터에 잘 안 맞다.

제곱을 하는 이유:

• 오차가 음수인 경우 고려
  • 음수인 경우를 고려해 절댓값을 사용해도 되지만 그럴 경우 미분이 불가능한 지점이 생긴다.
• 오차가 커질수록 부각시키기 위해서

손실 함수(Loss Function)

• 가설 함수의 성능을 평가하는 함수
• $J(\theta)$로 표현한다.
• 손실함수가 작다 -> 가설 함수가 데이터에 잘 맞다.
• 손실함수가 크다 -> 가설 함수가 데이터에 잘 안 맞다.
• 머신 러닝 알고리즘에 따라 달라질 수 있다.

비용 함수(Cost Function)라고도 부른다.

선형 회귀에서는 아래와 같이 MSE를 사용한다. (2m이 된건 계산 편의를 위한것)
$J(\theta) = \displaystyle\frac{1}{2m}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2}$

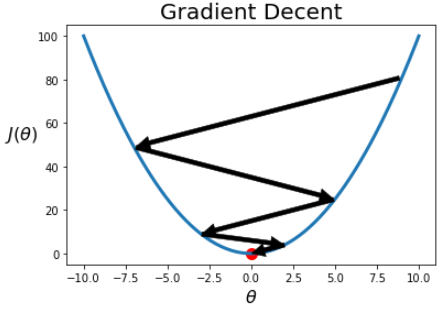
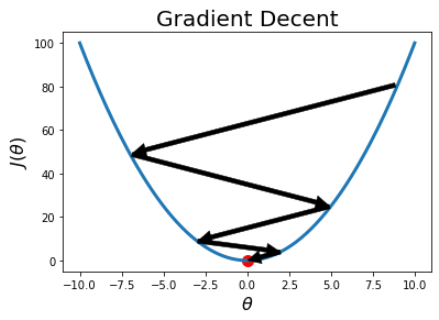
경사 하강법(Gradient Decent)

• 손실 함수의 값을 최소화하는 방법 중 하나
• 손실을 가장 빠르게 줄이는 방향으로 $\theta$값을 수정한다.
• $\nabla J(\theta)$를 구한 뒤 다음과 같이 $\theta_i$를 업데이트한다.

　　　　　　　　　　　　　　　　　　　　$\theta_i$ <- $\theta_i - \alpha\dfrac{\partial}{\partial \theta_i}J(\theta)$

• 위의 과정을 반복하면 손실함수의 극소점에 해당하는 $\theta$를 찾을 수 있다.

경사 하강법의 장단점

• 장점: 차원에 대한 제약이 없다. 즉, 모든 차원에 대해서 적용이 가능하다.(특성 수에 민감하지 않다.)
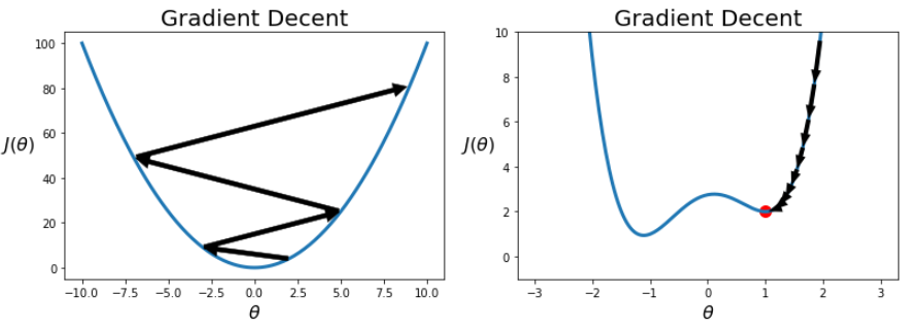
• 단점: 정확성을 위해 극값으로 이동하는데 많은 과정을 거쳐야 하며, 시작 위치와 주어진 함수에 따라 극값이 아니라 발산할 수도 있고, 극값이 최솟값이 아닐 수도 있다.

학습률(Learning Rate or Step Size) alpha

• 학습률은 $\theta$의 변화량을 조절하는 값이다.
• 학습률이 너무 크면 Overshooting, 즉, 극점으로 수렴이 아니라 발산될 수 있다.
• 학습률이 너무 작으면 극점에 도달하는데 너무 많은 반복을 거치거나, global minimum이 아닌 local minimum에 도달할 수 있다.
• 적절한 alpha: 손실이 잘 줄어들면서 iteration이 적은 alpha
• 따라서 적절한 alpha를 찾기 위해 (0.01, 0.1, 1, 10, 100 등 10의 제곱으로) alpha 여러개를 테스트 해보면서 적절한 alpha를 찾는다.

경사 하강법의 종류

배치 경사 하강법(Batch)

• 매 경사 하강법 스텝에서 전체 훈련 세트 $X$에 대해서 계산한다.(매 스텝에서 훈련 데이터 전체를 사용한다.)
• 정확도가 높은 대신(전역 최솟값에 도달할 확률이 높다.) 매 스텝에서 훈련 데이터 전체를 사용하므로 다른 경사 하강법에 비해 학습속도가 느리다.

확률적 경사 하강법(SGD, Stochastic Gradient Descent)

• 매 스텝에서 한 개의 샘플을 무작위로 선택하여 그 샘플에 대한 gradient를 계산한다.
• 매 스텝에서 하나의 샘플에 대해서만 계산하므로 데이터 양이 많아도 속도가 빠르다.
• 손실함수가 불안정할 때, 지역 최솟값을 빨리 탈출할 수 있지만, 반대로 전역 최솟값에 도달하지 못할 수 있다.(이는 학습률을 점진적으로 감소시켜 해결한다.)
• 학습률의 감소율에 따라 학습 결과가 달라지므로 적절한 감소율을 설정해야 한다.

미니 배치 경사 하강법(Mini-Batch)

• 매 스텝에서 미니배치라고 부르는 임의의 작은 샘플 세트에 대해서 gradient를 계산하는 경사 하강법이다.
• 배치 경사 하강법과 SGD의 중간 정도의 장단점을 가지고 있다.
• 행렬 연산에 최적화된 H/W 특히, GPU를 사용해 성능향상을 얻을 수 있다.

평균 제곱근 오차(RMSE)

• 모델이 예측을 얼마나 잘하는지 평가할 때 사용한다.
• $\sqrt{MSE}$
• 원래 데이터의 단위가 MSE를 구하면서 제곱이 되어 의미를 파악하기 어렵기 때문에 제곱근을 사용하여 원래대도 되돌리기 위해 사용한다.

제곱근이 적용되어 RMSE는 작을 수밖에 없다.
-> 데이터를 룬련 데이터(train data)와 평가 데이터(test data)로 나누어 훈련 데이터로 학습시킨 뒤 평가 데이터로 모델을 평가한다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝