미분

함수

함수는 $y=f(x)$와 같이 표기할 수 있는데 y가 x에 따라 결정되는 관계를 뜻한다. 이때 x=a 일때 f(a)가 2개 이상 존재할 수 없다.

평균변화율

• x의 변화량에 따른 y의 변화량의 비율로 함수의 그래프 위의 두 점을 이은 직선의 기울기와 같다.
  
  $\frac{f(b)-f(a)}{b-a}$

순간변화율

• 어느 한 지점에서의 함수의 접선의 기울기이다.
  
  $\displaystyle\lim_{h\rarr0}{\frac{f(a+h)-f(a)}{h}}$

미분

• 함수의 순간변화율을 구하는 방법
  $\dfrac{d}{dx}f(x)$

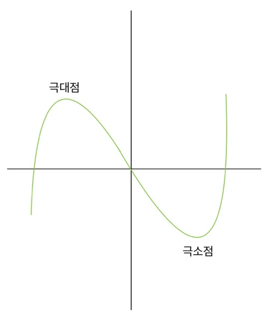
극소, 극대

• 그래프에서 부분적으로 낮은 지점, 부분적으로 높은 지점이다.
• 극점을 기준으로 순간변화율의 부호가 바뀐다.
  • 극소점의 순간변화율 $-$ -> 0 -> $+$
  • 극대점의 순간변화율 $+$ -> 0 -> $-$
• 극소점이 항상 최솟값이 아니고 극대값이 항상 최댓값이 아니라는 것에 유의해야한다.

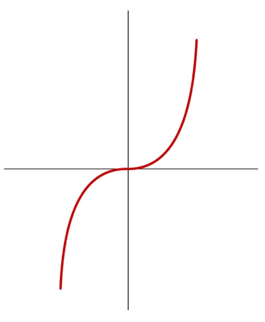
안장점

• 순간변화율이 0이지만 극소도 극대도 아닌 경우
• 순간변화율의 부호가 변하지 않는다.

편미분

• $f(x,y) = x^2 + y^2$ 같은 다변수함수의 경우에는 변수가 많기 때문에 편미분을 한다.
• 편미분은 변수 하나에 대해서만 미분을 하는 것이다.
  • x에 대한 편미분: $f_x = \dfrac{\partial}{\partial x}f(x,y)$
  • y에 대한 편미분: $f_y = \dfrac{\partial}{\partial y}f(x,y)$
• 편미분 결과를 다음과 같이 기울기 벡터로 나타낼 수 있다.
  $\nabla f(x,y) = \begin{bmatrix}f_x\\f_y\\ \end{bmatrix}$

가장 가파른 방향

• 앞서 알아본 기울기 벡터를 통해 특정 지점에서의 기울기를 구할 수 있다.
• $f(x,y) = x^2 + y^2$의 경우 $\nabla f(x,y) = \begin{bmatrix}2x\\2y\\ \end{bmatrix}$이기 때문에 x,y에 변화를 주며 기울기가 최소 또는 최대인 지점을 구할 수 있다.
• 이처럼 다변수 함수의 기울기는 벡터인 것이다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝