다중 선형 회귀

다중 선형 회귀(Multiple Linear Regression)

• 입력변수가 여러 가지인 선형 회귀
• 입력 변수(feature) 여러개 - $x$ / 목표 변수 하나 - $y$

  i 번째 데이터의 j 번째 속성 : $x_j^{(i)}$
  속성이 여러개 이므로 벡터로 나타낸다. $x=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix}$

다중 선형 회귀 가설 함수

　　　　　　　　　　　　$h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n$

　　　　　　　　　　　$\theta = \begin{bmatrix}\theta_0\\\theta_1\\\theta_2\\\vdots\\\theta_n \end{bmatrix}　x=\begin{bmatrix}1\\x_1\\x_2\\\vdots\\x_n \end{bmatrix}$ 　-> 　$h_\theta(x)=\theta^Tx$

다중 선형 회귀에서도 손실 함수는 아래와 같이 선형 회귀와 같다.
$J(\theta) = \displaystyle\frac{1}{2m}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2}$

다중 선형 회귀 경사 하강법

• 다중 선형 회귀는 입력 변수가 여러개이기 때문에 다음과 같이 벡터를 사용하여 $\theta$를 업데이트한다.

　　　　　　　　　　　　　　$X = \begin{bmatrix}x_0^{(1)}&x_1^{(1)}&...&x_n^{(1)}\\x_0^{(2)}&x_1^{(2)}&...&x_n^{(2)}\\\vdots\\x_0^{(m)}&x_1^{(m)}&...&x_n^{(m)}\end{bmatrix}$

　　　　　　　　　　　　　　　$\theta$ <- $\theta - \alpha\displaystyle\frac{1}{m}X^T(X\theta - y)$

$X\theta$가 예측값 이므로 $error = X\theta - y$

정규 방정식(Normal Equation)

　　　　　　　　　　　　　　　　　$\theta(X^TX)^{-1}X^Ty$

• 극소점의 기울기가 0이라는 것을 이용한다.
• 방정식 $\nabla J(\theta) = 0$ 을 통해 최적의 $\theta$를 구한다.
• 시간복잡도 : $O(n^{2.4})$ ~ $O(n^{3})$ (역행렬 구하는 연산)

유사역행렬(pseudoinverse)

　　　　　　　　　　　　　　　　　$X^+$는 $X$의 유사 역행렬

• 정식 명칭은 무어-펜로즈(Moore-Penrose) 역행렬이다.
• 역행렬이 존재하지 않을 경우 사용된다.
• 시간복잡도 : 약 $O(n^{2})$

유사역행렬의 계산
특잇값 분해(SVD - Singular Value Decomposition)를 사용하여 $X^+$를 구한다.
$X = U\Sigma V^T => X^+ = V\Sigma^+ U^T$
알고리즘이 $\Sigma$를 구하고 $\Sigma$에서 어떤 임곗값보다 작은 값을 모두 0으로 치환한 뒤, 0이 아닌 모든 값을 역수로 치환한 다음 전치하여 $\Sigma^+$를 구한다.

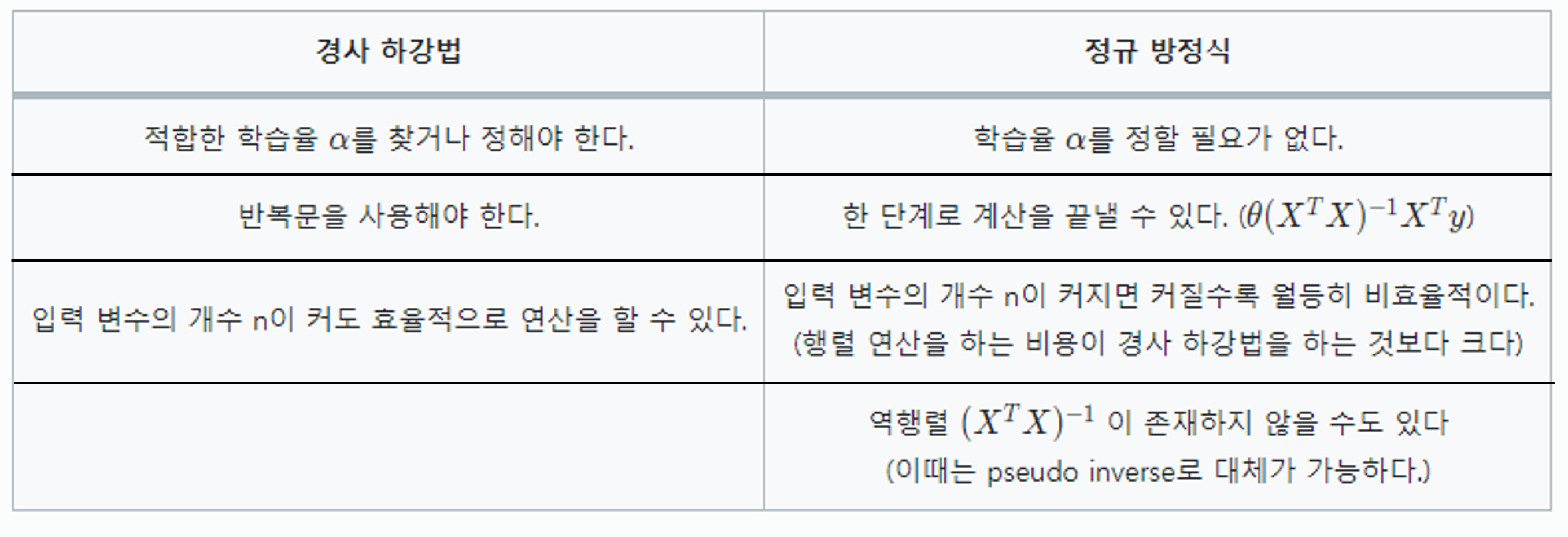
경사 하강법 VS 정규 방정식

• 보통 입력 변수가 많을 때는 경사 하강법, 적을 때는 정규 방정식을 사용한다.(일반적으로 1000개를 기준으로 함)
  

Convex 함수

• 모든 구간에서 아래로 볼록한 함수
• 위로 볼록한 구간이 있는 함수는 non-convex 함수라고 한다.
• 선형 회귀의 손실함수로 사용되는 MSE는 항상 convex 함수이다.

• convex 함수는 항상 하나의 극소점을 가지며 따라서 항상 최소점을 찾을 수 있다.
• non-convex 함수는 구한 극소점이 global minimum이라고 확신할 수 없으므로 local minimum에 빠질 수 있다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝