다항 회귀

이 글은 코드잇 강의를 수강하고 정리한 글입니다. 더 자세한 내용은 코드잇을 참고하세요

코드잇 머신 러닝

다항 회귀(Polynomial Regression)

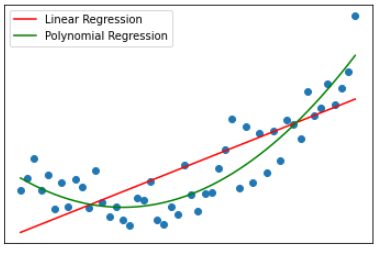
• 데이터에 잘 맞는 일차 함수나 직선을 구하는 게 아니라 다항식이나 곡선을 구해서 학습하는 방법

다항 회귀는 두가지로 나뉜다.

• 속성이 하나인 경우 - 단일 속성 다항 회귀
• 속성이 여러 개인 경우 - 다중 다항 회귀

단일 속성 다항 회귀

• 하나의 입력 변수에 대하여 차수를 확장해 가며 다차원 회귀 모델을 도출한다.
• 입력 변수 $x$를 제곱, 세제곱하여 $x^2, x^3$을 다중 선형 회귀의 $x_2, x_3$처럼 사용한다.
  • 예: $y = ax + b$ - > $y = ax^2 + bx + c$

　　　　　　　　　　　　　$h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + ... + \theta_nx^n$

다중 다항 회귀

• 선형 회귀는 변수들이 독립적이라 변수들 간의 관계를 반영할 수 없다.
• 예: 변수가 $x_1, x_2, x_3$일 때 2차 다중 다항 회귀의 가설 함수($\theta_0$는 상수항):
  $h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_1x_2 + \theta_5x_1x_3 + \theta_6x_2x_3 + \theta_7x_1^2 + \theta_8x_2^2 + \theta_9x_3^2$
  • $x_1x_2$, $x_1x_3$, $x_2x_3$으로 $x_1$, $x_2$, $x_3$간의 관계를 반영할 수 있다.
• 이렇게 추가된 변수를 새로운 변수로 취급하여 다중 선형 회귀처럼 실행하면 다중 다항 회귀를 시행할 수 있다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝