로지스틱 회귀

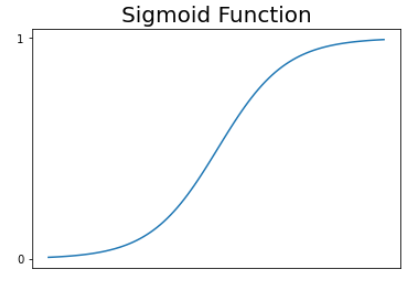
분류 문제에서는 각 결괏값에 숫자 값을 지정해준다.
    예: 꽃의 색이 빨강, 노랑, 보라 -> 빨강: 0, 노랑: 1, 보라: 2
선형 회귀는 이상점(Outlier)에 취약하기 때문에 분류 문제에서는 잘 사용되지 않는다.

로지스틱 회귀(Logistic Regression)

• 지도학습 - 회귀 • 분류
• 데이터에 잘 맞는 시그모이드 함수(Sigmoid Function)를 찾는다.
• 보통 $S(x)$가 0.5보다 큰지 작은지로 분류한다.
• 로지스틱 회귀는 주로 분류에 사용되지만 시그모이드 함수의 값이 0과 1 사이의 연속적인 값이기 때문에 로지스틱 회귀 라고 부른다.

　　　　　　　　　　　　　　　　　　　　$S(x) = \displaystyle\frac{1}{1 + e^{-x}}$

시그모이드 함수의 특성:

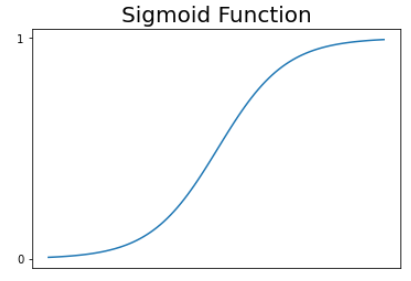
• $0 <= S(x) <= 1$
  -> 값이 0과 1 사이이기 때문에 분류에 적합하다.

로지스틱 회귀 가설 함수

　　　　　　　　　　　　　　$g_\theta(x) = \theta^Tx$　->　$S(\theta^Tx) = h_\theta(x) = \displaystyle\frac{1}{1 + e^{-\theta^Tx}}$

• 1차 함수 $g_\theta(x)$는 치역이 실수 전체이다.
• $g_\theta(x)$를 시그모이드 함수를 통해 $0 <= h_\theta(x) <= 1$이 되도록 한다. (결과 범위를 제한한다.)
• $\theta$가 가설 함수에 미치는 영향: $x$축 이동, 기울기 변화 등

로지스틱 가설 함수의 의미:

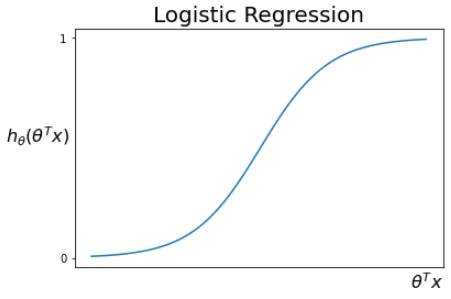
• 통과를 1, 실패를 0으로 했을 때 $h_\theta(x) = 0.8$이면 통과할 확률이 80%라는 뜻이다.
• 따라서 0.5를 기준으로 통과, 실패를 분류할 수 있다.
• 시그모이드 함수에 $\theta^Tx$(선형 회귀의 가설 함수)가 변수로 들어가기 때문에 선형 회귀에 한 단계가 추가된 방법이라고 생각할 수도 있다.

결정 경계(Decision Boundary)

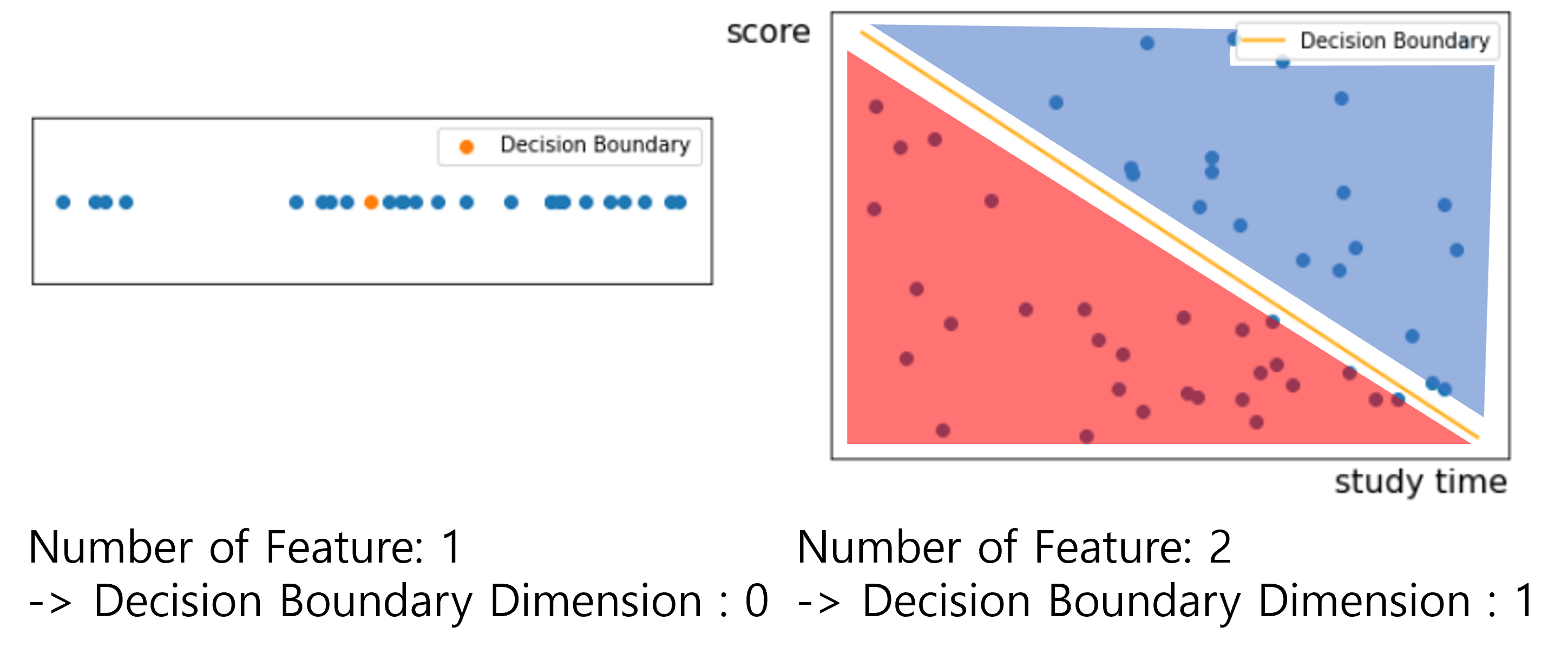
• 분류 문제에서 결과를 나누는 경계를 결정 경계라고 한다.
• N차원을 둘로 나누려면 N-1차원이 필요하다.
  • 속성이 1개이면 결정 경계는 0차원
  • 속성이 2개이면 결정 경계는 1차원

로그 손실(Log loss / Cross entropy)

　　　　　　　　　$logloss(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))$

아래의 식은 위의 식과 같은 식이지만 보통 위의 방식으로 단위 계단 함수를 사용하여 나타내는 것이 일반적이다.
$logloss(h_\theta(x),y) = \begin{cases} -log(h_\theta(x))\,　　　y=1\\ -log(1-h_\theta(x))\,\,\,　y=0 \end{cases}$

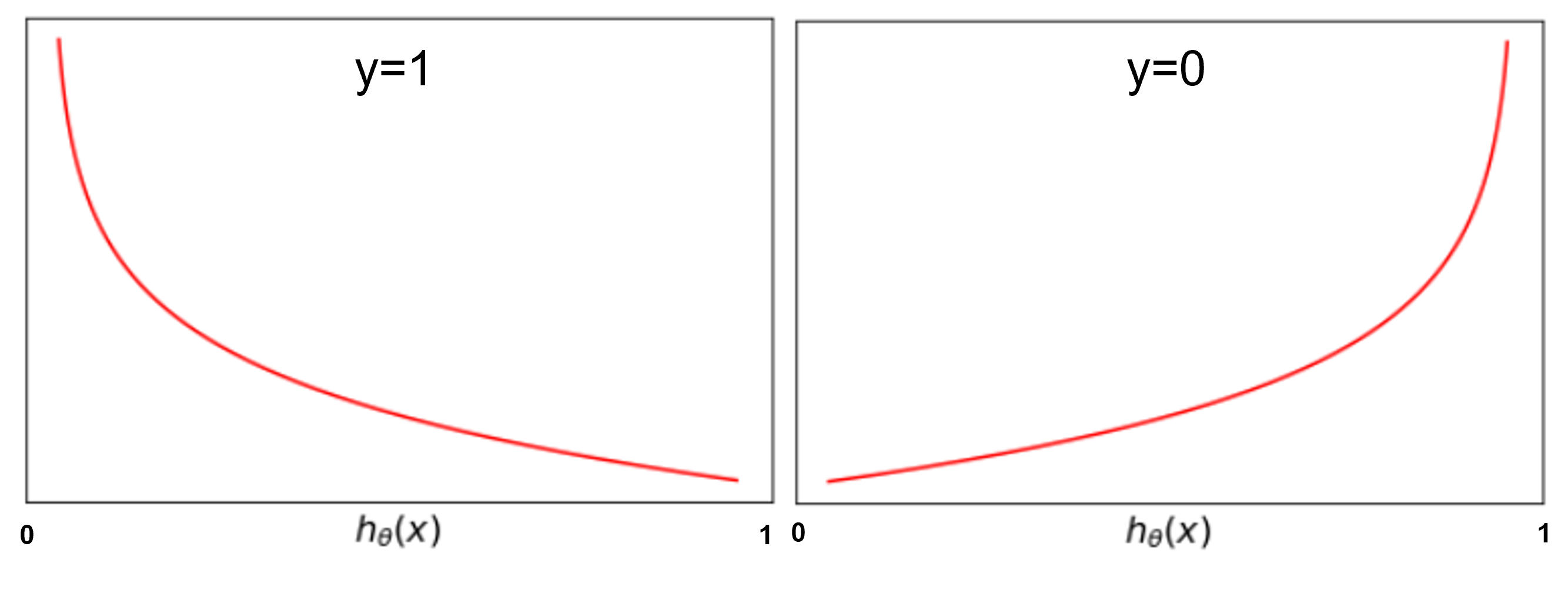
• 손실의 정도를 로그 함수로 나타낸다.
• $y=1$인 경우 $h_\theta(x)$가 1에서 멀어질수록 손실을 키운다.
• $y=0$인 경우 $h_\theta(x)$가 0에서 멀어질수록 손실을 키운다.

로지스틱 회귀에서 MSE(mean squared error)를 사용하지 않는 이유:

• error가 0~1 사이의 값이어서 제곱을 하면 매우 작아 의미가 없어진다.
  $\rightarrow$ 로그손실 함수를 사용해서 패널티를 키운다.
• 로지스틱 회귀에서 MSE를 사용하면 미분결과가 convex 하지 않아 사용 불가능하다.

로지스틱 회귀 손실 함수

　　　　　　　　　　　　　　　$J(\theta) = \displaystyle\frac{1}{m}\sum_{i=1}^m{logloss(h_\theta(x^{(i)}),y^{(i)})}$

• 데이터의 로그 손실의 평균

로지스틱 회귀 경사 하강법

　　　　　　　　　$\theta_j = \theta_j - \alpha\displaystyle\frac{\partial}{\partial\theta_j}J(\theta) = \theta_j = \theta_j - \alpha\displaystyle\frac{1}{m}\sum_{i=1}^m{(h_\theta(x^{(i)}) - y^{(i)})\,·\,x_j^{(i)}}$

• 선형 회귀의 경사 하강법과 같지만 $h_\theta(x)$가 다르다.
  • $h_\theta(x) = \displaystyle\frac{1}{1 + e^{-\theta^Tx}}$ (시그모이드 함수)

　　　　　　　　　　　　　　　　$\theta \leftarrow \theta - \alpha\displaystyle\frac{1}{m}X^T \times error$

앞서 언급한 것처럼 로지스틱 회귀의 예측결과는 선형회귀 결과를 시그모이드 함수에 대입한 값과 같으므로

• 예측 결과: $sigmoid(X\theta)$
• $error = sigmoid(X\theta)-y$

로지스틱 회귀 다중 분류

• 클래스가 3개 이상인 경우
• 각 클래스에 대한 로지스틱 회귀를 진행한 후 확률이 가장 높은 클래스로 예측한다.
  예: 클래스가 $A, B, C$가 있을 때 ($h_\theta^{(j)}(x)$는 j번째 클래스일 확률을 구하는 함수)
  • $A$일 확률을 리턴하는 함수 $h_\theta^{(0)}(x)$ = 0.37
  • $B$일 확률을 리턴하는 함수 $h_\theta^{(1)}(x)$ = 0.23
  • $C$일 확률을 리턴하는 함수 $h_\theta^{(2)}(x)$ = 0.62
    이면 $C$로 예측한다.

소프트맥스 함수(Softmax Function)

• 다중 분류시에 각 클래스별 확률을 의미 있는 결과로 변환하기 위해 사용하는 함수이다.
• 확률의 총합은 1인데 위 예시의 경우 확률의 합이 1이 되지 않는다. 따라서 위의 확률을 그대로 사용하기는 힘들다. $\leftarrow$ 이러한 경우에 사용된다.
  $p_j = \displaystyle\frac{h_\theta^{(j)}(x)}{\sum_{k=1}^K{h_\theta^{(k)}(x)}}$ ($K$는 클래스의 수)
  

로지스틱 회귀 정규방정식

• 로지스틱 회귀의 손실함수 $J(\theta)$는 convex 함수이지만, $J(\theta)$의 편미분 대상($\theta$항)들이 선형적이지 않아서 정규방정식 사용이 불가능하다.

이 글은 코드잇 강의를 수강하며 정리한 글입니다. 더 자세한 설명은 코드잇을 참고하세요

코드잇 머신 러닝