그래프

그래프는 노드와 에지로 구성된 집합이다. 노드는 데이터를 표현하는 단위이고 에지는 노드를 연결한다. 그래프는 여러 알고리즘에 많이 사용되는 자료구조이므로 코딩테스트에 자주 등장하니 집중해서 공부해야 할 필요가 있다.

08-1 그래프의 표현

2차원 리스트 생성

0으로 초기화한 행(row) 개수 3, 열(column) 개수 4인 2차원 리스트를 생성할 때는 어떻게 해야 할까?

• 리스트를 객체로 생성하는 방법(추천)
  A = [[0 for col in range(4)] for row in range(3)]

• 얕은 복사를 일으켜 생성하는 방법
  A = [[0]*4]*3]
  //이와 같은 방식으로 선언한 후 값을 변경하면 다른 원소의 값도 함께 변경될 수 있다.

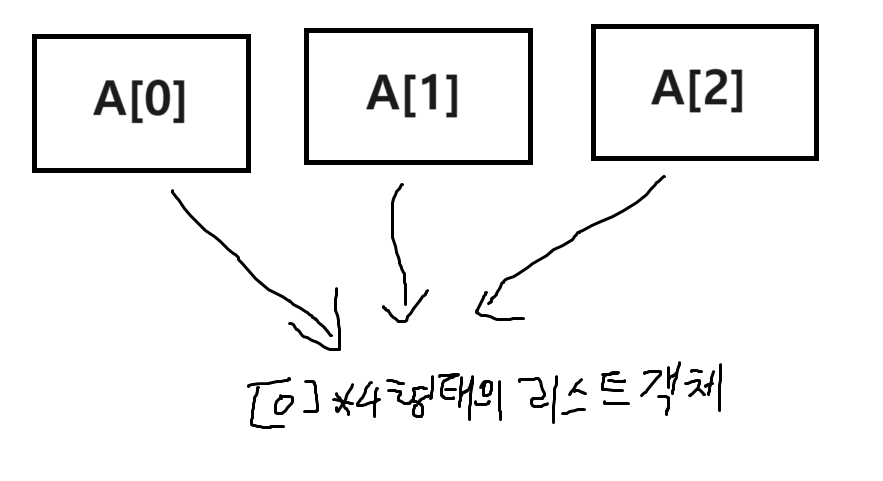
<2차원 리스트 생성에서 얕은 복사 동작 원리>
A = [[0]4]3에서 [0]*4의 형태의 리스트 객체를 1개를 생성하고 모든 리스트(3개)의 각 요소가 해당 객체를 바라본다.

위와 같은 원리가 작용하여 A[0][0]의 값을 1로 변경하면 A[1][0], A[2][0]도 함께 변경되므로 첫번째 선언 방식으로 생성해야 한다.

에지 리스트

에지 리스트는 에지를 중심으로 그래프를 표현한다. 에지 리스트는 리스트에 출발 노드, 도착 노드를 저장하여 에지를 표현한다. 또는 출발 노드, 도착 노드, 가중치를 저장하여 가중치가 이쓴ㄴ 에지를 표현한다.

에지 리스트(가중치x)

가중치가 없는 그래프는 출발 노드와 도착 노드만 표현하므로 리스트의 열은 2개면 충분하다.

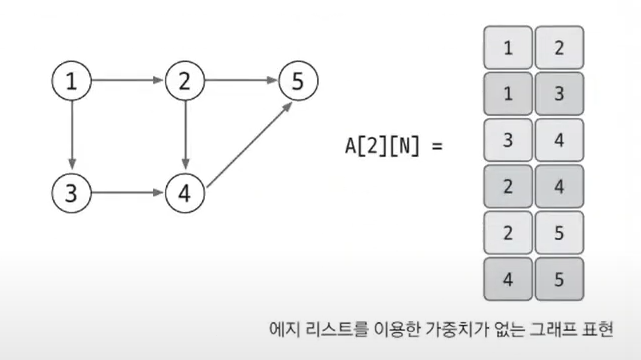
1에서 2로 뻗어나가는 에지는 [1, 2]로 표현한다. 4에서 5로 뻗어나가는 에지는 [4, 5]로 표현한다. 이처럼 방향이 있는 그래프는 순서에 맞게 노드를 리스트에 저장하는 방식으로 표현한다. 그리고 노드를 리스트에 저장하여 에지를 표현하므로 에지 리스트라고 한다. 여기서 만약 방향이 없는 그래프라면 [1, 2], [2, 1]는 같은 표현이다.

에지 리스트(가중치o)

가중치가 있는 그래프는 열을 3개로 늘려 3번째 열에 가중치를 저장하면 된다.

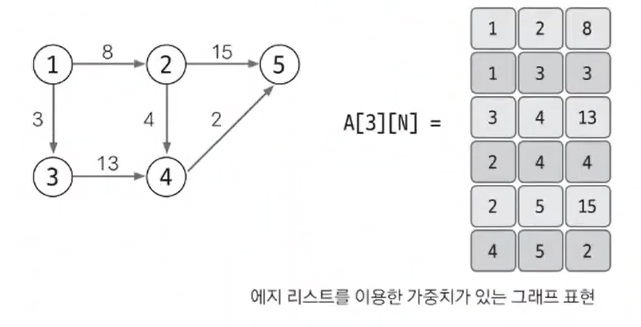
1에서 2로 향하는 가중치가 8인 에지는 이제 [1, 2, 8]로 표현한다. 이처럼 에지 리스트는 구현하기 쉽다. 하지만 특정 노드와 관련되어 있는 에지를 탐색하기는 쉽지 않ㄴ다. 에지 리스트는 노드 사이의 최단 거리를 구하는 벨만-포드나 최소 신장 트리를 찾는 크루스칼 알고리즘에 사용하며, 노드 중심 알고리즘에는 잘 사용하지 않는다.

인접 행렬

인접 행렬은 2차원 리스트를 자료구조로 이용하여 그래프를 표현한다. 인접 행렬은 에지 리스트와 다르게 노드 중심으로 그래프를 표현한다.

인접 행렬로 가중치 없는 그래프 표현하기

다음 그림을 보면 1에서 2를 향하는 에지를 인접 행렬은 1행 2열에 1을 저장하는 방식으로 표현한다. 1을 저장하는 이유는 가중ㅇ치가 없기 때문이다("있다"는 의미의 1). 1에서 2로 향하는 에지가 있다는 표시를 노드 중심으로 이해하자.

인접 행렬로 가중치 있는 그래프 표현하기

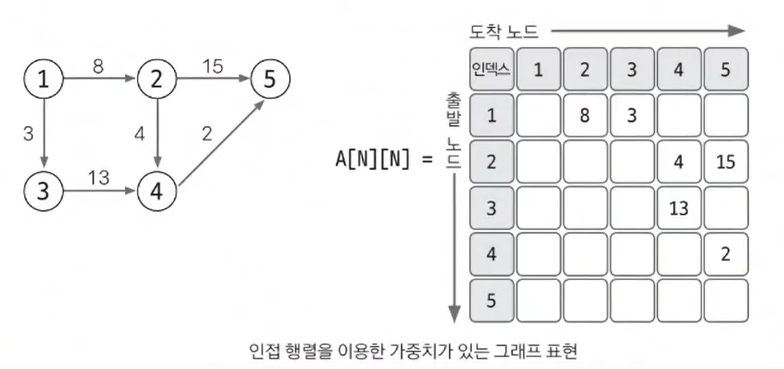
인접 행렬의 가중치는 매우 직관적이다. 1대신 가중치 값을 초기화하면 된다. 이처럼 인접 행렬을 이용한 그래프 구현은 쉽다. 두 노드를 연결하는 에지의 여부와 가중치값은 리스트에 직접 접근하면 바로 확인할 수 있다는 것도 장점이다. 하지만 노드와 관현되어 있는 에지를 탐색하려면 N번 접근해야 하므로 시간 복잡도가 인접 리스트에 비해 느리고 노드 개수에 비해 에지가 적을 때는 공간 효율성이 떨어진다. 따라서 N이 작을 때만 인접 행렬을 사용하는 것이 현명하게 문제를 접근하는 것이다.

인접 리스트(중요)

인접 리스트는 파이썬의 리스트를 이용하여 그래프를 표현한다. 노드 개수만큼 리스트를 선언한다. 리스트의 input data 형태는 문제의 조건에 맞게 설정한다.

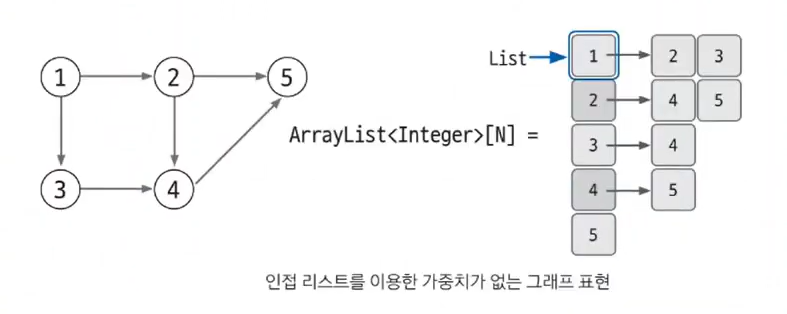
인접 리스트로 가중치 없는 그래프 표현하기

다음은 인접 리스트를 가중치 없는 그래프를 표현한 것이다. 현재의 경우 int 데이터 하나로 그래프를 표현하기에 충분하다. 인접 리스트에는 N번 노드와 연결되어 있는 노드를 리스트의 index N에 연결된 노드 개수만큼 리스트에 append하는 방식으로 표현한다.

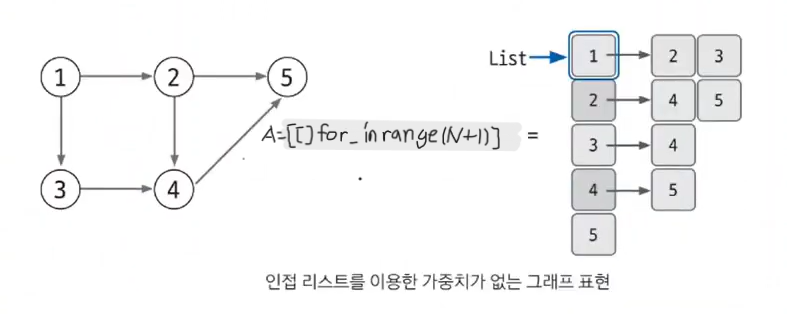
예를 들어 노드 1과 연결된 2, 3노드는 A[1]에 [2, 3]을 연결하는 방식으로 표현한다.

인접 리스트로 가중치 있는 그래프 표현하기(중요)

가중치가 있는 경우 input data를 2개(도착 노드, 가중치)로 사용한다.

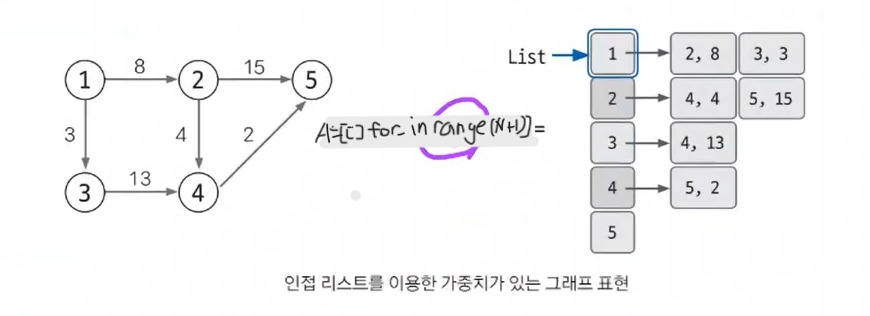
그림을 보면 A[1]에 [(2, 8), (3, 3)]이 연결되어 있다. 이는 노드 1과 2가 가중치 8 에지로, 노드 1과 3이 가중치 3 에지로 연결되어 있다는 것을 보영준다. 방향성도 고려되었다. 그래프를 구현하는 다른 방법에 비해 인접 리스트를 이용한 그래프 구현은 복잡한 편이다. 하지만 노드와 연결된 에지를 탐색하는 시간은 매우 뛰어나며, 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러도 발생하지 않는다. 이런 장점으로 실제 코테에선 인접리스트를 이용한 그래프 구현이 가장 빈번하다.